tikz中谐振子（弹簧）的绘制，以及声子色散关系的绘制

今天整理了简正模导出声子的内容，其中用tikz画了两张图。一张是整个问题的物理模型，效果如下

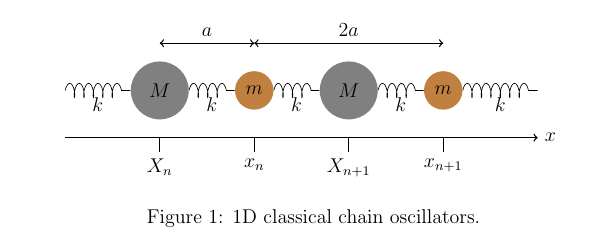
这幅图的绘制参考了https://tex.stackexchange.com/questions/41608/draw-mechanical-springs-in-tikz中弹簧的绘制。具体代码如下：

\usepackage{tikz}
\usepackage{pgfplots}
\usetikzlibrary{decorations.pathmorphing,patterns}

\begin{figure}\label{classical chain}
\centering
\begin{tikzpicture}
	\node[circle,fill=gray,inner sep=2.5mm] (a1) at (2,0){$M$};
	\node[circle,fill=brown,inner sep=1.5mm] (b1) at (4,0){$m$};
	\node[circle,fill=gray,inner sep=2.5mm] (a2) at (6,0){$M$};
	\node[circle,fill=brown,inner sep=1.5mm] (b2) at (8,0){$m$};
	\draw[decoration={aspect=0.3, segment length=2mm, amplitude=1.5mm,coil},decorate](0,0)--(a1) node[midway,below]{$k$};
	\draw[decoration={aspect=0.3, segment length=2mm, amplitude=1.5mm,coil},decorate](a1)--(b1)node[midway,below]{$k$};
	\draw[decoration={aspect=0.3, segment length=2mm, amplitude=1.5mm,coil},decorate](b1)--(a2)node[midway,below]{$k$};
	\draw[decoration={aspect=0.3, segment length=2mm, amplitude=1.5mm,coil},decorate](a2)--(b2)node[midway,below]{$k$};
	\draw[decoration={aspect=0.3, segment length=2mm, amplitude=1.5mm,coil},decorate](b2)--(10,0)node[midway,below]{$k$};
	\draw[->,thick](0,-1)--(10,-1) node[right]{$x$};
	\draw (2,-1)--(2,-1.3) node[anchor=north]{$X_n$};
	\draw (4,-1)--(4,-1.3) node[anchor=north]{$x_n$};
	\draw (6,-1)--(6,-1.3) node[anchor=north]{$X_{n+1}$};
	\draw (8,-1)--(8,-1.3) node[anchor=north]{$x_{n+1}$};
	\draw [<->,thick](2,1)--(4,1) node[midway,above]{$a$};
	\draw [<->,thick](4,1)--(8,1) node[midway,above]{$2a$};
\end{tikzpicture}
\caption{1D classical chain oscillators.}
\end{figure}

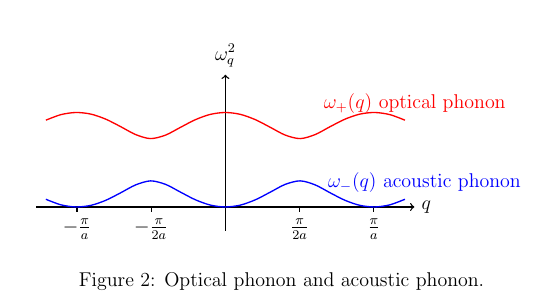
声子的色散关系是tikz中函数关系的绘制，代码如下：

\begin{figure}\label{phonon}
\centering
\begin{tikzpicture}
	\draw[->,thick](-4,0)--(4,0) node[right]{$q$};
	\draw[->,thick](0,-0.5)--(0,2.8) node[above]{$\omega_q^2$};
	\draw[-,thick](-pi/2,0)--(-pi/2,-0.1) node[below]{$-\frac{\pi}{2a}$};
	\draw[-,thick](pi/2,0)--(pi/2,-0.1) node[below]{$\frac{\pi}{2a}$};
	\draw[-,thick](-pi,0)--(-pi,-0.1) node[below]{$-\frac{\pi}{a}$};
	\draw[-,thick](pi,0)--(pi,-0.1) node[below]{$\frac{\pi}{a}$};

	\draw [red,domain=-3.8:3.8,smooth,thick] plot (\x, {1+sqrt(1-0.8*sin(\x r)*sin(\x r))}) node[above]{$\quad\omega_+(q)$ optical phonon};
	\draw [blue,domain=-3.8:3.8,smooth,thick] plot (\x, {1-sqrt(1-0.8*sin(\x r)*sin(\x r))}) node[above]{$\qquad \omega_-(q)$ acoustic phonon};
\end{tikzpicture}
\caption{Optical phonon and acoustic phonon.}
\end{figure}

结果如下：