普里姆Prim算法介绍

普里姆(Prim)算法，和克鲁斯卡尔算法一样，是用来求加权连通图的最小生成树的算法。

基本思想 
对于图G而言，V是所有顶点的集合；现在，设置两个新的集合U和T，其中U用于存放G的最小生成树中的顶点，T存放G的最小生成树中的边。
从所有uЄU，vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v)，将顶点v加入集合U中，将边(u,
v)加入集合T中，如此不断重复，直到U=V为止，最小生成树构造完毕，这时集合T中包含了最小生成树中的所有边。

普里姆算法图解

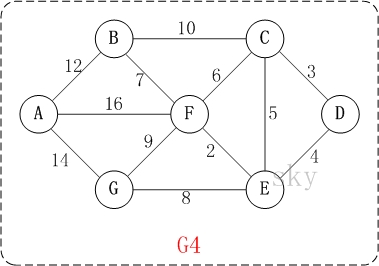
以上图G4为例，来对普里姆进行演示(从第一个顶点A开始通过普里姆算法生成最小生成树)。

初始状态：V是所有顶点的集合，即V={A,B,C,D,E,F,G}；U和T都是空！ 
第1步：将顶点A加入到U中。 
    此时，U={A}。 
第2步：将顶点B加入到U中。 
    上一步操作之后，U={A}, V-U={B,C,D,E,F,G}；因此，边(A,B)的权值最小。将顶点B添加到U中；此时，U={A,B}。 
第3步：将顶点F加入到U中。 
    上一步操作之后，U={A,B}, V-U={C,D,E,F,G}；因此，边(B,F)的权值最小。将顶点F添加到U中；此时，U={A,B,F}。 
第4步：将顶点E加入到U中。 
    上一步操作之后，U={A,B,F}, V-U={C,D,E,G}；因此，边(F,E)的权值最小。将顶点E添加到U中；此时，U={A,B,F,E}。 
第5步：将顶点D加入到U中。 
    上一步操作之后，U={A,B,F,E}, V-U={C,D,G}；因此，边(E,D)的权值最小。将顶点D添加到U中；此时，U={A,B,F,E,D}。 
第6步：将顶点C加入到U中。 
    上一步操作之后，U={A,B,F,E,D}, V-U={C,G}；因此，边(D,C)的权值最小。将顶点C添加到U中；此时，U={A,B,F,E,D,C}。 
第7步：将顶点G加入到U中。 
    上一步操作之后，U={A,B,F,E,D,C}, V-U={G}；因此，边(E,G)的权值最小。将顶点G添加到U中；此时，U=V。

此时，最小生成树构造完成！它包括的顶点依次是：A B F E D C G。

普里姆算法的代码说明

以"邻接矩阵"为例对普里姆算法进行说明，对于"邻接表"实现的图在后面会给出相应的源码。

1. 基本定义

// 邻接矩阵
typedef struct _graph
{
    char vexs[MAX];       // 顶点集合
    int vexnum;           // 顶点数
    int edgnum;           // 边数
    int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;

// 边的结构体
typedef struct _EdgeData
{
    char start; // 边的起点
    char end;   // 边的终点
    int weight; // 边的权重
}EData;

Graph是邻接矩阵对应的结构体。 
vexs用于保存顶点，vexnum是顶点数，edgnum是边数；matrix则是用于保存矩阵信息的二维数组。例如，matrix[i][j]=1，则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点；matrix[i][j]=0，则表示它们不是邻接点。 
EData是邻接矩阵边对应的结构体。

2. 普里姆算法

#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
#define MAX 100
#define INF (~(0x1<<31))
typedef struct Graph
{
    char vexs[MAX];
    int vexnum;
    int edgnum;
    int matrix[MAX][MAX];
} Graph,*PGraph;

typedef struct EdgeData
{
    char start;
    char end;
    int weight;
} EData;

static int get_position(Graph g,char ch)
{
    int i;
    for(i=0; i<g.vexnum; i++)
        if(g.vexs[i]==ch)
            return i;
    return -1;
}

Graph* create_graph()
{
    char vexs[]= {'A','B','C','D','E','F','G'};
    int matrix[][7]=
    {
        {0,12,INF,INF,INF,16,14},
        {12,0,10,INF,INF,7,INF},
        {INF,10,0,3,5,6,INF},
        {INF,INF,3,0,4,INF,INF},
        {INF,INF,5,4,0,INF,8},
        {16,7,6,INF,2,0,9},
        {14,INF,INF,INF,8,9,0}
    };
    int vlen=sizeof(vexs)/sizeof(vexs[0]);
    int i,j;
    Graph *pG;
    if((pG=(Graph*)malloc(sizeof(Graph)))==NULL)
        return NULL;
    memset(pG,0,sizeof(pG));
    pG->vexnum=vlen;
    for(i=0; i<pG->vexnum; i++)
        pG->vexs[i]=vexs[i];
    for(i=0; i<pG->vexnum; i++)
        for(j=0; j<pG->vexnum; j++)
            pG->matrix[i][j]=matrix[i][j];
    for(i=0; i<pG->vexnum; i++)
    {
        for(j=0; j<pG->vexnum; j++)
        {
            if(i!=j&&pG->matrix[i][j]!=INF)
                pG->edgnum++;
        }
    }
    pG->edgnum/=2;
    return pG;
}

void print_graph(Graph G)
{
    int i,j;
    printf("Matrix Graph: \n");
    for(i=0; i<G.vexnum; i++)
    {
        for(j=0; j<G.vexnum; j++)
            printf("%10d ",G.matrix[i][j]);
        printf("\n");
    }
}

EData* get_edges(Graph G)
{
    EData *edges;
    edges=(EData*)malloc(G.edgnum*sizeof(EData));
    int i,j;
    int index=0;
    for(i=0; i<G.vexnum; i++)
    {
        for(j=i+1; j<G.vexnum; j++)
        {
            if(G.matrix[i][j]!=INF)
            {
                edges[index].start=G.vexs[i];
                edges[index].end=G.vexs[j];
                edges[index].weight=G.matrix[i][j];
                index++;
            }
        }
    }
    return edges;
}

void prim(Graph G,int start)
{
    int min,i,j,k,m,n,sum;
    int index=0;
    char prim[MAX];
    int weight[MAX];

    prim[index++]=G.vexs[start];

    for(i=0; i<G.vexnum; i++)
        weight[i]=G.matrix[start][i];
    weight[start]=0;

    for(i=0; i<G.vexnum; i++)
    {
       //i用来控制循环的次数，每次加入一个结点，但是因为start已经加入，所以当i为start是跳过
        if(start==i)
            continue;
        j=0;
        k=0;
        min=INF;
        for(k=0; k<G.vexnum; k++)
        {
            if(weight[k]&&weight[k]<min)
            {
                min=weight[k];
                j=k;
            }
        }
        sum+=min;
        prim[index++]=G.vexs[j];
        weight[j]=0;
        for(k=0; k<G.vexnum; k++)
        {
            if(weight[k]&&G.matrix[j][k]<weight[k])
                weight[k]=G.matrix[j][k];
        }
    }
    // 计算最小生成树的权值
    sum = 0;
    for (i = 1; i < index; i++)
    {
        min = INF;
        // 获取prims[i]在G中的位置
        n = get_position(G, prim[i]);
        // 在vexs[0...i]中，找出到j的权值最小的顶点。
        for (j = 0; j < i; j++)
        {
            m = get_position(G, prim[j]);
            if (G.matrix[m][n]<min)
                min = G.matrix[m][n];
        }
        sum += min;
    }
    printf("PRIM(%c)=%d: ", G.vexs[start], sum);
    for (i = 0; i < index; i++)
        printf("%c ", prim[i]);
    printf("\n");
}

int main()
{
    Graph *pG;
    pG=create_graph();
    print_graph(*pG);
    prim(*pG,0);
}

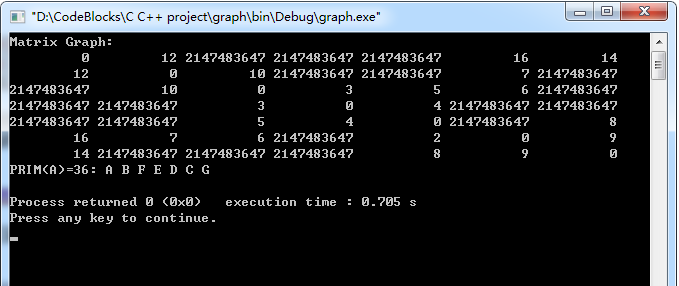
运行结果：