bzoj3672: [Noi2014]购票（树形DP+斜率优化+可持久化凸包）

　　这题的加强版，多了一个$l_i$的限制，少了一个$p_i$的单调性，难了好多...

　　首先有方程$f(i)=min\{f(j)+(dep_i-dep_j)*p_i+q_i\}$

　　$\frac {f(j)-f(k)}{dep_j-dep_k}<p_i$

　　假如没有$l_i$的限制，实际上就是上面那题...

　　如果多了$l_i$的限制会有什么影响呢？

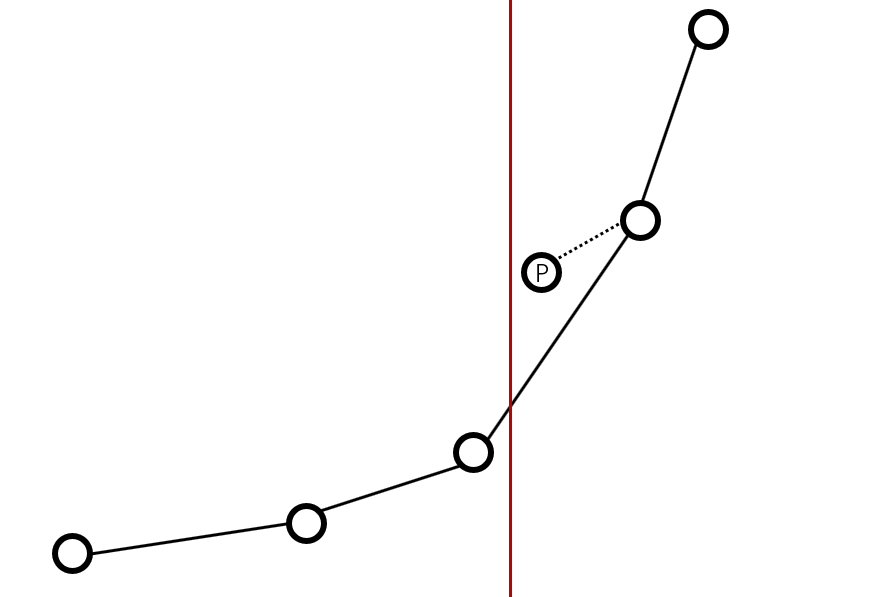
　　类似上图的情况...红线是$l_i$的限制，如果是单调队列写法的话，P点会被删掉，但实际上P点依然有可能成为最优决策点...

　　这个时候一个单调队列的写法就不可行了...

　　之所以会出现这个问题，是因为P点被不属于$l_i$范围内的点给弹出了，所以我们只能在不存在$l_i$之外的点的单调队列里查，但是这样我们要开$O(n)$个队列，显然无法承受，但是我们知道的是，凸包是可以合并的，所以直接用线段树来维护就好了。

　　我们需要维护$2n$个队列，像线段树一样，分别维护深度为$[1,dep],[1,dep/2],[dep/2+1,dep],[1,dep/4],[dep/4+1,dep/2],...$的单调队列，每次询问的时候把在距离范围内的区间一个一个合并起来，每个区间都需要二分$O(logn)$找出最优决策点，最后合并$O(logn)$个区间，合并的时候只需要求出一个各个区间最优决策点的凸包就好了，每次合并$O(1)$，复杂度$O(nlog^2n)$。

　　修改的话同理，把包含当前点的所有区间都二分找到出队位置移动队尾位置，同时记录下被覆盖的点，维护一下可持久化凸包，然后就可以了，这一部分细节比较多，结合代码更好理解。

　　队列数组开小+很多地方没开LL+困=调了1h，第一次编译的时候代码就没有实质上的错误了，但是却调了那么久，sigh...

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#define ll long long
#define int long long
using namespace std;
const int maxn=, inf=1e9;
struct poi{int too, dis, pre;}e[maxn];
struct tjm{int bg, len;}tree[maxn<<];
int n, m, x, z, tot, sum;
int v[maxn*], last[maxn], p[maxn], l[maxn], memv[maxn][], meml[maxn][];
ll f[maxn], dep[maxn], deep[maxn], q[maxn];
inline void read(int &k)
{
    int f=; k=; char c=getchar();
    while(c<'' || c>'') c=='-'&&(f=-), c=getchar();
    while(c<='' && c>='') k=k*+c-'', c=getchar();
    k*=f;
}
inline void add(int x, int y, int z){e[++tot]=(poi){y, z, last[x]}; last[x]=tot;}
inline double xl(int x, int y){return 1.0*(f[x]-f[y])/(deep[x]-deep[y]);}
inline int findans(int l, int r, ll limit)
{
    if(l>=r) return r;
    int L=l+, R=r;
    while(L<R)
    {
        int mid=(L+R)>>;
        if(limit-xl(v[mid], v[mid-])>1e-) L=mid+;
        else R=mid;
    }
    if(xl(v[L], v[L-])>=limit) L--;
    return L;
}
inline int find(int r, int limit)
{
    int L=, R=r;
    while(L<R)
    {
        int mid=(L+R)>>;
        if(dep[mid]>=limit) R=mid;
        else L=mid+;
    }
    return L;
}
inline int findr(int l, int r, int pos)
{
    if(l>=r) return r;
    int L=l+, R=r;
    while(L<R)
    {
        int mid=(L+R+)>>;
        if(xl(v[mid], v[mid-])-xl(v[mid], pos)>1e-) R=mid-;
        else L=mid;
    }
    if(xl(v[L], v[L-])-xl(v[L], pos)>1e-) L--;
    return L;
}
void build(int x, int l, int r)
{
    tree[x].bg=sum; sum+=r-l+;
    if(l==r) return;
    int mid=(l+r)>>;
    build(x<<, l, mid); build(x<<|, mid+, r);
}
int query(int x, int l, int r, int cx, ll limit)
{
    if(!tree[x].len || r<cx) return -;
    if(cx<=l) return findans(tree[x].bg, tree[x].bg+tree[x].len-, limit);
    int mid=(l+r)>>, lt=query(x<<, l, mid, cx, limit), rt=query(x<<|, mid+, r, cx, limit);
    if(lt!=- && rt!=-) if(limit-xl(v[lt], v[rt])>1e-) swap(lt, rt);
    return lt==-?rt:lt;
}
void update(int x, int l, int r, int cx, int pos, int d)
{
    int R=findr(tree[x].bg, tree[x].bg+tree[x].len-, pos);
    memv[pos][d]=v[++R]; meml[pos][d]=tree[x].len; v[R]=pos; tree[x].len=R-tree[x].bg+;
    if(l==r) return;
    int mid=(l+r)>>;
    if(cx<=mid) update(x<<, l, mid, cx, pos, d+);
    else update(x<<|, mid+, r, cx, pos, d+);
}
void recovey(int x, int l, int r, int cx, int pos, int d)
{
    v[tree[x].bg+tree[x].len-]=memv[pos][d]; tree[x].len=meml[pos][d];
    if(l==r) return;
    int mid=(l+r)>>;
    if(cx<=mid) recovey(x<<, l, mid, cx, pos, d+);
    else recovey(x<<|, mid+, r, cx, pos, d+);
}
void dfs(int x, int d)
{
    if(x!=)
    {
        int limit=dep[d]-l[x], nxt=v[query(, , n, find(d-, limit), p[x])];
        f[x]=f[nxt]+(deep[x]-deep[nxt])*p[x]+q[x];
    }
    update(, , n, d, x, );
    for(int i=last[x], too;i;i=e[i].pre)
    deep[too=e[i].too]=deep[x]+e[i].dis, dep[d+]=dep[d]+e[i].dis, dfs(too, d+);
    recovey(, , n, d, x, );
}
#undef int
int main()
{
    read(n); read(m);
    for(int i=;i<=n;i++)
        read(x), read(z), read(p[i]), read(q[i]), read(l[i]), add(x, i, z);
    sum=; build(, , n); dfs(, );
    for(int i=;i<=n;i++) printf("%lld\n", f[i]);
}