【费用流】【网络流24题】【P4013】 数字梯形问题

Description

给定一个由 \(n\) 行数字组成的数字梯形如下图所示。

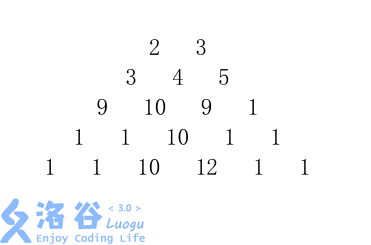
梯形的第一行有 \(m\) 个数字。从梯形的顶部的 \(m\) 个数字开始，在每个数字处可以沿左下或右下方向移动，形成一条从梯形的顶至底的路径。

分别遵守以下规则：

1. 从梯形的顶至底的 \(m\) 条路径互不相交；
2. 从梯形的顶至底的 \(m\) 条路径仅在数字结点处相交；
3. 从梯形的顶至底的 \(m\) 条路径允许在数字结点相交或边相交。

Limitation

\(1~\leq~n,~m~\leq~20\)

Solution

解释一下题意，边不相交指的是不能有两条路径同时经过 \(u \rightarrow~v\) 的路径。

先考虑限制 \(3\)，也就是没有限制的情况，做法非常显然，上一层向下一层的数字连边，容量为无穷代表这条边可以走无穷次，花费为 \(0\)。每个数字都拆一下点，两个点之间连边容量为无穷，代表可以选这个点无数次，花费为这个点的权值代表经过他付出的代价，\(s\) 向第一层连容量为 \(1\) 费用为 \(0\) 的边，最后一层向 \(t\) 连容量为无穷费用为 \(0\) 的边，跑最大费用最大流即可。

考虑限制 \(2\)，一条边只能经过一次，于是将边的容量置为 \(1\) 即可。

考虑限制 \(1\)，同理将点的容量置成 \(1\) 即可。

然后如果你Wa前两个点需要注意梯形的最下面会有 \(n + m\) 个点而不是 \(m\) 个

Code

#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#ifdef ONLINE_JUDGE
#define freopen(a, b, c)
#endif

typedef long long int ll;

namespace IPT {
  const int L = 1000000;
  char buf[L], *front=buf, *end=buf;
  char GetChar() {
    if (front == end) {
      end = buf + fread(front = buf, 1, L, stdin);
      if (front == end) return -1;
    }
    return *(front++);
  }
}

template <typename T>
inline void qr(T &x) {
  char ch = IPT::GetChar(), lst = ' ';
  while ((ch > '9') || (ch < '0')) lst = ch, ch=IPT::GetChar();
  while ((ch >= '0') && (ch <= '9')) x = (x << 1) + (x << 3) + (ch ^ 48), ch = IPT::GetChar();
  if (lst == '-') x = -x;
}

namespace OPT {
  char buf[120];
}

template <typename T>
inline void qw(T x, const char aft, const bool pt) {
  if (x < 0) {x = -x, putchar('-');}
  int top=0;
  do {OPT::buf[++top] = static_cast<char>(x % 10 + '0');} while (x /= 10);
  while (top) putchar(OPT::buf[top--]);
  if (pt) putchar(aft);
}

const int maxn = 5010;
const int INF = 0x3f3f3f3f;

struct Edge {
  int u, v, flow, fee;
  Edge *nxt, *bk;
  Edge(const int _u, const int _v, const int _flow, const int _fee, Edge* &h)
      : u(_u), v(_v), flow(_flow), fee(_fee), nxt(h) {
    h = this;
  }

  ~Edge() {
    if (this->nxt) delete this->nxt;
  }
};
Edge *hd[maxn], *pre[maxn];
inline void cont(const int _u, const int _v, const int _flow, const int _fee) {
  auto u = new Edge(_u, _v, _flow, _fee, hd[_u]), v = new Edge(_v, _u, 0, -_fee, hd[_v]);
  (u->bk = v)->bk = u;
}

int n, m, s, t, ans;
int MU[maxn][maxn], id[maxn][maxn][2], dist[maxn], canag[maxn];
bool inq[maxn];
std::queue<int>Q;

void EK();
bool spfa();
void argu();
void setedge(int x);
void setpoint(int x);

int main() {
  freopen("1.in", "r", stdin);
  qr(m); qr(n);
  for (int i = 1; i <= n; ++i) {
    for (int j = 1, k = m + i; j < k; ++j) {
      id[i][j][0] = ++t; id[i][j][1] = ++t;
      qr(MU[i][j]);
    }
  }
  s = ++t; ++t;
  setpoint(1);
  setedge(1);
  EK();
  setpoint(INF);
  setedge(1);
  EK();
  setpoint(INF);
  setedge(INF);
  EK();
  return 0;
}

void setpoint(int x) {
  for (int i = 1; i <= t; ++i) {
    delete hd[i];
    hd[i] = NULL;
  }
  for (int i = 1; i <= m; ++i) {
    cont(s, id[1][i][0], 1, 0);
  }
  for (int i = 1; i <= n; ++i) {
    for (int j = 1, k = i + m - 1; j <= k; ++j) {
      cont(id[i][j][0], id[i][j][1], x, MU[i][j]);
    }
  }
}

void setedge(int x) {
  for (int i = 1; i < n; ++i) {
    int di = i + 1;
    for (int j = 1, k = i + m - 1; j <= k; ++j) {
      cont(id[i][j][1], id[di][j][0], x, 0);
      cont(id[i][j][1], id[di][j + 1][0], x, 0);
    }
  }
  for (int j = 1, k = m + n - 1; j <= k; ++j) cont(id[n][j][1], t, INF, 0);
}

void EK() {
  ans = 0;
  while (spfa()) argu();
  qw(ans, '\n', true);
}

bool spfa() {
  memset(canag, 0, sizeof canag);
  for (int i = 1; i <= t; ++i) dist[i] = -INF;
  dist[s] = 0; Q.push(s); canag[s] = INF;
  while (!Q.empty()) {
    int u = Q.front(); Q.pop(); inq[u] = false;
    for (auto e = hd[u]; e; e = e->nxt) if (e->flow > 0) {
      int v = e->v;
      if (dist[v] < (dist[u] + e->fee)) {
        dist[v] = dist[u] + e->fee;
        if (!inq[v]) Q.push(v);
        inq[v] = true;
        canag[v] = std::min(canag[u], e->flow);
        pre[v] = e;
      }
    }
  }
  return dist[t] != -INF;
}

void argu() {
  ans += canag[t] * dist[t];
  for (auto e = pre[t]; e; e = pre[e->u]) {
    e->flow -= canag[t]; e->bk->flow += canag[t];
  }
}