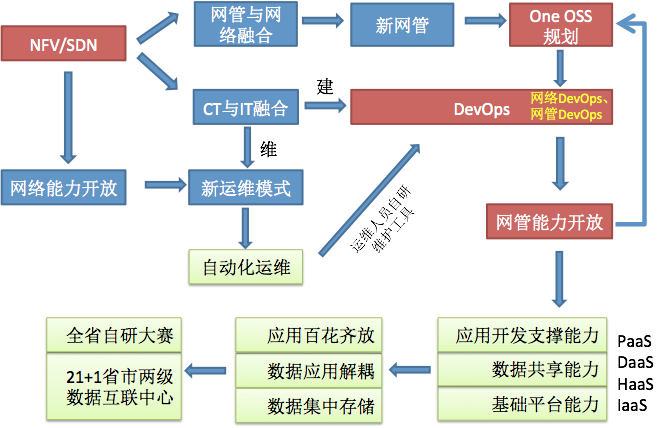
NFV/SDN驱动OSS转型的更多相关文章

  1. 麦格理银行借助DataStax Enterprise (DSE) 驱动数字化转型

    在本文中,我们将介绍DataStax Enterprise是如何助力澳大利亚最大的投资银行麦格理银行的数字银行,实现了实时分析和自然语言搜索等多项功能,并为用户提供了个性化的用户体验. "D ...

  2. OpenStack环境中的NFV实践

    原文链接:http://www.99cloud.net/html/2016/jiuzhouyuanchuang_1103/250.html 在开始实践之前我们首先需要了解一些NFV概念和术语. NFV ...

  3. Android 开发之 ---- 底层驱动开发(一) 【转】

    转自:http://blog.csdn.net/jmq_0000/article/details/7372783 版权声明:本文为博主原创文章,未经博主允许不得转载. 驱动概述 说到 Android ...

  4. Android 开发之 ---- 底层驱动开发(一)

    驱动概述 说到 android 驱动是离不开 Linux 驱动的.Android 内核采用的是 Linux2.6 内核 (最近Linux 3.3 已经包含了一些 Android 代码).但 Andro ...

  5. CIO在数字化转型中如何正确定位？

    在数字化转型的大潮下,CIO和传统企业应如何抓住数字生态系统中的机遇?CIO该如何面对领导力.资金.技术和人才的挑战? Gartner研究总监陈勇表示:IT部门在企业中应转变成为一个引领创新的部门,C ...

  6. alsa和oss声音系统比较

    OSS(Open Sound System) OSS的含义为,Open Sound System,是unix平台上一个统一的音频接口.以前,每个Unix厂商都会提供一个自己专有的API,用来处理音频. ...

  7. Linux音频驱动-ALSA概述

    概述 ALSA(Advanced Linux Sound Architecture)是linux上主流的音频结构,在没有出现ALSA架构之前,一直使用的是OSS(Open Sound System)音 ...

  8. 基于TMF SID的高可扩展性数据模型

    基于TMF SID的高可扩展性数据模型 前言 此文根据TMF SID规范撰写,欢迎大家提出建议和意见. TMF文档版权信息 Copyright © TeleManagement Forum 2013. ...

  9. 思科安全：加密流量威胁检测、加密流量威胁和恶意软件检测、识别无线干扰或威胁、Talos 情报源可加强对已知和新型威胁的防御、分布式安全异常检测

    思科DNA竞品比较工具 您的网络能够驱动数字化转型吗? 根据IDC调查,45%的受调研公司计划在未来两年内做好网络数字化的准备.查看数字化网络带来的结果和商业价值. 下载报告 思科 HPE 华为 Ar ...

随机推荐

  1. BZOJ囤题计划

    决定做一些题,学习jry,开坑(其实是填坑) 大概会刷的很慢,大家别鄙视我..欢迎鄙视 果然慢出翔了,还是填完吧.. 现在做了: 11 [2338][HNOI2011]数矩形 枚举对角线暴力水过,所有 ...

  2. 002 python语法入门

    一:基本数据类型知识点 1.基本数据类型 Number 数字 String 字符串 Bool 布尔 List 列表 Tuple 元组 Set 集合 Dictionary字典 2.分类 )标准的pyth ...

  3. javacript 实现两个数组的差集

    <script type="text/javascript">      var array1 = [1,2,3,4,5,6,7,8,9];      var arra ...

  4. OpenCV 基础笔记

    本文大部分内容来源于入门者的Python快速教程 - 番外篇之Python-OpenCV 本篇将介绍和深度学习数据处理阶段最相关的基础使用,并完成4个有趣实用的小例子: 延时摄影小程序 视频中截屏采样 ...

  5. Bazel

    Using Bazel on Windows Google软件构建工具Bazel FAQ

  6. TCP可靠传输及流量控制实现原理

    一.为什么TCP是可靠传输? 1. 停止等待协议 通过确认与超时重传机制实现可靠传输 在发送完一个分组后,必须暂时保留已发送的分组的副本. 分组和确认分组都必须进行编号. 超时计时器的重传时间应当比数 ...

  7. CSUOJ 1162 Balls in the Boxes 快速幂

    Description Mr. Mindless has many balls and many boxes,he wants to put all the balls into some of th ...

  8. spring 事务配置

    事务配置文档xml <!-- from the file 'context.xml' --> <?xml version="1.0" encoding=" ...

  9. iOS 11开发教程（二）编写第一个iOS 11应用

    iOS 11开发教程(二)编写第一个iOS 11应用 编写第一个iOS 11应用 本节将以一个iOS 11应用程序为例,为开发者讲解如何使用Xcode 9.0去创建项目,以及iOS模拟器的一些功能.编 ...

  10. ELK收集openstack日志

    1.安装jdk 每个openstack服务器需要安装jdk,我安装的版本jdk-7u71-linux-x64.rpm 2.安装.配置Elastic Search install https://dow ...