Leetcode 1262. 可被三整除的最大和

题目：给你一个整数数组 nums，请你找出并返回能被三整除的元素最大和。

　　示例 1：

　　输入：nums = [3,6,5,1,8]
　　输出：18
　　解释：选出数字 3, 6, 1 和 8，它们的和是 18（可被 3 整除的最大和）。

　　这道题是第163周竞赛的一道题目，难度中等，边学别人的解题方法，边记录吧！

　　

方案一、不妨设dp[i] 代表 选取的数字累加和 模3 = i 的数字和　　

　　假定nums[i] % 3 = 1 ，那么，和 前面选取的数字和模 3 = 2 的数相加，就可以模3为 0 ，表达起来就是 dp[0] = max(dp[0], nums[i] + dp[2])依次类推，只要不断更新 dp 数组即可，注意一点，更新的时候要保存上一个状态的值，避免后续更新的时候重复影响。

　　

 #include <iostream>
 #include <vector>
 #include <algorithm>
 using namespace std;

 int maxSumDivThree(vector<int>& nums) {
     int dp[] = { , ,  };
     int i;
     cout << "┌───────┬───────┬───────┐" << endl;
     for (i = ; i < nums.size(); i++)
     {
         //依次判断nums[i]
         int mod = nums[i] % ;
         int a = dp[( +  - mod) % ];//保留上一步的值，避免后续相加影响
         int b = dp[( +  - mod) % ];
         int c = dp[( +  - mod) % ];

         if (a||mod == ) dp[] = max(dp[], a + nums[i]);
         if (b||mod == ) dp[] = max(dp[], b + nums[i]);
         if (c||mod == ) dp[] = max(dp[], c + nums[i]);
         cout << "│\t" << dp[] << "\t│\t" << dp[] << "\t│\t" << dp[] << "\t│" << endl;
         if(i<nums.size()-)
             cout << "├───────┼───────┼───────┤" << endl;
         else
             cout << "└───────┴───────┴───────┘" << endl;
     }

     return dp[];
 }

 vector<int> vc;
 int main()
 {
     int n;
     cin >> n;
     vc.resize(n);
     int i;
     for (i = ; i < n; i++)
         cin>>vc[i];
     cout << endl;
     cout << "能被3整除的最大和为：" <<maxSumDivThree(vc) << endl;
     return ;
 }

理解：（当然这是看的别人的想法，作者https://leetcode-cn.com/u/igamegum/）

　　先看下运行结果吧，就用上边的实例进行解释：

　　

　　 1、a,b,c是干什么用的？

　　a，b，c应该是保留上一步的值，a、b、c的取值如下：

　　

　　每次均记录了上一步的dp中的值，下一步在计算dp[0]时，dp[0]会发生变化，此时，在计算dp[1]时，用到的dp[0]不再是原始的dp[0]，从而造成数据的不一致问题！

　　2、if(b || mod == 1)中，为什么还要判断b的值？

　　这里的b我理解的是，当它不为0的时候，不过mod值是不是1，我都需要去更新dp[1]，因为存在mod是2，需要考虑（2+2）%3=1的情况，同样，mod为0，需要考虑（1+0）%3=1的情况；这里我们去掉试一试，看下结果：

　　

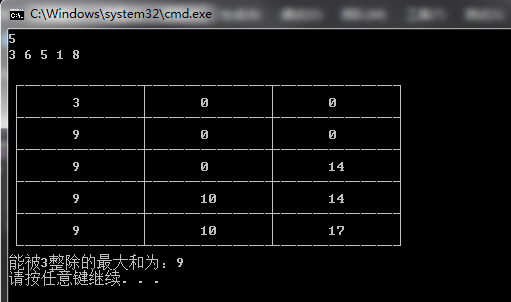
　　显然，当计算第4层时，数字1%3=1，此时，dp[0]只考虑了mod=0，所以dp[0]没有进行更新，但是数字1+dp[2]也可以构成模3余0的情况，并且和为15，显然比9大！！！

方案二、国外神代码，没解释，等待理解

 class Solution {
 public:
    int maxSumDivThree(vector<int>& A) {
         vector<int> dp = {, INT_MIN, INT_MIN};
         for (int a : A) {
             vector<int> dp2 = {, , };
             for (int i = ; i < ; ++i)
                 dp2[(i + a) % ] = max(dp[(i + a) % ], dp[i] + a);
             dp = dp2;
         }
         return dp[];
     }
 };

理解了之后回来更新~~~