[Algorithm] Graph

教学大纲

---

一、高教版《数据结构》

图的概念有点多，在此只讨论最基础的内容，所以选择比较薄的高教版《数据结构》。

1.4 非线性数据结构--图
1.4.1 图的基本概念
1.4.2 图形结构的物理存储方式
1.4.2.1 相邻矩阵
1.4.2.2 图的邻接表示
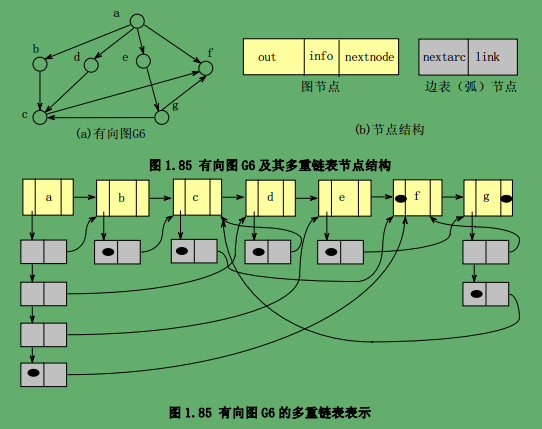
1.4.2.3 图的多重邻接表示
1.4.3 图形结构的遍历
1.4.4 无向连通图的最小生成树（minimum-cost spanning tree:MST）
1.4.5 有向图的最短路径
1.4.5.1 单源最短路径（single-source shortest paths）
1.4.5.2 每对顶点间最短路经（all-pairs shortest paths）
1.4.6 拓扑排序

二、网络资源

涉及到的内容：数据结构之图【还可以的大纲】

不错的教学视频：5 1 图的基本概念

三种表达

From: https://www.cs.usfca.edu/~galles/visualization/DFS.html

• • Logical Representation
  • Adjacency List Representation
  • Adjacency Matrix Representation

“普通”邻接表示

struct node{
　　bool mark; //访问标志
　　char letter; //顶点数据域
　　struct edge *out; //指向边表的指针
};
struct edge{
　　bool mark; //访问标志
　　int no; //顶点编号
　　struct edge *link; //指向边表的后继
};

多重邻接表示

表节点存储的不是顶点的序号，而是指向边（或者说弧）另一端相邻顶点的指针。

struct node{
　　bool mark; //访问标志
　　char letter; //顶点数据域
　　struct node *nextnode; //指向图顶点集合中下一个元素的指针
　　struct arc *out; //指向该顶点边表的指针
};
struct arc{
　　bool mark; //访问标志
　　struct node *link; //指向该弧（边）的另一端顶点的指针
　　struct arc *nextarc; // 指向与该顶点连接的其余弧（边）的指针
};

看上去特别像倒排表：[IR] Inverted Index & Boolean retrieval

图的遍历

一些概念

连通：如果从v到w存在一条（无向）路径，则称v和w是连通的

路径：v到w的路径是一系列的顶点的集合，其中任一对相邻的顶点间都有图中的边。路径的长度是路径中的边数（如果带权，则是所有边的权重和）。如果v和w之间的所有顶点都不同，则称简单路径（无回路）

回路：起点等于终点的路径

连通图：图中任意两顶点均连通

连通分量：无向图中的极大连通子图

强连通；有向图中顶点v和w之间存在双向路径（既有从v->w又有从w->v，可以不是同一条），则称v和w是强连通

弱连通：去掉方向后的v和w是连通的

强连通图：有向图中任意两顶点均强连通

强连通分量：有向图的极大强连通子图

遍历实现

不同的起点，会导致不同的遍历路径，也就生成了不同的“生成树”。

• • 深度优先(depth-first search:DFS)
  • 宽度优先(breadth-first search:BFS)

Depth First Search, DFS

Breadth First Search, BFS

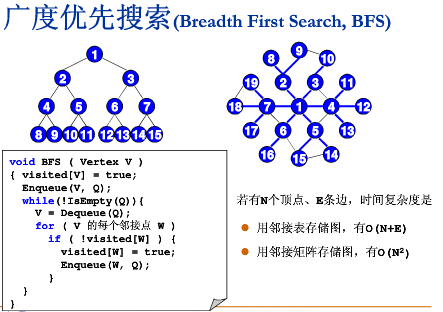
广度优先搜索六层，就是“六度空间” 问题。

图的优化问题

"无向连通图" 的最小生成树（minimum-cost spanning tree:MST）

既然从不同的顶点出发会有不同的生成树，而 n 个顶点的生成树有 n-1 条边，那么，当边带权的时候（网络），如何寻找一个（网络中）的最小生成树（即树中各边权值之和最小）？

以下内容具体参见：[Optimization] Greedy method

稠密图的贪心算法：Prim算法

从一个点一点一点向外扩张延伸，进入树内的点的dist都为0，往外延伸时是与树中任意一个结点距离最小

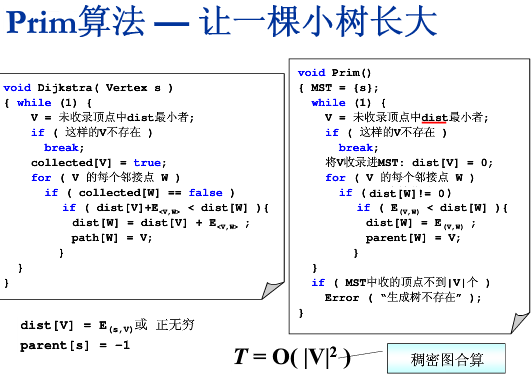
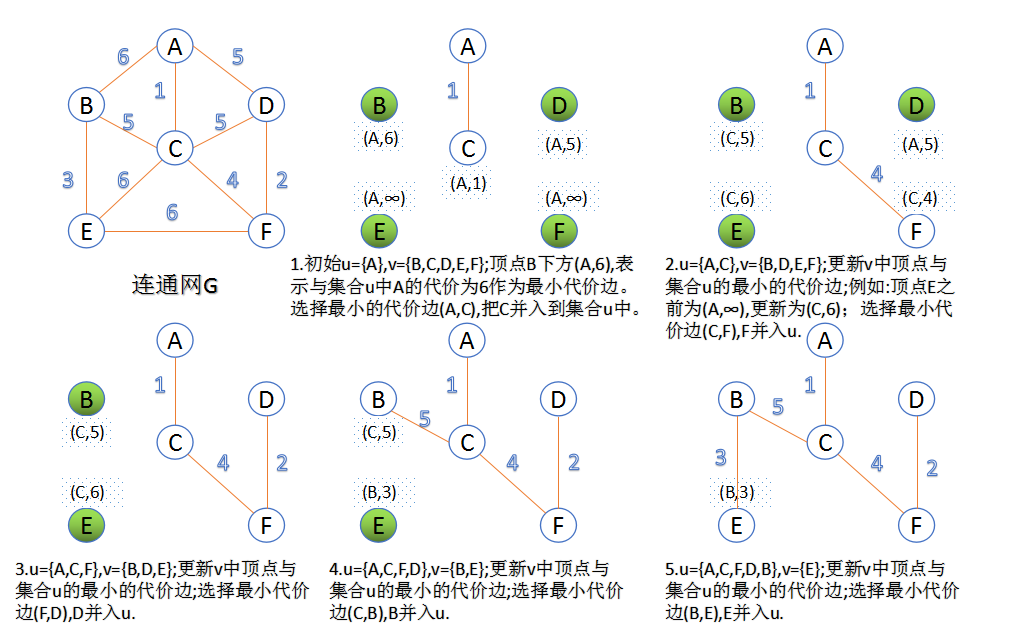
选择整个树周边的“最小的边”。

稀疏图的贪心算法：Kruskal算法

每次从剩余所有边中取最短的边，所选边不能构成回路

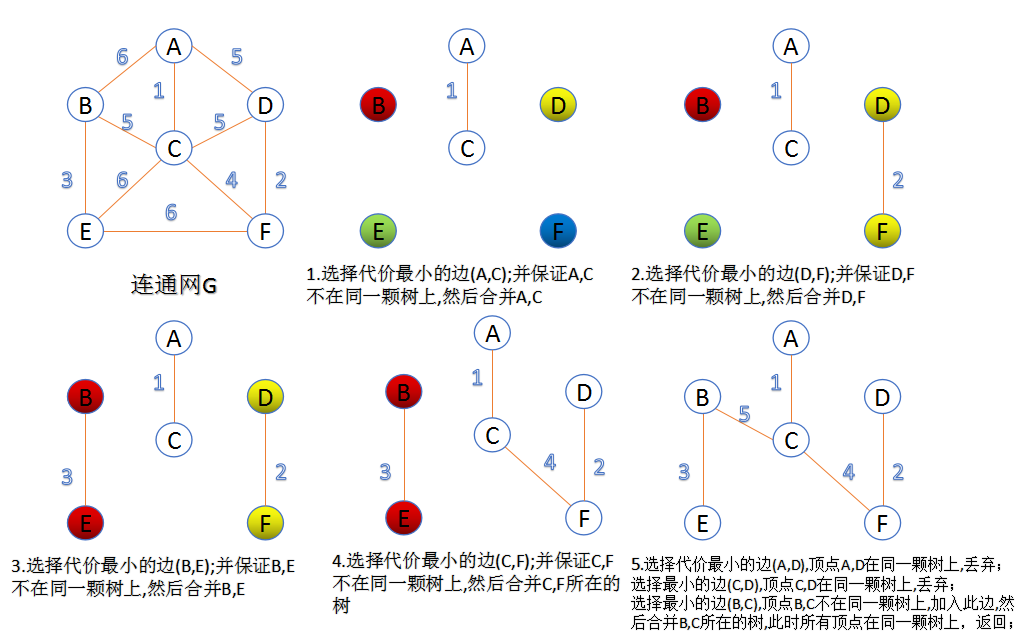
最小堆：查找最小的边

并查集：要连接的俩点不在同一棵树上。Goto: 超有爱的并查集

并查集的实现，int pre[1000]; 这个数组，记录了每个大侠的上级是谁。大侠们从1或者0开始编号（依据题意而定），pre[15]=3就表示15号大侠的上级是3号大侠。

如果一个人的上级就是他自己，那说明他就是掌门人了，查找到此为止。也有孤家寡人自成一派的，比如欧阳锋，那么他的上级就是他自己。每个人都只认自己的上级。比如胡青牛同学只知道自己的上级是杨左使。

张无忌是谁？不认识！要想知道自己的掌门是谁，只能一级级查上去。

路径压缩，每个人通过指针在某一处查询自己门派的头儿。如果join有门派合并事件，则只修改门派的头儿即可。

有向图的最短路径

单源最短路径（single-source shortest paths）Dijkstra算法 (基于贪心算法)

Dijkstra算法和 最小生成树Prim算法最小生成树算法非常类似，大家可以先熟悉下个算法。两个算法都是基于贪心算法。

虽然Dijkstra算法相对来说比Bellman-Ford 算法更快，但是不适用于有负权值边的图，贪心算法决定了它的目光短浅。

而Bellman-Ford 算法从全局考虑，可以检测到有负权值的回路。

Ref: Dijkstra算法(一)之 C语言详解

核心思路

与S集合中相邻的点中找到最小的(“边”＋相邻点的“值”)，然后更新俩集合即可。

如果edge存在负数，则会破坏以上这句话背后的原则。

时间复杂度：O(E+V*logV)

基本思想

指定起点s (即从顶点s开始计算)。

S：记录已求出最短路径的顶点 (以及相应的最短路径长度)；

U：记录还未求出最短路径的顶点 (以及该顶点到起点s的距离)；

初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶的路径是"起点s到该顶点的路径"。

然后，从U中找出路径最短的顶点，并将其加入到S中；

接着，更新U中的顶点和顶点对应的路径。

然后，再从U中找出路径最短的顶点，并将其加入到S中；

接着，更新U中的顶点和顶点对应的路径。 ... 重复该操作，直到遍历完所有顶点。

操作步骤

(1) 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为"起点s到该顶点的距离"[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。

(2) 从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k。

(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

(4) 重复步骤(2)和(3)，直到遍历完所有顶点。

每对顶点间最短路经（all-pairs shortest paths）Floyed算法 (基于动态规划)

Ref: Floyd 算法求多源最短路径

Floyd算法用来找出每对顶点之间的最短距离，它对图的要求是，

• • 既可以是无向图也可以是有向图，边权可以为负。
  • 但是不能存在负环 (可根据最小环的正负来判定)。

More details, please check : [Optimization] Dynamic programming

　　　　/* 其他内容，再补充 */

End.