本实验模拟公司场景 通过路由器实现不同vlan部门间通讯，拓扑图如下

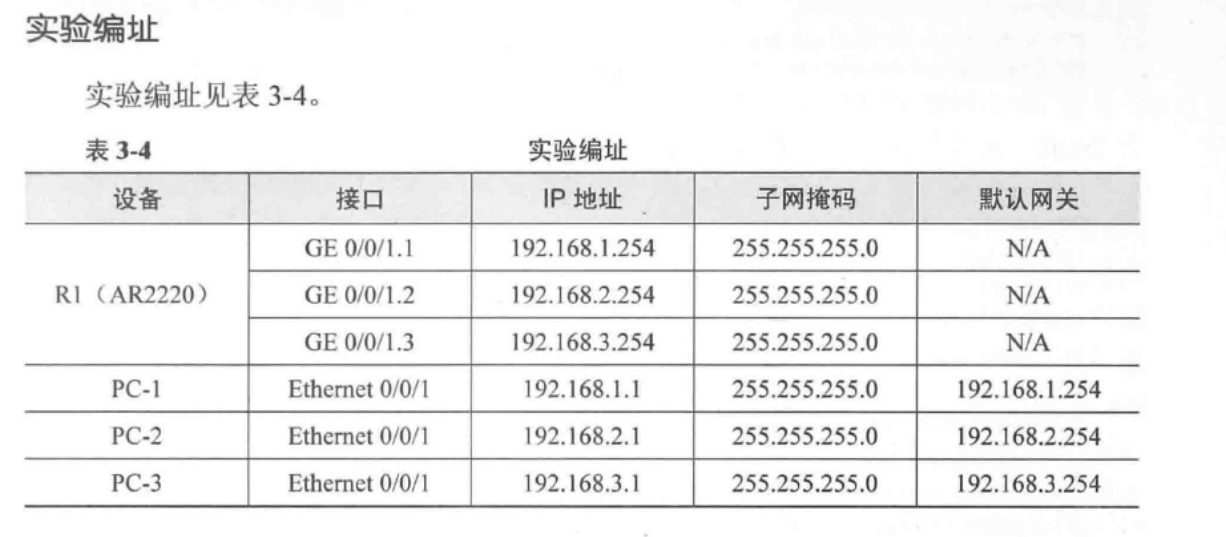
实验编址如上图所示。

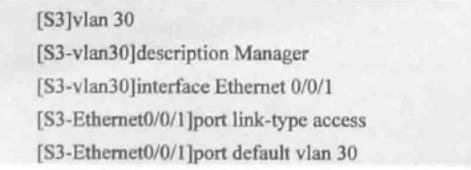
在两个交换机中添加vlan 并将与pc机连接的端口设置成access口 然后将端口划分进入各自的VLAN 中

然后将交换机与交换机，交换机与路由器连接的端口设置成Trunk口，因为要允许多个vlan通过 这里以S2的0/0/2端口举例

接着我们在路由器R1上创建子接口为各vlan 来实现vlan间路由 另外两个也一样

下一步 也是最关键的一步是   dot1q terminal vid 20 意思为 当路由器收到来自交换机发送的带有vlan 20 tag的报文后 将其tag剥掉并给报文添加上要转发的vlan的标签并转发出去

第二句命令开启子接口的arp广播功能 使得子接口可以转发报文。

现在我们使用display routing-table命令查看路由表就可以看到我们创建的子接口了 现在我们使用ping命令查看一下我们的结果

由此可见我们使用路由器实现不同vlan间路由成功了。

利用单臂路由实现vlan间路由的更多相关文章

  1. eNSP仿真软件之利用单臂路由实现VLAN间路由

    1. 实验原理 以太网中,通常会使用VLAN技术隔离二层广播域来减少广播的影响,并增强网络的安全性和可管理性.其缺点是同时也严格地隔离了不同VLAN之间的任何二层流量,使分属于不同VLAN的用户不能直 ...

  2. VLAN实验4（在eNSP上利用单臂路由实现VLAN间路由）

    原理概述: 以太网中,通常会使用VLAN技术隔离二层广播域来减少广播的影响*并增强 网络的安全性和可管理性.其缺点足同时也严格地隔离了不同VLAN之间的任何二层流量,使分属于不同VLAN的用户 不能直 ...

  3. VLAN实验4：利用单臂路由实现VLAN间路由

    单臂路由: 实验环境: 实验拓扑图: 实验编址: 实验步骤:1.创建VLAN并配置Access.Trunk接口. 我们在S2上创建VLAN10和VLAN20,并且吧链接PC1的E0/0/1和链接PC2 ...

  4. 在ensp上利用单臂路由实验VLAN间路由

    我们为什么要设置单臂路由? 因为我们要解决不同vlan,不同网络的PC机间的通信问题~ 那它为啥叫单臂路由嘞? 单臂路由的原理时通过一台路由器,使vlan间互通数据通过路由器进行三层转发,如果在路由器 ...

  5. eNSP——利用单臂路由实现VLAN间路由

    原理: 以太网中,通常会使用VLAN技术隔离二层广播域来减少广播的影响,并增强网络的安全性和可管理性.其缺点是同时也严格地隔离了不同VLAN之间的任何二层流量,使分属于不同VLAN的用户不能直接互相通 ...

  6. 利用单臂路由实现VLAN间路由（有1个疑问）

    配置PC机: PC1:IP 192.168.1.1 :掩码:255.255.255.0:网关:192.168.1.254  VLAN 10 PC2:IP 192.168.2.1 :掩码:255.255 ...

  7. 利用单臂路由实现VLAN间的路由

    实验4:利用单臂路由实现VLAN间的路由. 实验原理:  实验内容: 本实验模拟公司网络场景,路由器R1是公司的出口网关,员工PC通过接入层交换机(如S2和S3)接入公司网络,接入层交换机又通过汇聚交 ...

  8. 路由器基础配置之单臂路由实现vlan间通信

    我们将以上面的拓扑图开始进行配置,目的为设置单臂路由实现vlan间通信,设置4个vlan,pc0,1,2为vlan10 pc3,4,5为vlan20:pc6,7,8为vlan30:server0,1为 ...

  9. VLAN实验5（在ensp上利用三层交换机实现VLAN间路由）

    原理概述: VLAN将一个物理的LAN在逻辑上划分成多个广播域.VLAN内的主机间可以直接通信,而VLAN间不能直接互通. 在现实网络中,经常会遇到需耍跨VLAN相互访问的情况,工程师通常会选择一些方 ...

随机推荐

  1. 100: cf 878C set+并查集+链表

    $des$Berland要举行 $n$ 次锦标赛,第一次只有一个人,之后每一次会新加入一个人.锦标赛中有 $k$ 种运动项目,每个人在这 $k$ 种项目上都有一个能力值,每次会选择任意两个还未被淘汰的 ...

  2. NOIP2015 D1 解题报告

    T1 神奇的幻方 题目描述 幻方是一种很神奇的N*N矩阵:它由数字1,2,3,……,N*N构成,且每行.每列及两条对角线上的数字之和都相同. 当N为奇数时,我们可以通过以下方法构建一个幻方: 首先将1 ...

  3. 【概率论】6-4:分布连续性修正(The Correction for Continuity)

    title: [概率论]6-4:分布连续性修正(The Correction for Continuity) categories: - Mathematic - Probability keywor ...

  4. 2019 ACM-ICPC 西安全国邀请赛 E-Tree 树链剖分+线段树

    题意 给一颗带点权的树,三种操作 \(1~s~t\) 修改从1到s的路径上的所有点,\(a[i]=a[i]|t\) \(2~s~t\) 修改从1到s的路径上的所有点,\(a[i]=a[i]\& ...

  5. Magma中ECC的点乘实例

    a:=-3;b:= 41058363725152142129326129780047268409114441015993725554835256314039467401291;E:= Elliptic ...

  6. 《挑战30天C++入门极限》入门教程:C++中的const限定修饰符

        入门教程:C++中的const限定修饰符 const修饰符可以把对象转变成常数对象,什么意思呢? 意思就是说利用const进行修饰的变量的值在程序的任意位置将不能再被修改,就如同常数一样使用! ...

  7. Resolving EACCES permissions errors when installing packages globally(npm 遇到 write access的问题)

    If you see an EACCES error when you try to install a package globally, you can either: Reinstall npm ...

  8. UOJ#339. 【清华集训2017】小 Y 和二叉树 贪心

    原文链接 www.cnblogs.com/zhouzhendong/p/UOJ339.html 前言 好久没更博客了,前来更一发. 题解 首先,我们考虑一个子问题:给定根,求出最小中序遍历. 如果根节 ...

  9. Bootstrap selectpicker 下拉框多选获取选中value和多选获取文本值

    1.页面代码: 页面引入: bootstrap-select.min.css和 bootstrap-select.min.js. defaults-zh_CN.min.js文件,并初始化下拉选项框. ...

  10. 6、vueJs基础知识06

    vue动画 transition 之前1.0版本是以 属性的形式展示的 <p transition="fade"></p> .fade-transition ...