ML-学习提纲1

http://www.sohu.com/a/130379077_468714

本文用一系列「思维导图」由浅入深的总结了「统计学」领域的基础知识，是对之前系列文章做的一次完整的梳理，也是我至今为止所有与统计有关的学习笔记。众所周知，「统计学」是深入理解「机器学习|数据挖掘」的重要基础学科。正所谓磨刀不误砍柴工，对于数理基础薄弱的人，强化一下理论的学习是大有裨益的。普通人难以做到“一次学习”，经典知识总是在一次次回顾后才能有更深入的理解。这也是我选择「思维导图」作为学习工具的原因，发散性思考的模式能帮助迅速回忆起相关的知识。近一个月我对之前陆陆续续学习的统计知识进行了系统性的复习、知识点补充以及思维导图笔记的完善，在这里把完整的笔记和大家分享。本文图片很多，请在wifi下阅读哦。

思维导图说明

• 默认阅读顺序：从右→左，顺时针方向。

• 核心重点用「红色星星」标出，需要重点理解，一般是后续学习的基石；「绿色星星」则为需要进一步巩固的内容；「蓝色星星」为高级部分，可以暂时不深入；「红色旗子」表示并列层级，「绿色旗子」为下一层级；「黄色星星」表示需要注意的内容点。

• 「箭头线」标出了知识之间的联系。

• 文末附上了分章节整理的链接及百度云盘文件分享，可以根据需要阅读。

• 笔记只是我学习过程的知识整理，本来是我自己复习时辅以参考的， 难免有缺陷及错误，希望大家能积极帮我批评指正哦。

>>>>

导图概览

>>>>

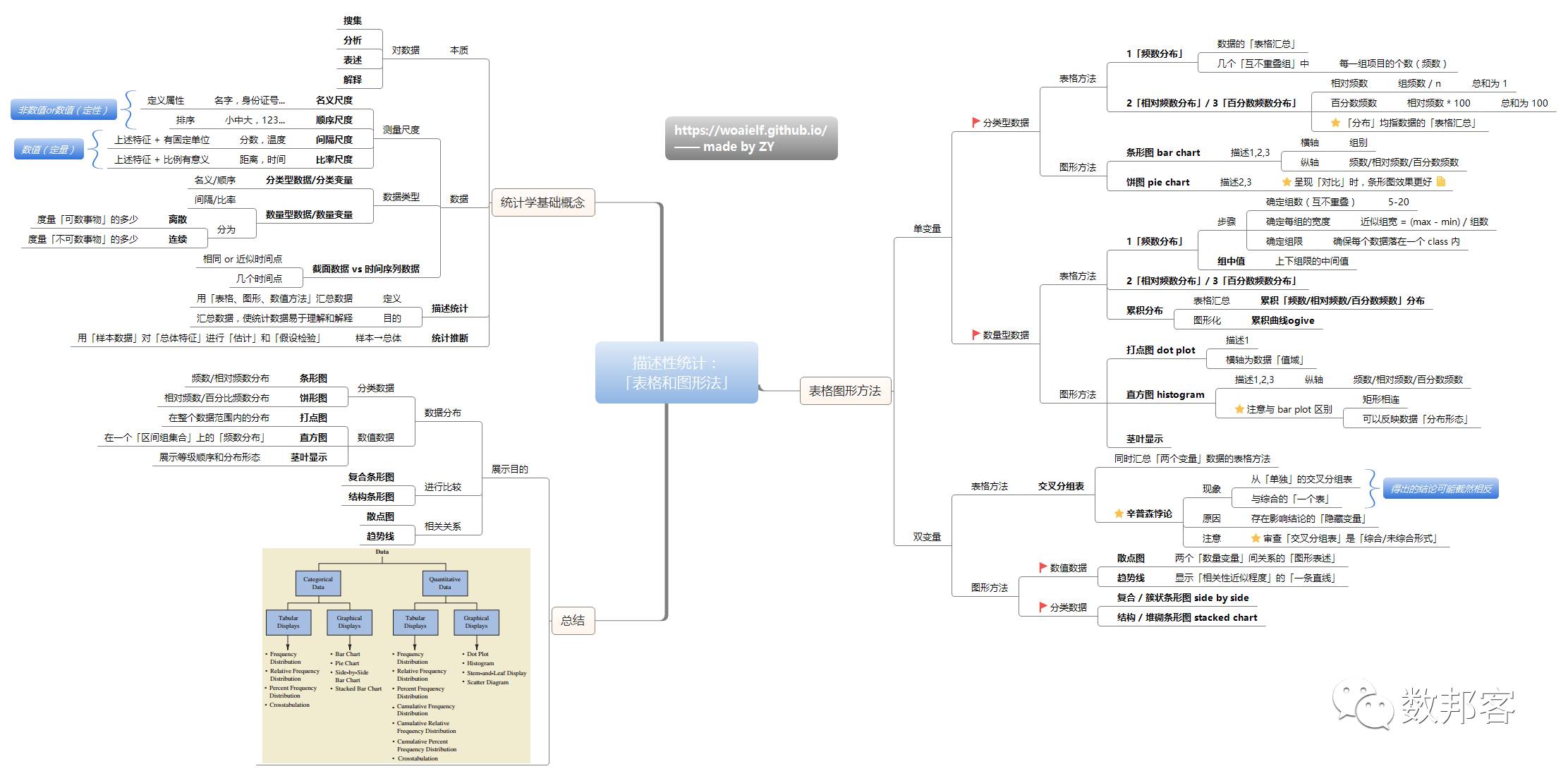
描述性统计：表格和图形法

>>>>

描述性统计：数值方法

>>>>

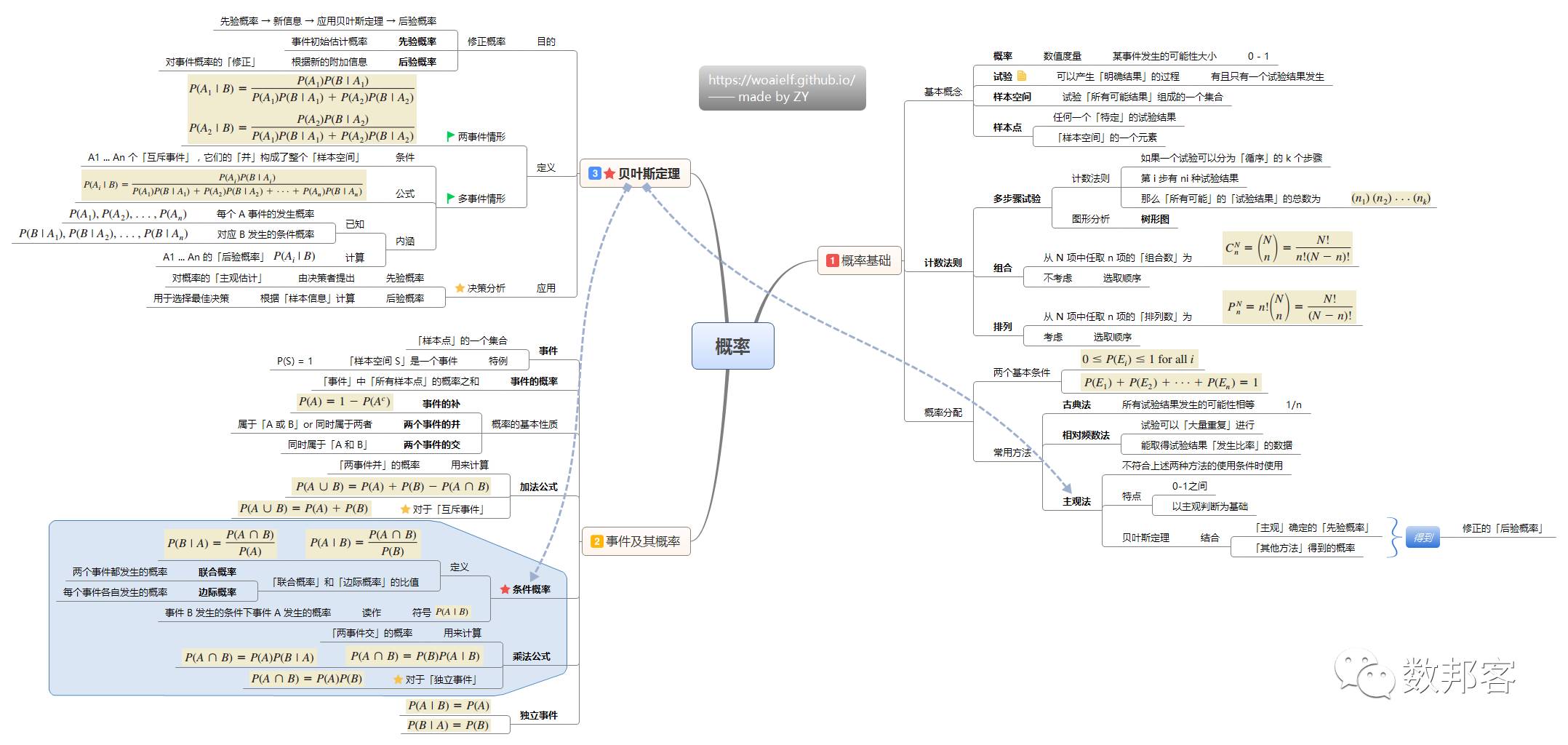
概率

>>>>

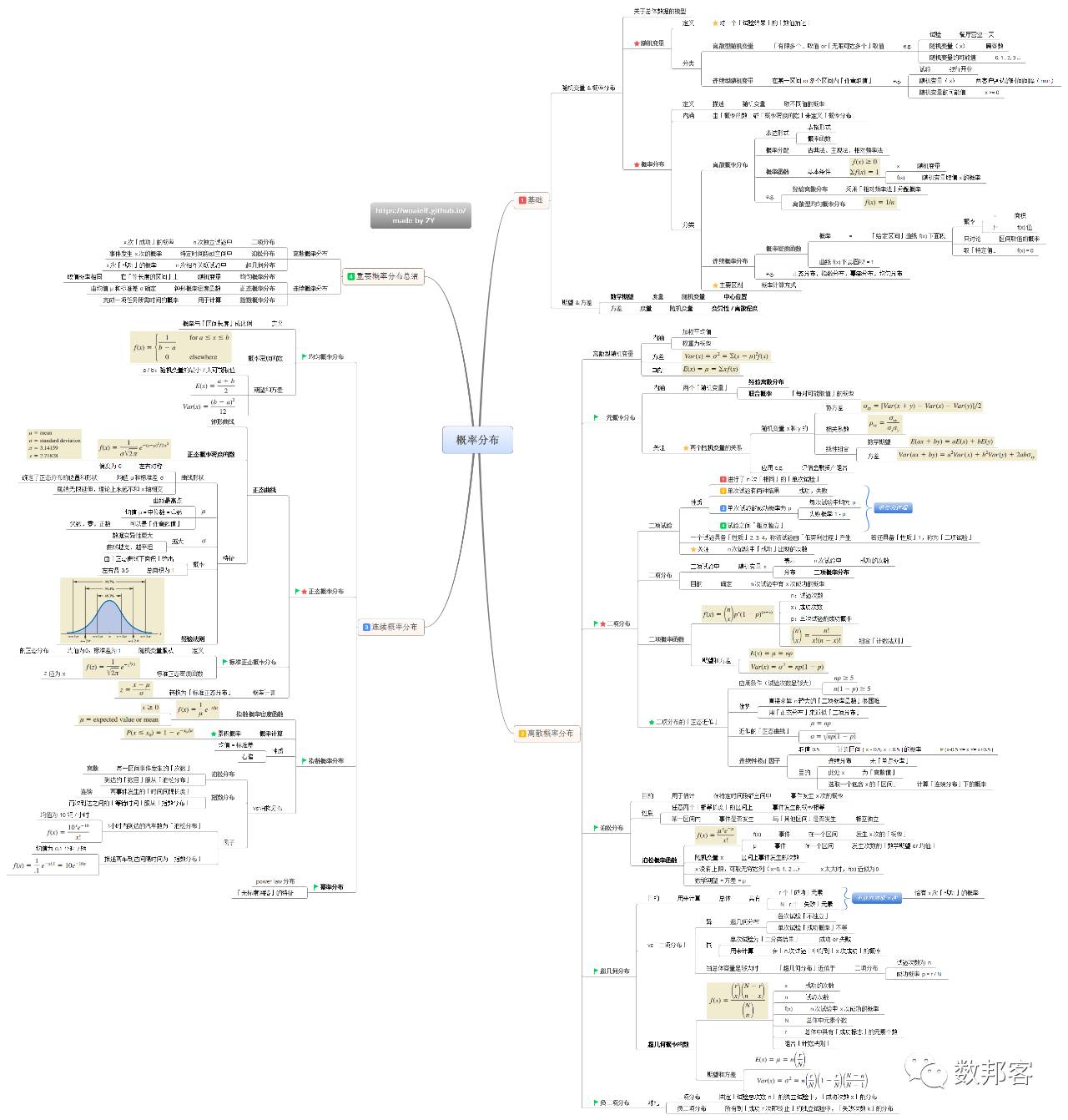
概率&概率分布

>>>>

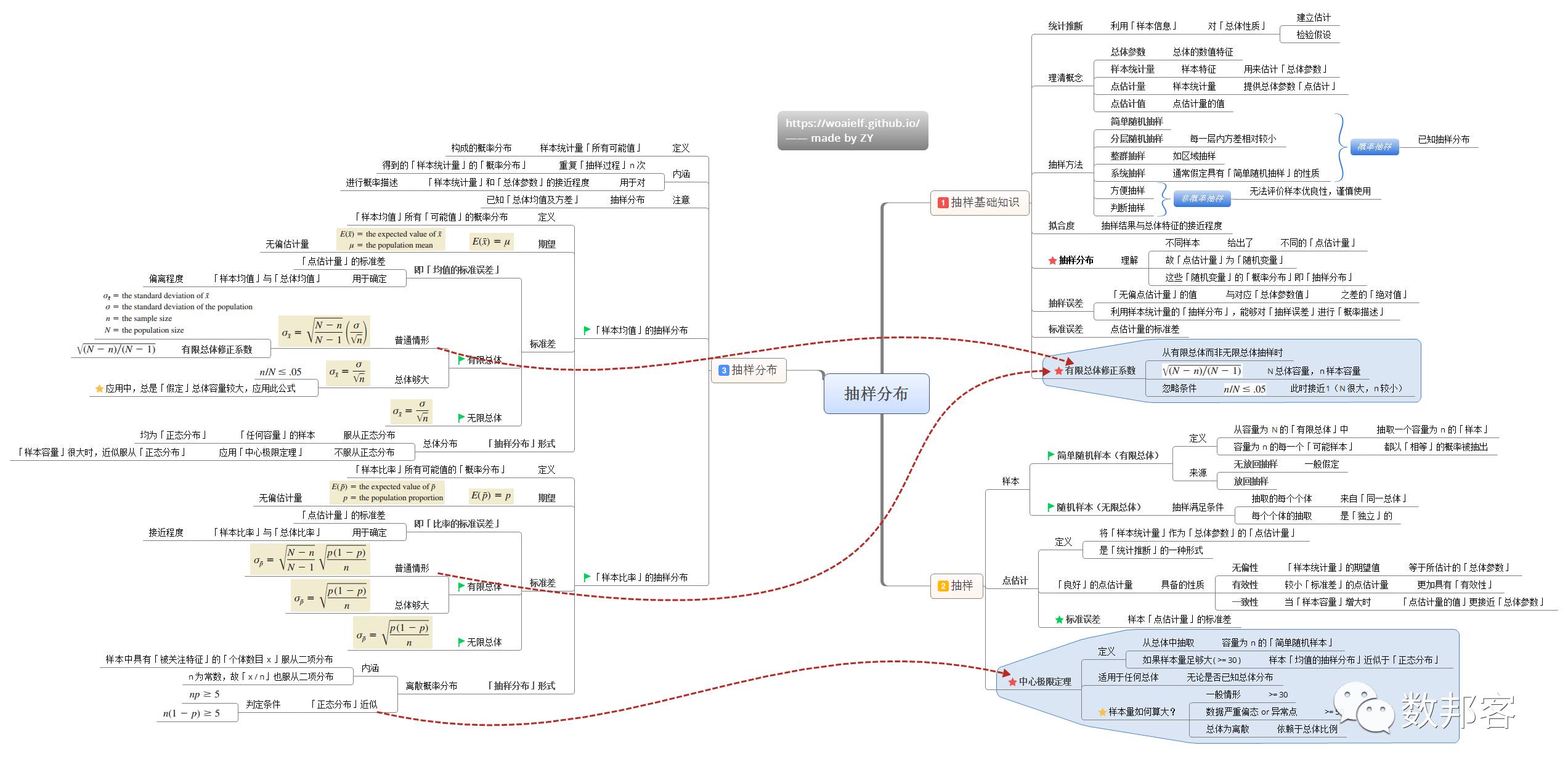
抽样分布

>>>>

区间估计

>>>>

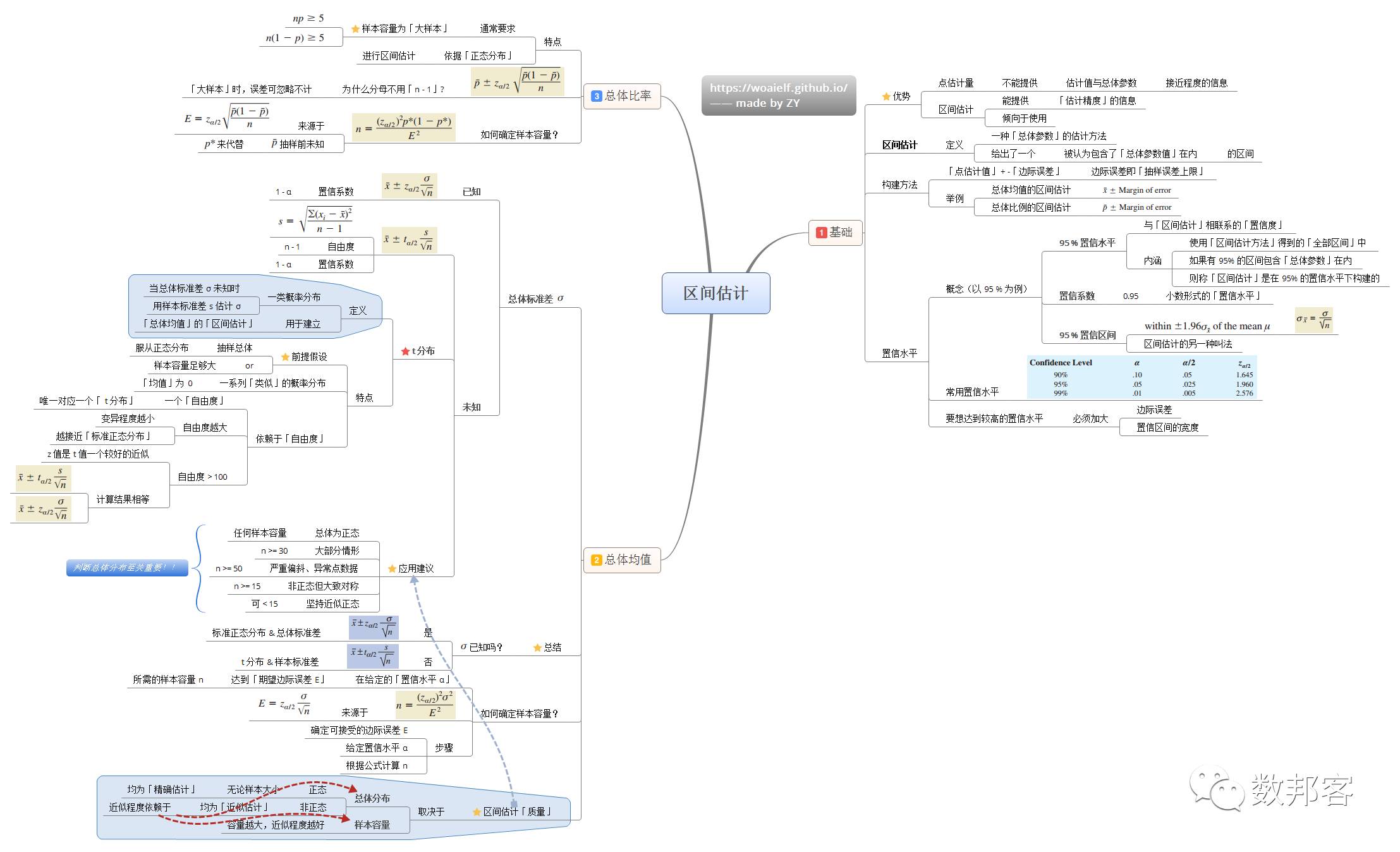
假设检验

>>>>

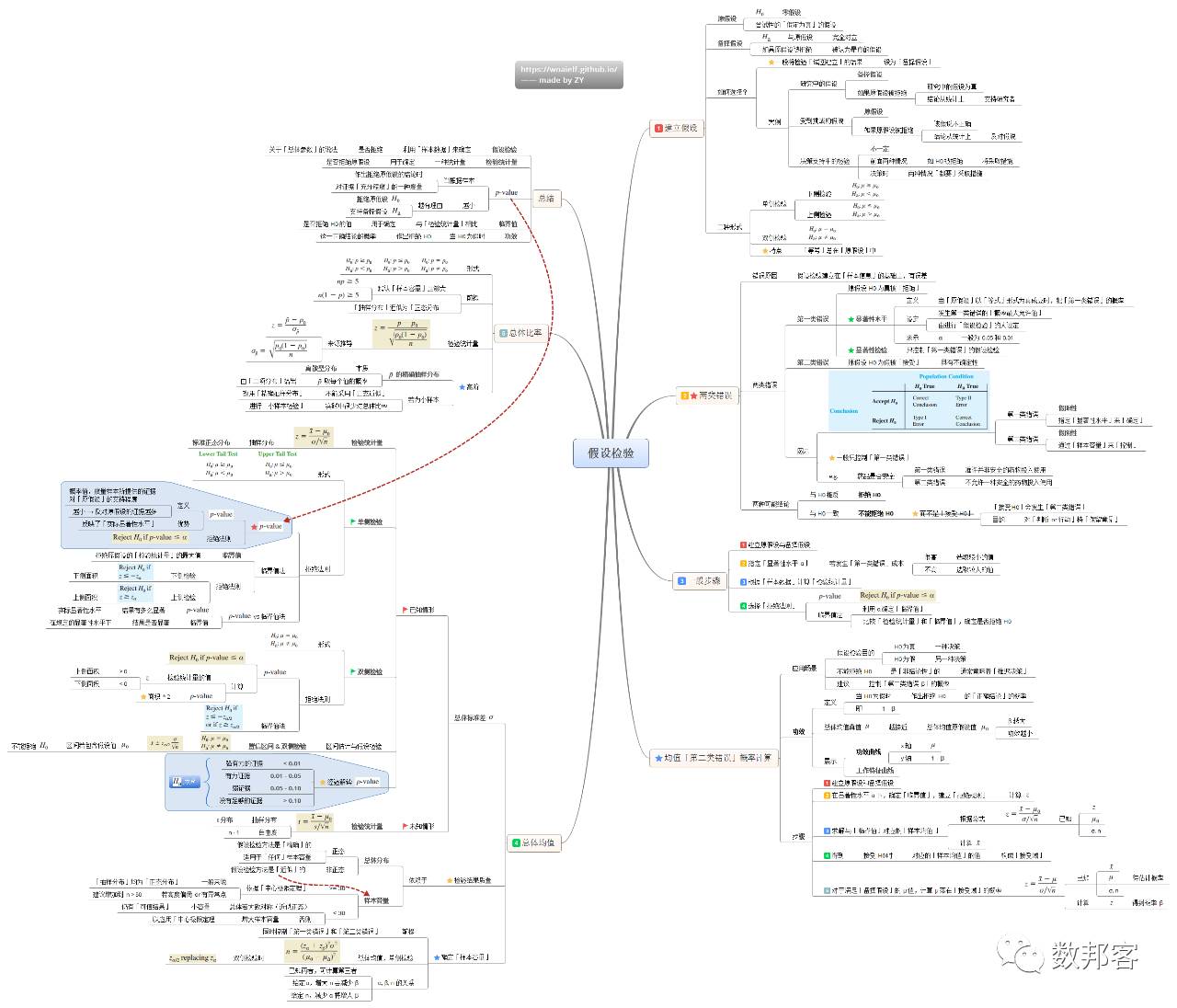
两总体均值之差和比例之差的推断

>>>>

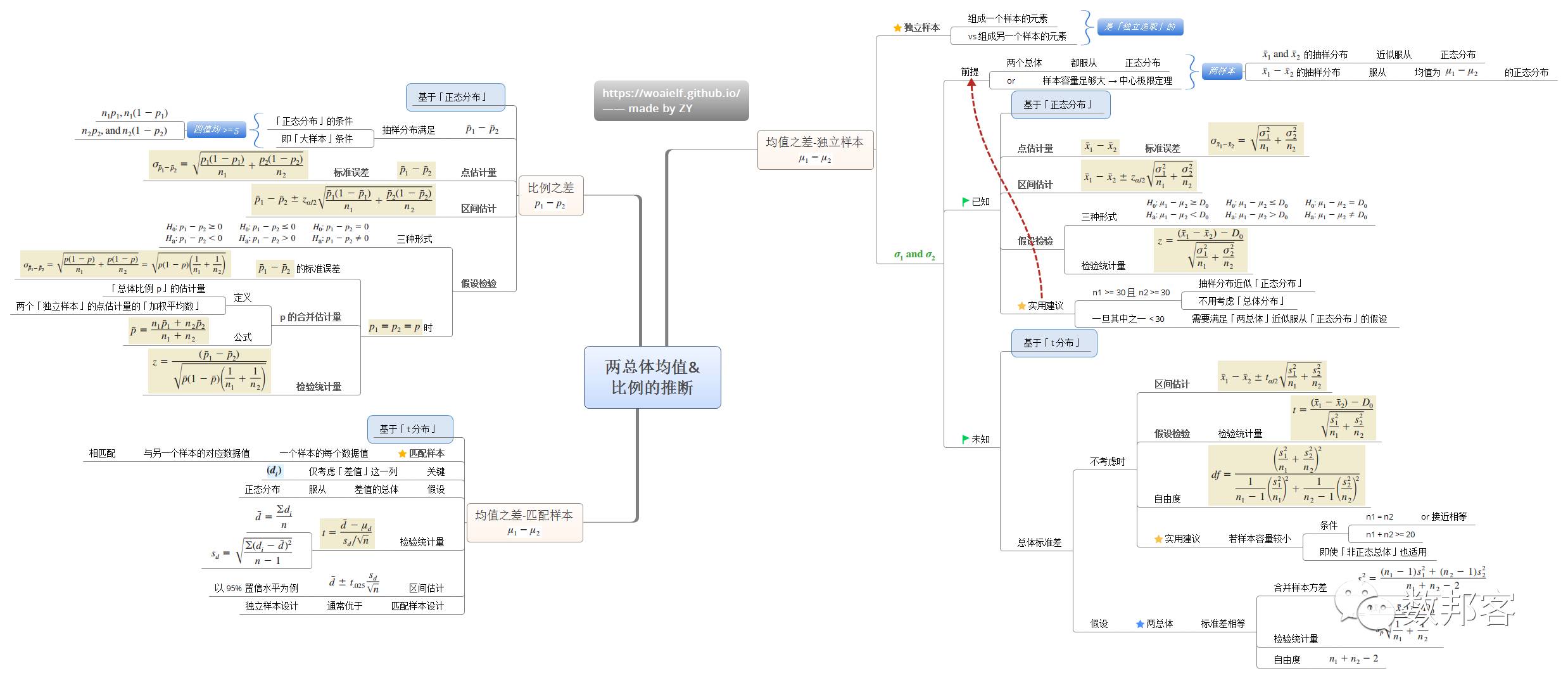
总体方差的统计推断

>>>>

多个比率的比较&独立性检验&拟合优度检验

>>>>

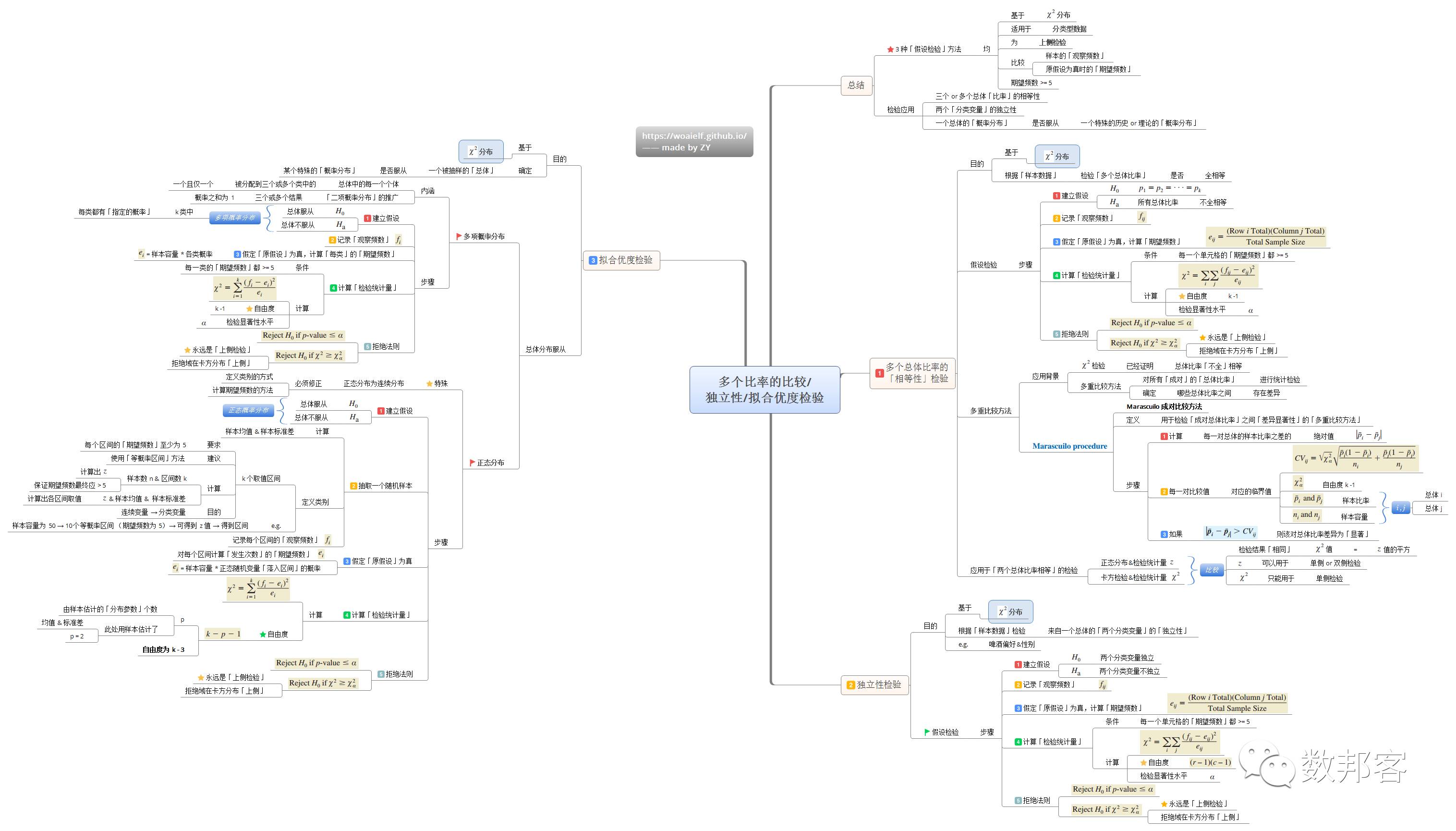
实验设计&方差分析

>>>>

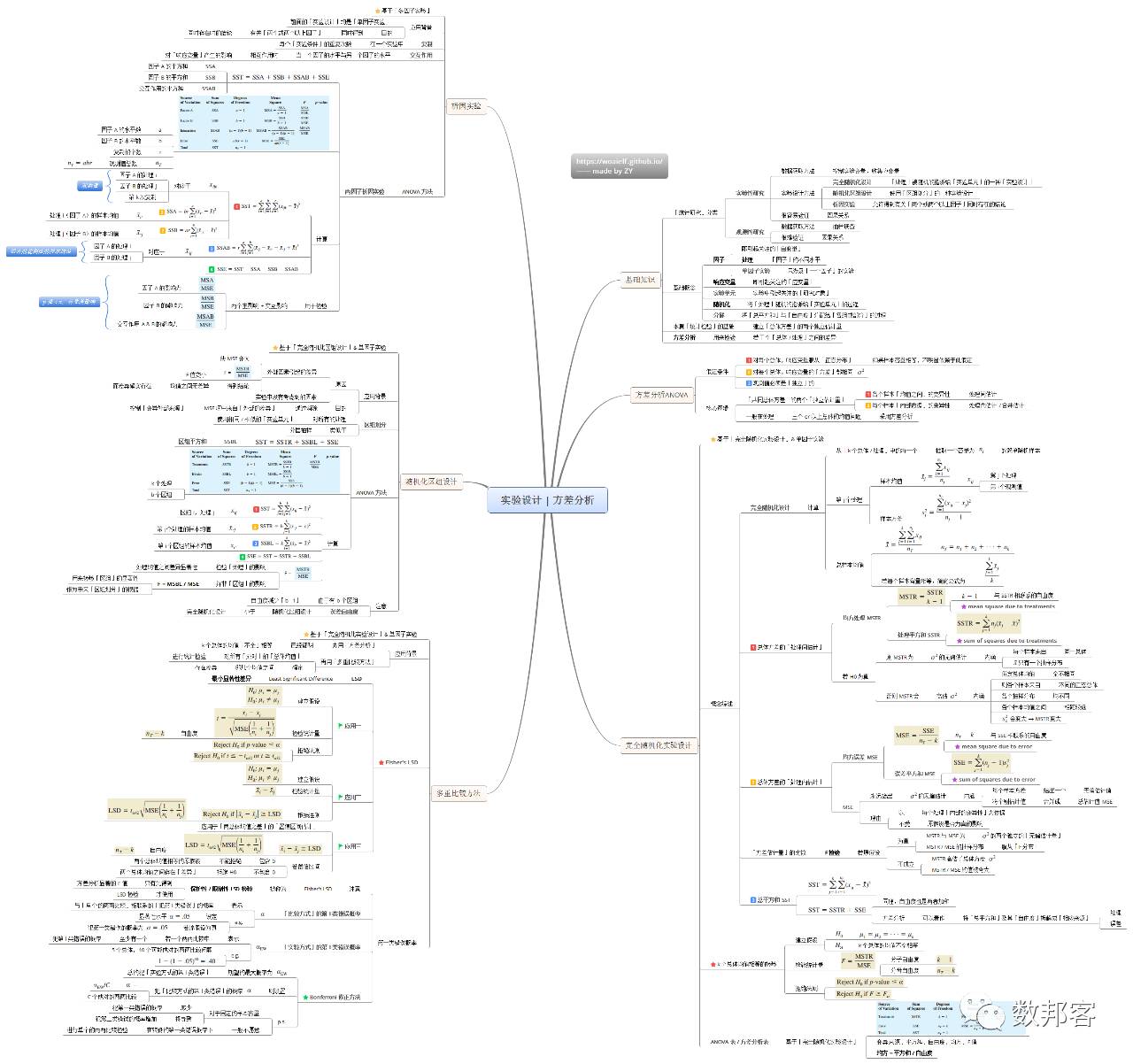
简单线性回归

>>>>

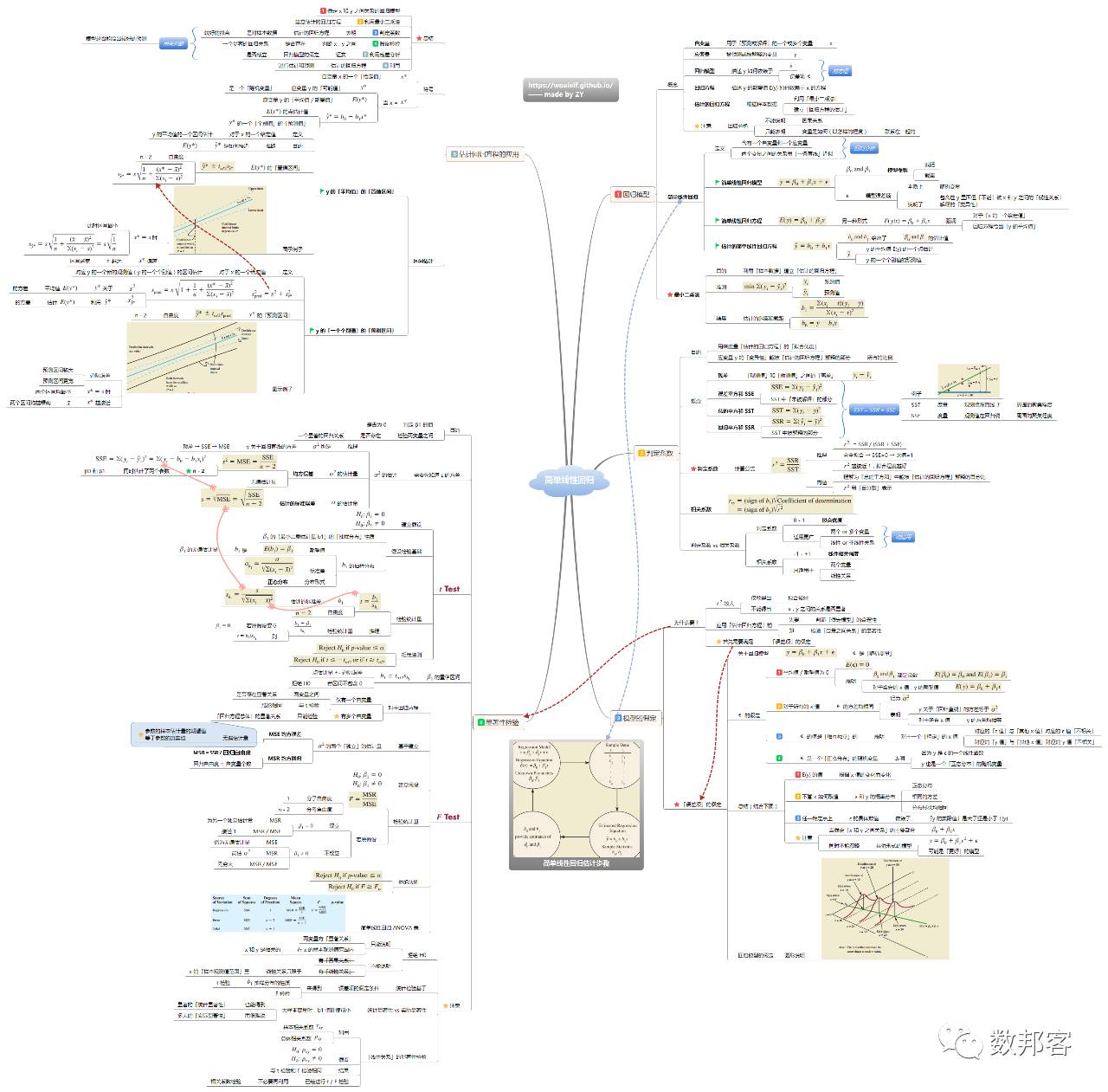
残差分析

>>>>

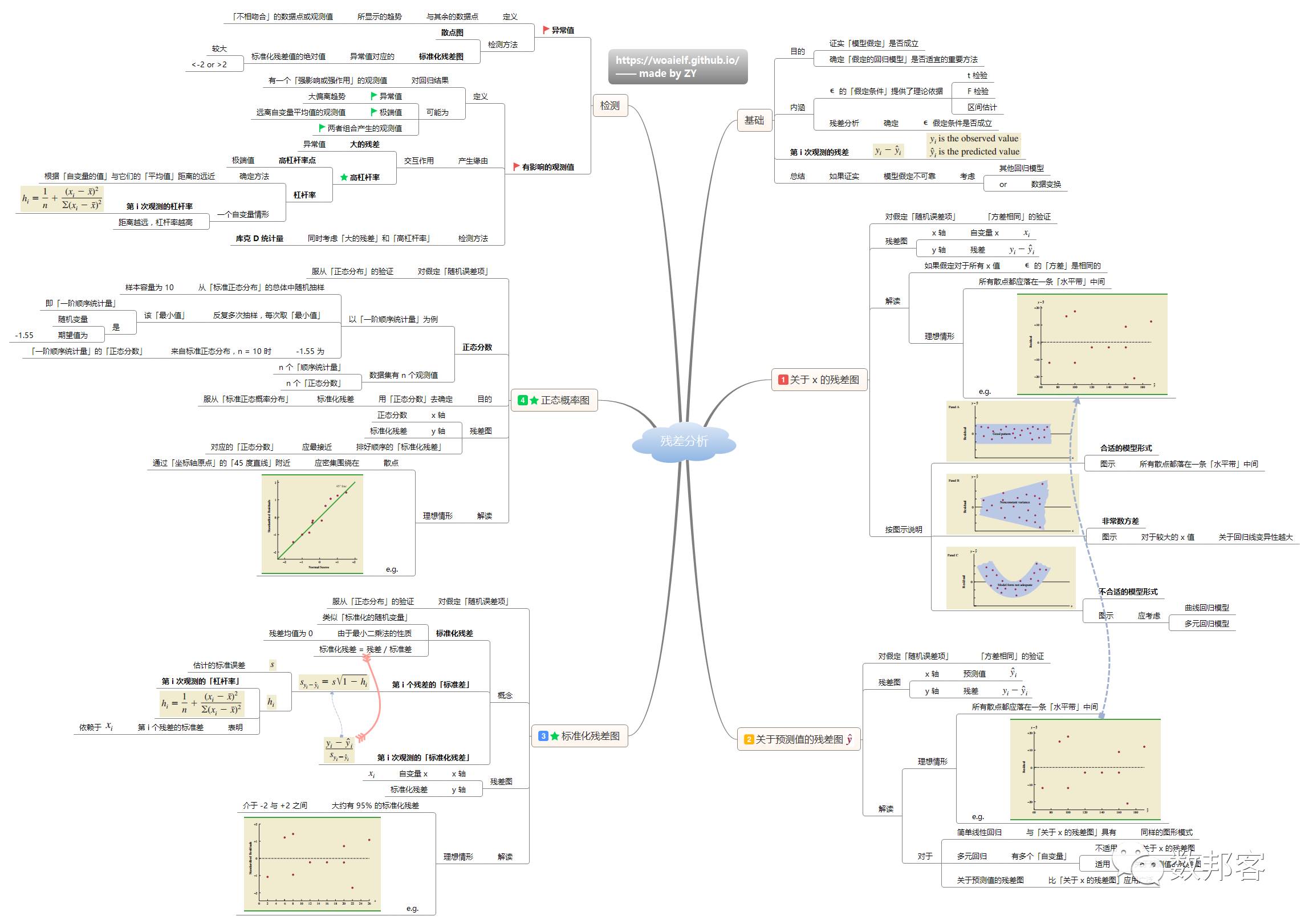
多元回归

>>>>

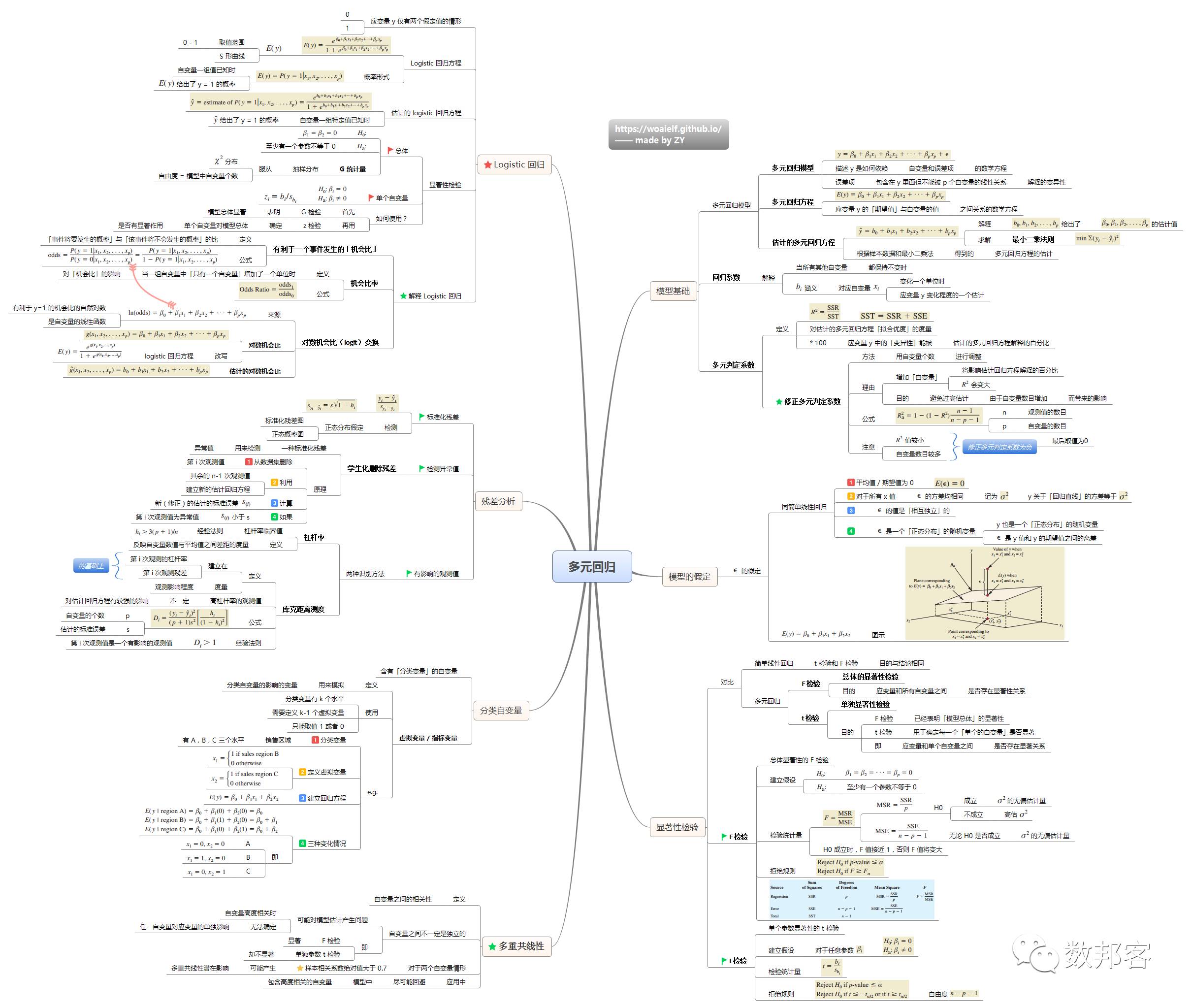
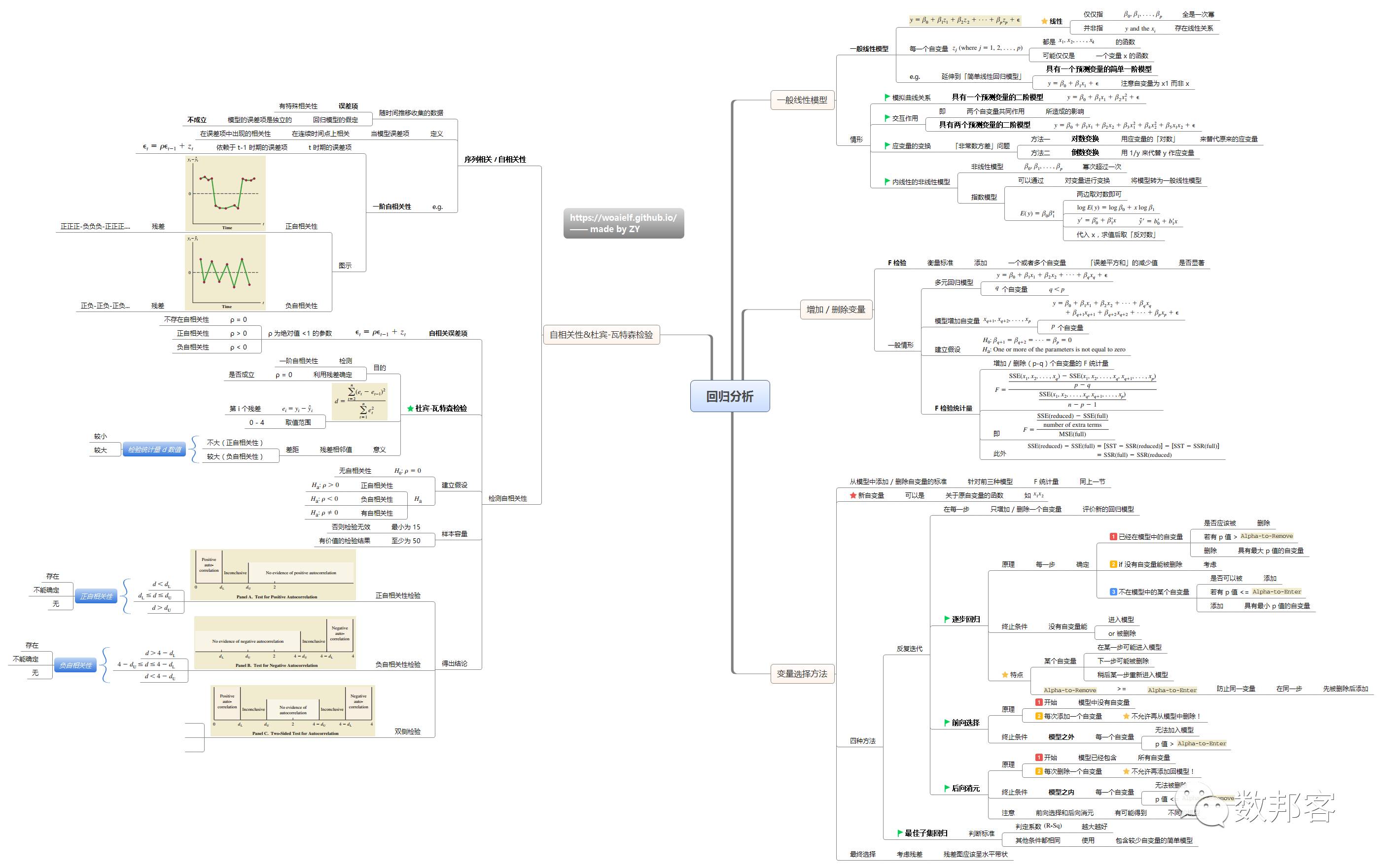
回归分析

>>>>

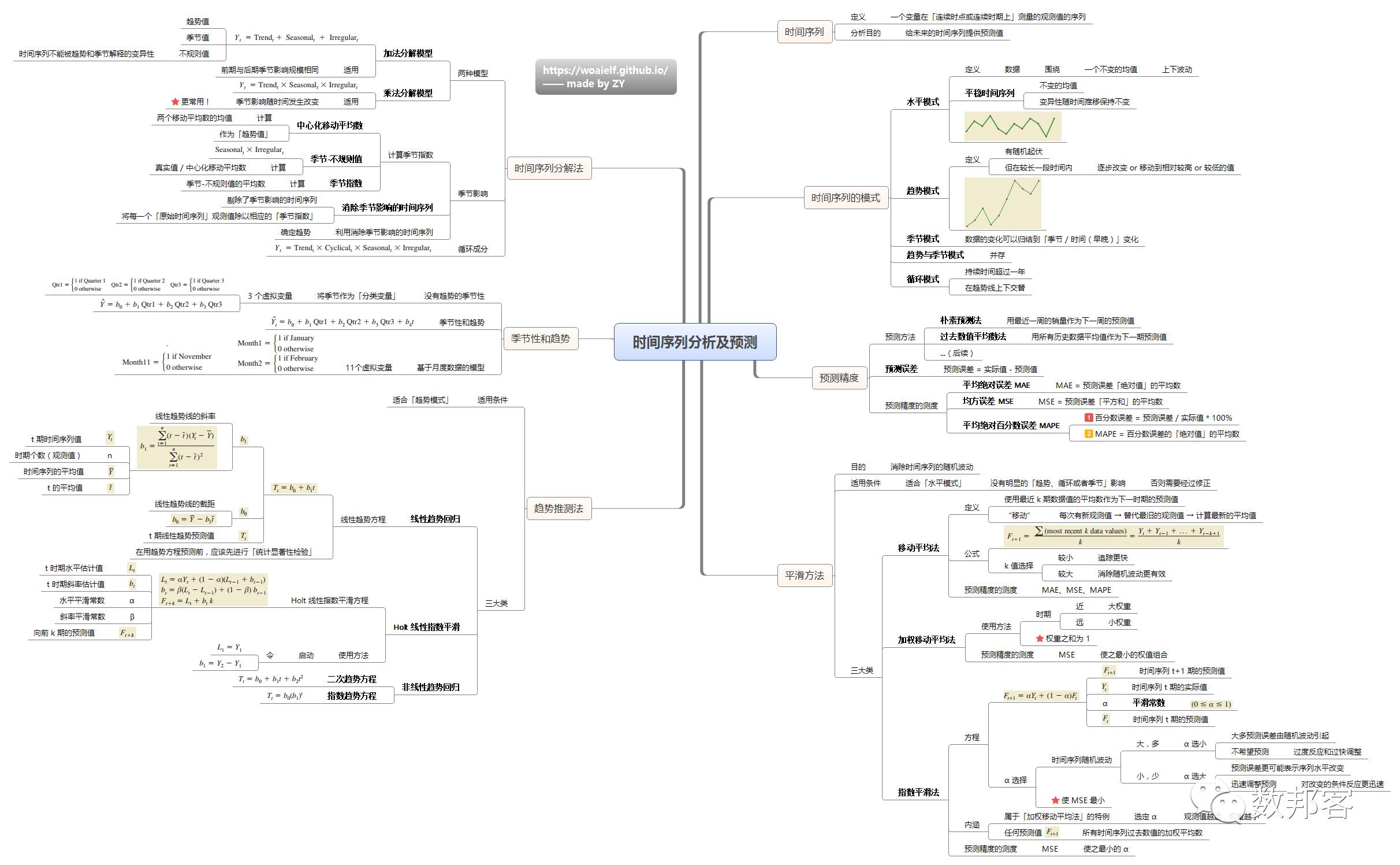
时间序列及预测

>>>>

非参数方法

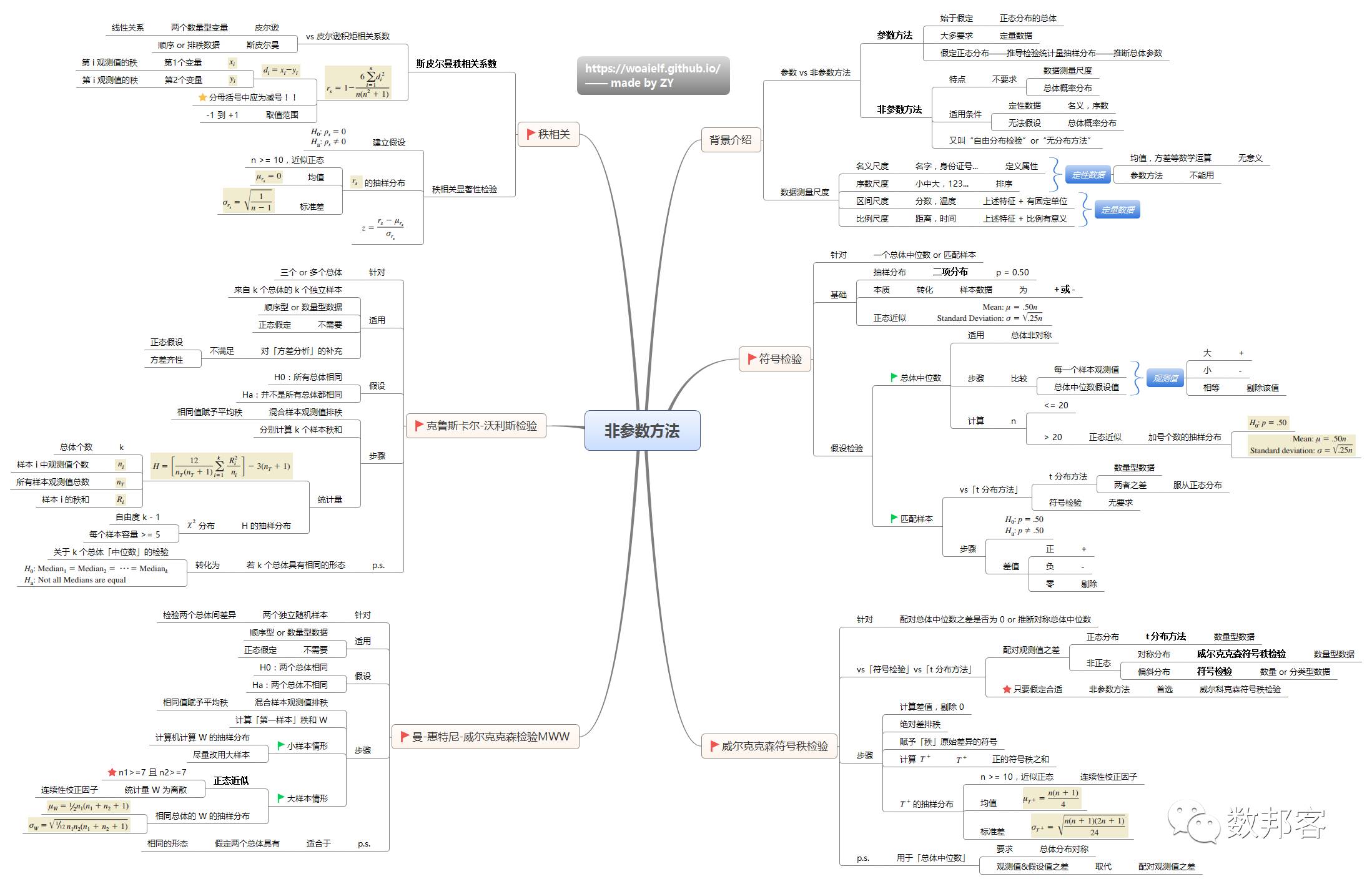
参考资料

《STATISTICS FOR BUSINESS AND ECONOMICS》12e David R. Anderson etc.