牛客网补题 New Game!（原Wannafly summer camp day2原题）

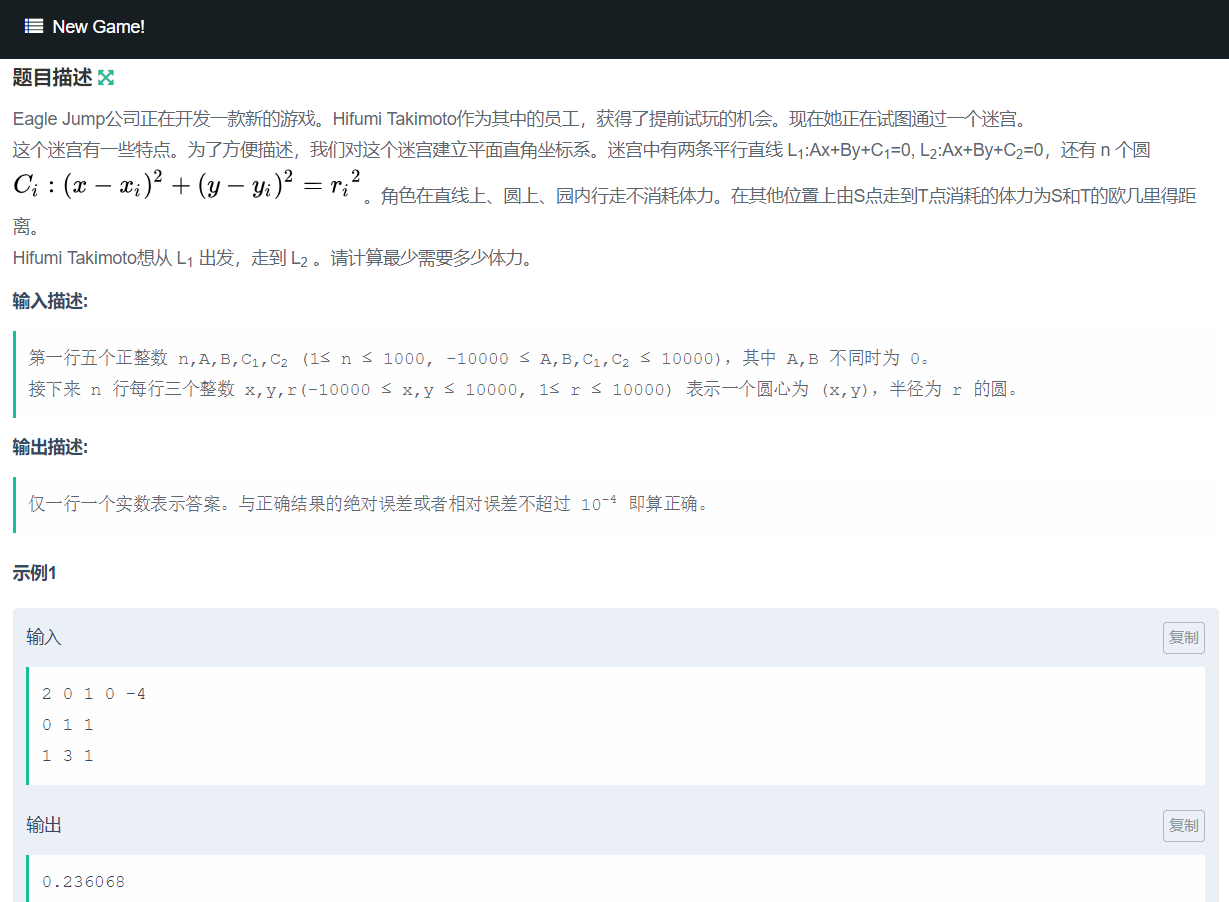
思路：这个题在秦皇岛的时候好像没有写出来，反正我是没有写出来，题解是听懂了；把直线和圆都看做一个结点，圆和直线用点到直线的距离与半径差求出来，圆和圆之间用点和点之间的距离和半径差表示，最后最短路跑一遍就行了。

#include<cstdio>
#include<vector>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
int vis[];
double mlen[];
const double maxn = 1e9 + ;
double map[][];
int n, a, b, c1, c2;
struct Node{
    int x, y, r;
    Node(){}
    Node(int _x, int _y, int _r) :x(_x), y(_y), r(_r){}
}ya[];

void dijkstra(){
    memset(vis, , sizeof vis);

    for (int i = ; i <= n + ; i++)
        mlen[i] = map[][i];
    mlen[] = ;
    /*for (int i = 0; i <= n + 1; i++)
        cout << mlen[i] << " * ";
        */
    for (int t = ; t <= n + ; t++){
        double ma = maxn; int p;
        for (int i = ; i <= n + ; i++){
            if (mlen[i] <= ma&&!vis[i]){ ma = mlen[i]; p = i; }
        }
        vis[p] = ;
        //cout << mlen[p] << " " << p << endl;
        for (int i = ; i <= n + ; i++){
            if (p != i&&!vis[i] && mlen[p] + map[p][i] < mlen[i]){
                mlen[i] = mlen[p] + map[p][i];
                //cout << p << " " << i << " " << mlen[i] << endl;
            }
        }
    }
}
int main(){

    //memset(map, maxn, sizeof map);

    vector<Node>vec;

    scanf("%d%d%d%d%d", &n, &a, &b, &c1, &c2);

    map[][n + ] = map[n + ][] = abs(c1 - c2)*1.0 / sqrt(a*a + b*b);
    for (int i = ; i <= n + ; i++)
    for (int j = ; j <= n + ; j++)
        map[i][j] = maxn;

    int x, y, r;
    for (int i = ; i <= n; i++){
        scanf("%d%d%d", &x, &y, &r);
        vec.push_back(Node(x, y, r));
    }

    for (int i = ; i < vec.size(); i++){
        double len = abs(a*vec[i].x + b*vec[i].y + c1)*1.0 / sqrt(a*a + b*b) - vec[i].r*1.0;
        if (len < )len = ;
        map[][i + ] = len;
        map[i + ][] = len;
    }
    for (int i = ; i < vec.size(); i++){
        double len = abs(a*vec[i].x + b*vec[i].y + c2)*1.0 / sqrt(a*a + b*b) - vec[i].r*1.0;
        if (len < )len = ;
        map[n+][i + ] = len;
        map[i + ][n+] = len;
    }

    for (int i = ; i < n; i++){
        for (int j = i + ; j < n; j++){
            double len = sqrt(pow(vec[i].x - vec[j].x, ) + pow(vec[i].y - vec[j].y, ));
            len = len - vec[i].r - vec[j].r;
            if (len < )len = ;
            map[i + ][j + ] = len;
            map[j + ][i + ] = len;
        }
    }
    /*for (int i = 0; i <= n + 1; i++){
        for (int j = 0; j <= n + 1; j++)
            cout << map[i][j] << " ";
        cout << endl;
    }*/
    dijkstra();
    printf("%.6lf\n", mlen[n + ]);

    return ;
}