【BZOJ 4555】 4555: [Tjoi2016&Heoi2016]求和 （NTT）

4555: [Tjoi2016&Heoi2016]求和

Time Limit: 40 Sec  Memory Limit: 128 MB
Submit: 315  Solved: 252

Description

在2016年，佳媛姐姐刚刚学习了第二类斯特林数，非常开心。

现在他想计算这样一个函数的值:

S(i, j)表示第二类斯特林数，递推公式为:

S(i, j) = j ∗ S(i − 1, j) + S(i − 1, j − 1), 1 <= j <= i − 1。

边界条件为：S(i, i) = 1(0 <= i), S(i, 0) = 0(1 <= i)

你能帮帮他吗?

Input

输入只有一个正整数

Output

输出f(n)。由于结果会很大，输出f(n)对998244353(7 × 17 × 223 + 1)取模的结果即可。1 ≤ n ≤ 100000

Sample Input

3

Sample Output

87

HINT

Source

【分析】

　　额。。要用第二类斯特林数的展开式？

　　表示并不会。于是看题解。ORZ。。ATP大神

　　

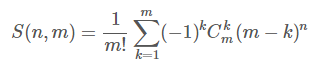
　　带进去，注意不用管j从1到i，因为j从1到n的话后面都是0，没有关系的。

　　最后化成

　　

　　一脸卷积么？个人认为还不是很能看出来。

　　但是，就是！

　　

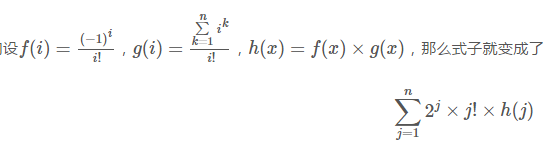
　　h用NTT求，然后求和即可。

　　再次ORZ。。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 #define Maxn 500010
 #define LL long long
 const int Mod=;
 const int G=;

 int a[Maxn],b[Maxn],fac[Maxn];

 int qpow(int x,int b)
 {
     int ans=;
     while(b)
     {
         if(b&) ans=1LL*ans*x%Mod;
         x=1LL*x*x%Mod;
         b>>=;
     }
     return ans;
 } 

 int nn,R[Maxn],inv;
 void ntt(int *s,int f)
 {
     for(int i=;i<nn;i++) if(i<R[i]) swap(s[i],s[R[i]]);
     for(int i=;i<nn;i<<=)
     {
         int wn=qpow(G,(Mod-)/(i<<));
         for(int j=;j<nn;j+=(i<<))
         {
             int w=;
             for(int k=;k<i;k++)
             {
                 int x=s[j+k],y=1LL*w*s[j+k+i]%Mod;
                 s[j+k]=(x+y)%Mod;s[j+k+i]=((x-y)%Mod+Mod)%Mod;
                 w=1LL*w*wn%Mod;
             }
         }
     }
     if(f==-)
     {
         reverse(s+,s+nn);
         for(int i=;i<=nn;i++) s[i]=1LL*s[i]*inv%Mod;
     }
 }

 int main()
 {
     int n;
     scanf("%d",&n);
     fac[]=;for(int i=;i<=n;i++) fac[i]=1LL*i*fac[i-]%Mod;
     for(int i=;i<=n;i++)
     {
         a[i]=qpow(fac[i],Mod-);
         if(i&) a[i]=Mod-a[i];
         b[i]=(-qpow(i,n+))%Mod;
         b[i]=1LL*b[i]*qpow(-i,Mod-)%Mod;
         b[i]=1LL*b[i]*qpow(fac[i],Mod-)%Mod;
         b[i]=(b[i]%Mod+Mod)%Mod;
     }
     nn=;int ll=;
     while(nn<=*n) nn<<=,ll++;
     for(int i=;i<=nn;i++) R[i]=(R[i>>]>>)|((i&)<<(ll-));
     inv=qpow(nn,Mod-);
     b[]=n+;
     ntt(a,);ntt(b,);
     for(int i=;i<=nn;i++) a[i]=1LL*a[i]*b[i]%Mod;
     ntt(a,-);
     int ans=;
     for(int i=;i<=n;i++) ans=(ans+1LL*a[i]*qpow(,i)%Mod*fac[i])%Mod;
     printf("%d\n",ans);
     return ;
 }

代码只需在FFT基础上修改一点点即可。

对于原根，因为你读题时就知道模数，你可以自己打个暴力求一下。具体方法在FFT和NTT总结中有说。

然后你直接赋值原根G的值就好了。

2017-04-14 15:10:42