CodeForces 577E Points on Plane(莫队思维题)

题目描述

On a plane are nn points ( x_{i}xi​ , y_{i}yi​ ) with integer coordinates between 00 and 10^{6}106 . The distance between the two points with numbers aa and bb is said to be the following value: 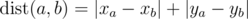 (the distance calculated by such formula is called Manhattan distance).

We call a hamiltonian path to be some permutation p_{i}pi​ of numbers from 11 to nn . We say that the length of this path is value .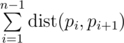

Find some hamiltonian path with a length of no more than 25×10^{8}25×108 . Note that you do not have to minimize the path length.

输入输出格式

输入格式：

 

The first line contains integer nn ( 1<=n<=10^{6}1<=n<=106 ).

The i+1i+1 -th line contains the coordinates of the ii -th point: x_{i}xi​ and y_{i}yi​ ( 0<=x_{i},y_{i}<=10^{6}0<=xi​,yi​<=106 ).

It is guaranteed that no two points coincide.

 

输出格式：

 

Print the permutation of numbers p_{i}pi​ from 11 to nn — the sought Hamiltonian path. The permutation must meet the inequality .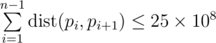

If there are multiple possible answers, print any of them.

It is guaranteed that the answer exists.

 

输入输出样例

输入样例#1：

5
0 7
8 10
3 4
5 0
9 12

输出样例#1：

4 3 1 2 5

说明

In the sample test the total distance is:

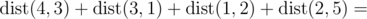
(|5-3|+|0-4|)+(|3-0|+|4-7|)+(|0-8|+|7-10|)+(|8-9|+|10-12|)=2+4+3+3+8+3+1+2=26(∣5−3∣+∣0−4∣)+(∣3−0∣+∣4−7∣)+(∣0−8∣+∣7−10∣)+(∣8−9∣+∣10−12∣)=2+4+3+3+8+3+1+2=26

题意：定义曼哈顿距离为两点之间x坐标差的绝对值与y坐标差的绝对值，在定义哈密顿路径为所有相邻两点间的曼哈顿距离之和，给出一些点的xy坐标，求一个点排列使哈密顿路径小于25*1e8

题解：

首先看到点的xy坐标均在1e6以内，然后如果按照直接优先x再y的顺序排序，只需要一组x坐标1-5e5的数据，每个x坐标的y坐标为1e6和0，然后距离就被卡到了5e11。

虽然上面的思想有错误，但是是有借鉴意义的，如果将哈密顿路径理解为复杂度，长度理解为变量，这显然是n^2的，然后你会想到一些优化的方法，比如说莫队。

然后就可以根据莫队的思想将x坐标分块，分成0-999,1000-1999……的1000块，每块里按照y从小到大的顺序排序，这样子块内y是单调递增的，最多增大1e6，x就算上下乱跳，也最多变化1e3*1e3=1e6，总变化最多2e9

但是还是有点锅，就是块与块之间切换的时候，如果是从最大y切到下一坐标最小y，最多要跳1e6，总变化会多增加1e9

所以按照一个块y递增，下一个块y递减的顺序排列，这样子就稳了

代码如下：

#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

struct node
{
    int x,y,kd;
};

vector<node> g[];
int n;

int cmp1(node x,node y)
{
    return x.y<y.y;
}

int cmp2(node x,node y)
{
    return x.y>y.y;
}

int main()
{
    node tmp;
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%d%d",&tmp.x,&tmp.y);
        tmp.kd=i;
        g[tmp.x/].push_back(tmp);
    }
    for(int i=;i<=;i++)
    {
        if(i&)
        {
            sort(g[i].begin(),g[i].end(),cmp1);
        }
        else
        {
            sort(g[i].begin(),g[i].end(),cmp2);
        }
    }
    for(int i=;i<=;i++)
    {
        for(int j=;j<g[i].size();j++)
        {
            printf("%d ",g[i][j].kd);
        }
    }
}