OpenCV学习(15) 细化算法(3)

      本章我们学习一下Hilditch算法的基本原理，从网上找资料的时候，竟然发现两个有很大差别的算法描述，而且都叫Hilditch算法。不知道那一个才是正宗的，两个算法实现的效果接近，第一种算法更好一些。

第一种算法描述参考paper和代码：

Linear Skeletons from Square Cupboards

Speedup Method for Real-Time Thinning Algorithm

http://cis.k.hosei.ac.jp/~wakahara/Hilditch.c

第二种算法描述参考资料：

http://cgm.cs.mcgill.ca/~godfried/teaching/projects97/azar/skeleton.html#algorithm

 

下面我们分别看一下这两种算法描述：

一、第一种算法描述

假设当前被处理的像素为p0，我们使用下图所示的8邻域表示方式。

     我们处理的为二值图像，背景为黑色，值为0，要细化的前景物体像素值为255。

     对于Hilditch算法来说，它并不是一个完全的并行算法，而是串行并行相结合。当前像素是否是能够删除的骨架点，不仅是由它周围的8邻域决定，而且和前面像素的判定结果有关。一个像素判定为可以删除，我们并不直接删除它，而是在目地图像中设置像素值为GRAY=128,这个信息可能会影响之后其它像素的判定。

      当图像一次扫描迭代完成后，我们把所有置为GRAY的像素设置为0，从而删除它。

 

算法的描述如下。

迭代扫描当前图像

    对于当前像素点，扫描它的8邻域，如果邻域的像素值为255，则b[i]=1(i=0…8)，像素值为128(GRAY，表示该像素点在前面的循环中被标记为删除)，b[i]=-1，如果像素值为0，则b[i]=0。

下面会根据b[i]的值进行6个条件判断，如果条件满足，则会标记该像素值为GRAY(128)。

1. b[0]=1，即当前像素必须为前景点。

2. 1-abs(b1) + 1 – abs(b3) + 1 – abs(b5) + 1 – abs(b7) >= 1，该条件表示当前像素为边界点，即东西南北四个点至少有一个b[i]=0。

3. abs(b1)+…+abs(b8)>=2， 该条件表示不能删除端点，即p0点周围只有一个点为1或-1的情况。

4.  统计b1到b8等于1的数量，该数量值必须大于1，该条件表示不能删除端点。、

5.  连通性检测，使用下面的公式：首先根据当前像素周围3*3域的值，记录d[9]数组，如果b[i]等于0，则d[i]=0， 否则d[i]=1，最后计算 d1-d1*d2*d3+d3-d3*d4*d5+d5-d5*d6*d7+d7-d7*d8*d1是否为1，为1则满足连通性，可以删除。

6.最后一个条件保证当轮廓是2个像素宽时，只删除一边。统计sum的值，当值为8时候，可以删除。

sum = 0;
for (i = 1; i <= 8; i++)
{
    if (b[i] != -1)
    {
        sum++;
    } else
    {
        copy = b[i];
        b[i] = 0;
        if (func_nc8(b) == 1) sum++;
        b[i] = copy;
    }

     当这6个条件都满足时候，标记当前像素值为GRAY(128)，然后在判断别的像素。当所有像素都扫描一遍后，完成一次迭代。

此时我们会把刚才标记为GARY的像素，都设置为0，真正的删除它，如果上一次循环已经没有标记删除的像素，则退出迭代，否则进行下一次迭代。

算法代码：

int gThin::func_nc8(int *b)
    //端点的连通性检测
{
    int n_odd[4] = { 1, 3, 5, 7 };  //四邻域
    int i, j, sum, d[10];          

    for (i = 0; i <= 9; i++) {
        j = i;
        if (i == 9) j = 1;
        if (abs(*(b + j)) == 1)
        {
            d[i] = 1;
        } 
        else 
        {
            d[i] = 0;
        }
    }
    sum = 0;
    for (i = 0; i < 4; i++)
    {
        j = n_odd[i];
        sum = sum + d[j] - d[j] * d[j + 1] * d[j + 2];
    }
    return (sum);
}

void gThin::cvHilditchThin(cv::Mat& src, cv::Mat& dst)
{
    if(src.type()!=CV_8UC1)
    {
        printf("只能处理二值或灰度图像\n");
        return;
    }
    //非原地操作时候，copy src到dst
    if(dst.data!=src.data)
    {
        src.copyTo(dst);
    }

    //8邻域的偏移量
    int offset[9][2] = {{0,0},{1,0},{1,-1},{0,-1},{-1,-1},
    {-1,0},{-1,1},{0,1},{1,1} };
    //四邻域的偏移量
    int n_odd[4] = { 1, 3, 5, 7 };      
    int px, py;                        
    int b[9];                      //3*3格子的灰度信息
    int condition[6];              //1-6个条件是否满足
    int counter;                   //移去像素的数量
    int i, x, y, copy, sum;      

    uchar* img;
    int width, height;
    width = dst.cols;
    height = dst.rows;
    img = dst.data;
    int step = dst.step ;
    do
    {

        counter = 0;

        for (y = 0; y < height; y++)
        {

            for (x = 0; x < width; x++) 
            {

                //前面标记为删除的像素，我们置其相应邻域值为-1
                for (i = 0; i < 9; i++) 
                {
                    b[i] = 0;
                    px = x + offset[i][0];
                    py = y + offset[i][1];
                    if (px >= 0 && px < width &&    py >= 0 && py <height) 
                    {
                        // printf("%d\n", img[py*step+px]);
                        if (img[py*step+px] == WHITE)
                        {
                            b[i] = 1;
                        } 
                        else if (img[py*step+px]  == GRAY) 
                        {
                            b[i] = -1;
                        }
                    }
                }
                for (i = 0; i < 6; i++)
                {
                    condition[i] = 0;
                }

                //条件1，是前景点
                if (b[0] == 1) condition[0] = 1;

                //条件2，是边界点
                sum = 0;
                for (i = 0; i < 4; i++) 
                {
                    sum = sum + 1 - abs(b[n_odd[i]]);
                }
                if (sum >= 1) condition[1] = 1;

                //条件3， 端点不能删除
                sum = 0;
                for (i = 1; i <= 8; i++)
                {
                    sum = sum + abs(b[i]);
                }
                if (sum >= 2) condition[2] = 1;

                //条件4， 孤立点不能删除
                sum = 0;
                for (i = 1; i <= 8; i++)
                {
                    if (b[i] == 1) sum++;
                }
                if (sum >= 1) condition[3] = 1;

                //条件5， 连通性检测
                if (func_nc8(b) == 1) condition[4] = 1;

                //条件6，宽度为2的骨架只能删除1边
                sum = 0;
                for (i = 1; i <= 8; i++)
                {
                    if (b[i] != -1) 
                    {
                        sum++;
                    } else 
                    {
                        copy = b[i];
                        b[i] = 0;
                        if (func_nc8(b) == 1) sum++;
                        b[i] = copy;
                    }
                }
                if (sum == 8) condition[5] = 1;

                if (condition[0] && condition[1] && condition[2] &&condition[3] && condition[4] && condition[5])
                {
                    img[y*step+x] = GRAY; //可以删除，置位GRAY，GRAY是删除标记，但该信息对后面像素的判断有用
                    counter++;
                    //printf("----------------------------------------------\n");
                    //PrintMat(dst);
                }
            } 
        }

        if (counter != 0)
        {
            for (y = 0; y < height; y++)
            {
                for (x = 0; x < width; x++)
                {
                    if (img[y*step+x] == GRAY)
                        img[y*step+x] = BLACK;

                }
            }
        }

    }while (counter != 0);

}

二、第二种算法描述

       第二种算法描述和Zhang的并行算法很相似，特别是前2个条件一模一样，不同的是3，4两个条件，还有就是该描述算法并没有像zhang算法那样，把一次迭代分成2个阶段。

此时我们使用的8邻域标记为：

下面看下它的算法描述：

复制目地图像到临时图像，对临时图像进行一次扫描，对于不为0的点，如果满足以下四个条件，则在目地图像中删除该点(就是设置该像素为0)

a. 2<= p2+p3+p4+p5+p6+p7+p8+p9<=6

    大于等于2会保证p1点不是端点或孤立点，因为删除端点和孤立点是不合理的，小于等于6保证p1点是一个边界点，而不是一个内部点。等于0时候，周围没有等于1的像素，所以p1为孤立点，等于1的时候，周围只有1个灰度等于1的像素，所以是端点（注：端点是周围有且只能有1个值为1的像素)。

b. p2->p9的排列顺序中，01模式的数量为1，比如下面的图中，有p2p3 => 01, p6p7=>01,所以该像素01模式的数量为2。

  之所以要01模式数量为1，是要保证删除当前像素点后的连通性。比如下面的图中，01模式数量大于1，如果删除当前点p1，则连通性不能保证。

 

c. p2.p4.p8 = 0 or A(p2)!=1，A(p2)表示p2周围8邻域的01模式和。这个条件保证2个像素宽的垂直条不完全被腐蚀掉。

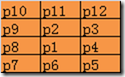
d.p2.p4.p6 = 0 or A(p4)!=1，A(p4)表示p4周围8邻域的01模式和。这个条件保证2个像素宽的水平条不完全被腐蚀掉。

算法代码：

void gThin::cvHilditchThin1(cv::Mat& src, cv::Mat& dst)
{
    //http://cgm.cs.mcgill.ca/~godfried/teaching/projects97/azar/skeleton.html#algorithm
    //算法有问题，得不到想要的效果
    if(src.type()!=CV_8UC1)
    {
        printf("只能处理二值或灰度图像\n");
        return;
    }
    //非原地操作时候，copy src到dst
    if(dst.data!=src.data)
    {
        src.copyTo(dst);
    }

    int i, j;
    int width, height;
    //之所以减2，是方便处理8邻域，防止越界
    width = src.cols -2;
    height = src.rows -2;
    int step = src.step;
    int  p2,p3,p4,p5,p6,p7,p8,p9;
    uchar* img;
    bool ifEnd;
    int A1;
    cv::Mat tmpimg;
    while(1)
    {
        dst.copyTo(tmpimg);
        ifEnd = false;
        img = tmpimg.data+step;
        for(i = 2; i < height; i++)
        {
            img += step;
            for(j =2; j<width; j++)
            {
                uchar* p = img + j;
                A1 = 0;
                if( p[0] > 0)
                {
                    if(p[-step]==0&&p[-step+1]>0) //p2,p3 01模式
                    {
                        A1++;
                    }
                    if(p[-step+1]==0&&p[1]>0) //p3,p4 01模式
                    {
                        A1++;
                    }
                    if(p[1]==0&&p[step+1]>0) //p4,p5 01模式
                    {
                        A1++;
                    }
                    if(p[step+1]==0&&p[step]>0) //p5,p6 01模式
                    {
                        A1++;
                    }
                    if(p[step]==0&&p[step-1]>0) //p6,p7 01模式
                    {
                        A1++;
                    }
                    if(p[step-1]==0&&p[-1]>0) //p7,p8 01模式
                    {
                        A1++;
                    }
                    if(p[-1]==0&&p[-step-1]>0) //p8,p9 01模式
                    {
                        A1++;
                    }
                    if(p[-step-1]==0&&p[-step]>0) //p9,p2 01模式
                    {
                        A1++;
                    }
                    p2 = p[-step]>0?1:0;
                    p3 = p[-step+1]>0?1:0;
                    p4 = p[1]>0?1:0;
                    p5 = p[step+1]>0?1:0;
                    p6 = p[step]>0?1:0;
                    p7 = p[step-1]>0?1:0;
                    p8 = p[-1]>0?1:0;
                    p9 = p[-step-1]>0?1:0;
                    //计算AP2,AP4
                    int A2, A4;
                    A2 = 0;
                    //if(p[-step]>0)
                    {
                        if(p[-2*step]==0&&p[-2*step+1]>0) A2++;
                        if(p[-2*step+1]==0&&p[-step+1]>0) A2++;
                        if(p[-step+1]==0&&p[1]>0) A2++;
                        if(p[1]==0&&p[0]>0) A2++;
                        if(p[0]==0&&p[-1]>0) A2++;
                        if(p[-1]==0&&p[-step-1]>0) A2++;
                        if(p[-step-1]==0&&p[-2*step-1]>0) A2++;
                        if(p[-2*step-1]==0&&p[-2*step]>0) A2++;
                    }

                    A4 = 0;
                    //if(p[1]>0)
                    {
                        if(p[-step+1]==0&&p[-step+2]>0) A4++;
                        if(p[-step+2]==0&&p[2]>0) A4++;
                        if(p[2]==0&&p[step+2]>0) A4++;
                        if(p[step+2]==0&&p[step+1]>0) A4++;
                        if(p[step+1]==0&&p[step]>0) A4++;
                        if(p[step]==0&&p[0]>0) A4++;
                        if(p[0]==0&&p[-step]>0) A4++;
                        if(p[-step]==0&&p[-step+1]>0) A4++;
                    }

                    //printf("p2=%d p3=%d p4=%d p5=%d p6=%d p7=%d p8=%d p9=%d\n", p2, p3, p4, p5, p6,p7, p8, p9);
                    //printf("A1=%d A2=%d A4=%d\n", A1, A2, A4);
                    if((p2+p3+p4+p5+p6+p7+p8+p9)>1 && (p2+p3+p4+p5+p6+p7+p8+p9)<7  &&  A1==1)
                    {
                        if(((p2==0||p4==0||p8==0)||A2!=1)&&((p2==0||p4==0||p6==0)||A4!=1)) 
                        {
                            dst.at<uchar>(i,j) = 0; //满足删除条件，设置当前像素为0
                            ifEnd = true;
                            //printf("\n");

                            //PrintMat(dst);
                        }
                    }
                }
            }
        }
        //printf("\n");
        //PrintMat(dst);
        //PrintMat(dst);
        //已经没有可以细化的像素了，则退出迭代
        if(!ifEnd) break;
    }
}

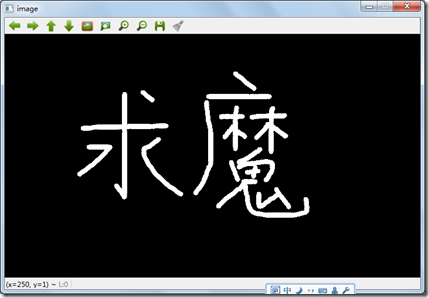
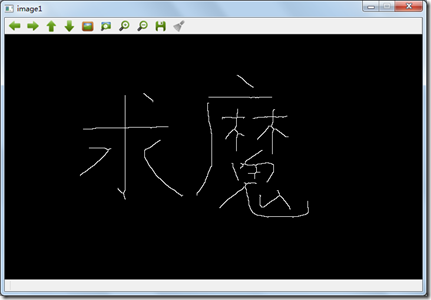
第一种Hilditch算法的结果：

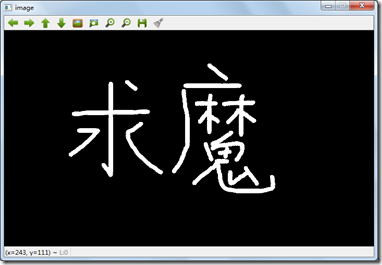
第二种Hilditch算法的结果：

程序代码：工程FirstOpenCV11