【题解】BZOJ 3065: 带插入区间K小值——替罪羊树套线段树

题目传送门

题解

orz vfk的题解

3065: 带插入区间K小值 系列题解

• 一
• 二
• 三
• 四

惨

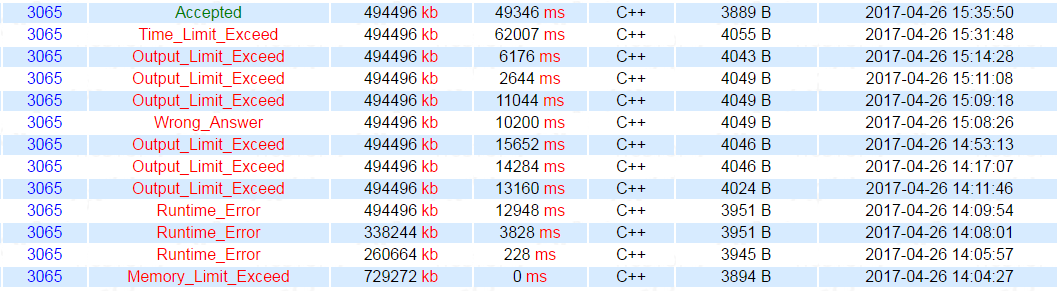
一开始用了一种空间常数很大的方法，每次重构的时候merge两颗线段树，然后无限RE（其实是MLE）。

后来改成枚举子树元素插入，空间缩小为约 \(\frac 1 4\) ，然而TLE。

然后把替罪羊树的 \(\alpha\) 从 0.6改成0.75，就卡过了。

代码

#include <bits/stdc++.h>
using namespace std;
const int MAXN=140005, MAXM=3e7, MAXB=2e7, MX=70000;
const double al=0.75;
char BUF[MAXB], *cp=BUF;
void rd(int &x){
	x=0;
	while(*cp<'0'||'9'<*cp)cp++;
	while('0'<=*cp&&*cp<='9')x=x*10+*cp++-'0';
}
char rc(){while(*cp<'A'||'Z'<*cp)cp++; return *cp++;}
int N, M, L, R, TOP, top, ov;
int nt, tot, ok, A[MAXN];
struct Seg{
	Seg *lc, *rc;
	int s;
	void *operator new(size_t);
	void operator delete(void *);
	Seg();
	void up(){s=lc->s+rc->s;}
}tr[MAXM], *ST[MAXM], *tmp[MAXN];
void *Seg::operator new(size_t size){return ST[--TOP];}
void Seg::operator delete(void *p){ST[TOP++]=(Seg*)p;}
Seg::Seg(){lc=rc=tr;s=0;}
void dec(Seg *&x){
	if(x==tr) return;
	dec(x->lc); dec(x->rc); delete(x); x=tr;
}
void upd(Seg *&x, int l, int r, int k, int v){
	if(x==tr) x=new Seg;
	if(l==r){x->s+=v; return;}
	int mid=(l+r)>>1;
	if(k<=mid) upd(x->lc,l,mid,k,v);
	else upd(x->rc,mid+1,r,k,v);
	x->up();
	if(!x->s) dec(x);
}
struct Node{
	Node *lc, *rc;
	Seg *c, *s;
	int sz, v;
	void up(){sz=1+lc->sz+rc->sz;}
}nd[MAXN], *st[MAXN], *root;
void dfs(Node *x){
	if(x==nd) return; dec(x->s);
	dfs(x->lc); st[top++]=x; dfs(x->rc);
}
void bu(Node *&x, int l, int r){
	if(l>r){x=nd; return;}
	int mid=(l+r)>>1; x=st[mid];
	bu(x->lc,l,mid-1); bu(x->rc,mid+1,r);
	x->up();
	for(int i=l; i<=r; ++i) upd(x->s,0,MX,st[i]->v,1);
}
void rebu(Node *&x){top=0; dfs(x); bu(x,0,top-1);}
void ins(Node *&x, int k, int v, int d=0){
	if(x==nd){
		x=&nd[++tot]; x->v=v;
		upd(x->c,0,MX,v,1);
		upd(x->s,0,MX,v,1);
		return;
	}
	upd(x->s,0,MX,v,1);
	int t=x->lc->sz+1;
	if(k<=t){
		ins(x->lc,k,v,d+1); x->up();
		if(x->lc->sz>=al*x->sz) rebu(x);
	}else{
		ins(x->rc,k-t,v,d+1); x->up();
		if(x->rc->sz>=al*x->sz) rebu(x);
	}
}
void md(Node *&x, int k, int v){
	if(x==nd) return;
	int t=x->lc->sz;
	if(k==t+1){
		ov=x->v; x->v=v;
		dec(x->c); upd(x->c,0,MX,v,1);
	}else if(k<=t) md(x->lc,k,v);
	else md(x->rc,k-t-1,v);
	upd(x->s,0,MX,ov,-1);
	upd(x->s,0,MX,v,1);
}
void qry(Node *x, int l, int r){
	if(x==nd) return;
	if(L<=l&&r<=R){
		tmp[nt++]=x->s;
		return;
	}
	int t=x->lc->sz;
	if(L<=l+t&&l+t<=R) tmp[nt++]=x->c;
	if(L<l+t) qry(x->lc,l,l+t-1);
	if(l+t<R) qry(x->rc,l+t+1,r);
}
int kth(int k){
	int l=0, r=MX;
	while(l<r){
		int t=0, mid=(l+r)>>1;
		for(int i=0; i<nt; ++i) t+=tmp[i]->lc->s;
		if(k<=t){
			r=mid;
			for(int i=0; i<nt; ++i) tmp[i]=tmp[i]->lc;
		}else{
			l=mid+1; k-=t;
			for(int i=0; i<nt; ++i) tmp[i]=tmp[i]->rc;
		}
	}
	return l;
}
void init(){
	tr[0].lc=tr[0].rc=tr;
	for(int i=MAXM-1; i>0; --i) ST[TOP++]=tr+i;
	root=nd[0].lc=nd[0].rc=nd;
	nd[0].c=nd[0].s=tr;
	for(int i=1; i<MAXN; ++i){
		nd[i].c=nd[i].s=tr;
		nd[i].lc=nd[i].rc=nd;
		nd[i].sz=1;
	}
	for(int i=1; i<=N; ++i){
		upd(nd[i].c,0,MX,A[i],1);
		st[top++]=nd+i; nd[i].v=A[i];
	}
	bu(root,0,top-1); tot=N;
}
int main(){
	fread(BUF, 1, MAXB, stdin);rd(N);
	for(int i=1; i<=N; ++i) rd(A[i]);
	init(); rd(M);int last=0;
	while(M--){
		char ch=rc();
		int x,y,k; rd(x),rd(y);
		x^=last; y^=last;
		if(ch=='Q'){
			L=x, R=y;
			rd(k); k^=last;
			nt=0; qry(root,1,N);
			printf("%d\n", last=kth(k));
		}else if(ch=='M')md(root,x,y);
		else if(ch=='I')ins(root,x,y),N++;
	}
	return 0;
}