图 Graph-图的相关算法
2018-03-06 17:42:02
一、最短路问题
问题描述:在网络中,求两个不同顶点之间的所有路径中,边的权值之和最小的那一条路径。
- 这条路径就是两点之间的最短路径 (Shortest Path)
- 第一个顶点为源点 (Source)
- 最后一个顶点为终点 (Destination)
问题分类:
- 单源最短路径问题:从某固定源点出发,求其到所有其他顶点的最短路径。
- (有向)无权图
- (有向)有权图
- 多源最短路径问题:求任意两顶点间的最短路径。
1)无权图的单源最短路算法
BFS可以解决这类问题。
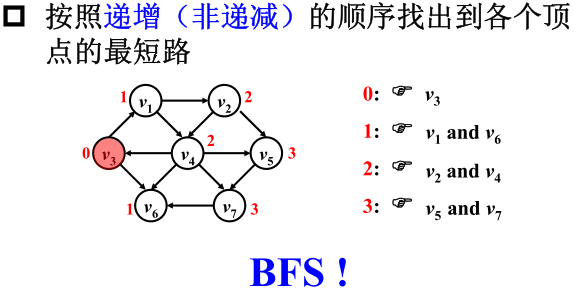

2)有权图的单源最短路算法
Dijkstra算法可以解决不带负值边的单源最短路问题。



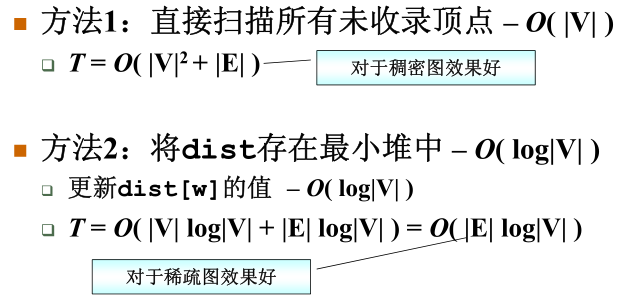
3)多源最短路算法
此算法由Robert W. Floyd(罗伯特·弗洛伊德)于1962年发表在“Communications of the ACM”上。同年Stephen Warshall(史蒂芬·沃舍尔)也独立发表了这个算法。Floyd这个牛人是朵奇葩,他原本在芝加哥大学读的文学,但是因为当时美国经济不太景气,找工作比较困难,无奈之下到西屋电气公司当了一名计算机操作员,在IBM650机房值夜班,并由此开始了他的计算机生涯。
我们来想一想,根据我们以往的经验,如果要让任意两点(例如从顶点a点到顶点b)之间的路程变短,只能引入第三个点(顶点k),并通过这个顶点k中转即a->k->b,才可能缩短原来从顶点a点到顶点b的路程。那么这个中转的顶点k是1~n中的哪个点呢?甚至有时候不只通过一个点,而是经过两个点或者更多点中转会更短,即a->k1->k2b->或者a->k1->k2…->k->i…->b。比如上图中从4号城市到3号城市(4->3)的路程e[4][3]原本是12。如果只通过1号城市中转(4->1->3),路程将缩短为11(e[4][1]+e[1][3]=5+6=11)。其实1号城市到3号城市也可以通过2号城市中转,使得1号到3号城市的路程缩短为5(e[1][2]+e[2][3]=2+3=5)。所以如果同时经过1号和2号两个城市中转的话,从4号城市到3号城市的路程会进一步缩短为10。通过这个的例子,我们发现每个顶点都有可能使得另外两个顶点之间的路程变短。
Floyd算法就是首先只允许经过0号结点,看看是否会变短,如果变短就加之修改,然后只允许经过0,1号结点,看看是否变短,加之修改,直到中间结点到达为所有可能的结点。


二、最小生成树 (Minimum Spanning Tree)
什么是最小生成树?

最小生成树算法使用贪心的思想,每一步都选权重最小的边。

- Prim算法 — 让一棵小树长大
首先随机选择起始点,然后不断将当前结点往外生长,寻找最短的结点加入。

- Kruskal算法 — 将森林合并成树

三、拓扑排序
拓扑序:如果图中从V到W有一条有向路径,则V一定排在W之前。满足此条件的顶点序列称为一个拓扑序。
获得一个拓扑序的过程就是拓扑排序。
AOV(Activity On Vertex)如果有合理的拓扑序,则必定是有向无环图(Directed Acyclic Graph, DAG)。
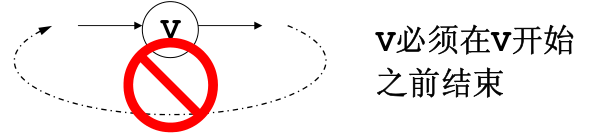
举个例子,将计算机学院的课程按照拓扑序进行输出。

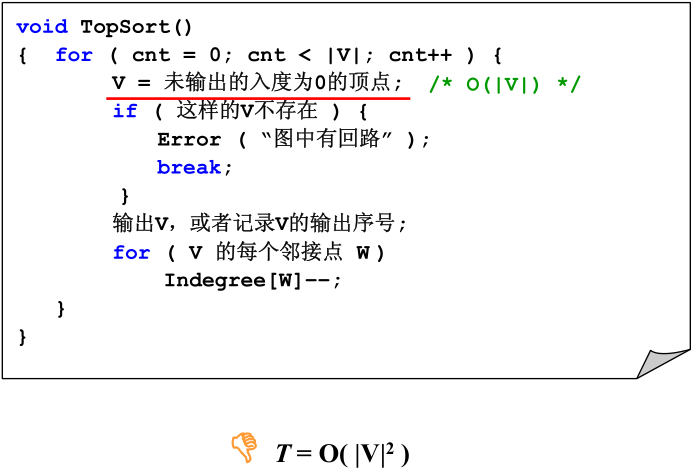
一种聪明的算法就是将入度为0的结点放到队列。

关键路径问题:

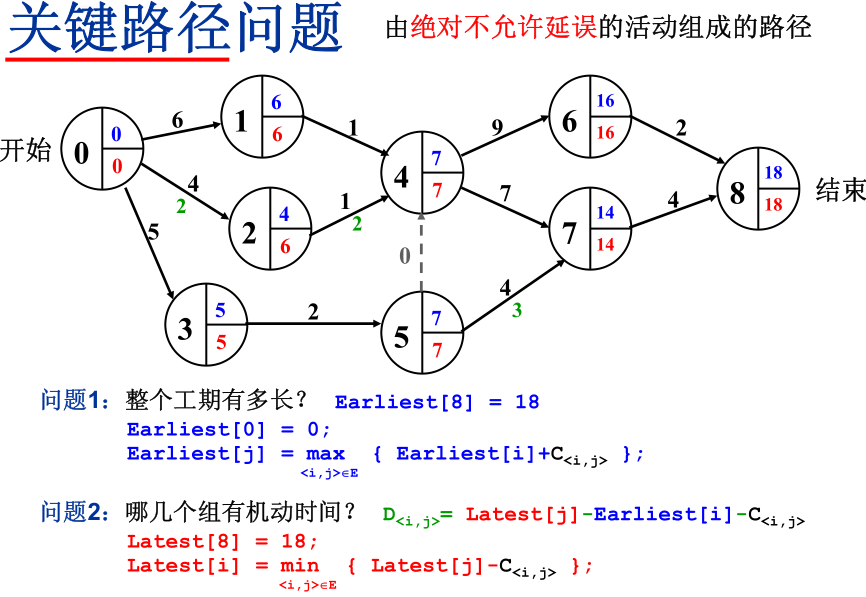
图 Graph-图的相关算法的更多相关文章
- 算法与数据结构基础 - 图(Graph)
图基础 图(Graph)应用广泛,程序中可用邻接表和邻接矩阵表示图.依据不同维度,图可以分为有向图/无向图.有权图/无权图.连通图/非连通图.循环图/非循环图,有向图中的顶点具有入度/出度的概念. 面 ...
- 【数据结构与算法Python版学习笔记】图——基本概念及相关术语
概念 图Graph是比树更为一般的结构, 也是由节点和边构成 实际上树是一种具有特殊性质的图 图可以用来表示现实世界中很多有意思的事物,包括道路系统.城市之间的航班.互联网的连接,甚至是计算机专业的一 ...
- 关于图计算&图学习的基础知识概览:前置知识点学习(Paddle Graph Learning (PGL))
关于图计算&图学习的基础知识概览:前置知识点学习(Paddle Graph Learning (PGL)) 欢迎fork本项目原始链接:关于图计算&图学习的基础知识概览:前置知识点学习 ...
- 纸上谈兵: 图 (graph)
作者:Vamei 出处:http://www.cnblogs.com/vamei 欢迎转载,也请保留这段声明.谢谢! 图(graph)是一种比较松散的数据结构.它有一些节点(vertice),在某些节 ...
- C++编程练习(10)----“图的最小生成树“(Prim算法、Kruskal算法)
1.Prim 算法 以某顶点为起点,逐步找各顶点上最小权值的边来构建最小生成树. 2.Kruskal 算法 直接寻找最小权值的边来构建最小生成树. 比较: Kruskal 算法主要是针对边来展开,边数 ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (二)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- MATLAB实例:求相关系数、绘制热图并找到强相关对
MATLAB实例:求相关系数.绘制热图并找到强相关对 作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 用MATLAB编程,求给定数据不同维度之间的相关系 ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (三)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 看图轻松理解数据结构与算法系列(NoSQL存储-LSM树) - 全文
<看图轻松理解数据结构和算法>,主要使用图片来描述常见的数据结构和算法,轻松阅读并理解掌握.本系列包括各种堆.各种队列.各种列表.各种树.各种图.各种排序等等几十篇的样子. 关于LSM树 ...
随机推荐
- 多个JS文件性能优化
页面中引入的JS文件是阻塞式加载的,这样会影响页面性能.以下是JS文件性能优化方法: 一:将所有的<script>标签放到页面底部,也就是</body>闭合标签之前,这能确保在 ...
- Selenium2.0 Webdriver 随笔
Webdriver can't action the element when the element is out of view 1. Scroll to the element use Java ...
- ubuntu 16.4安装卸载apache+php+mysql
1.安装apache sudo apt-get update sudo apt-get install apache2 2.安装php5.6 添加PPA源:add-apt-repository ppa ...
- 利用page_source抓取网页中的URL,进行链接测试
selenium的page_source方法可以获取到页面源码,下面就把它应用到链接测试中. # coding:utf-8 __author__ = 'helen' import re,request ...
- SSIS 2012 Error: An Integration Services class cannot be found
升级SSIS到SQL Server 2012,服务器只安装了SSIS一个功能,应用程序执行dtsx包时报错如下: An Integration Services class cannot be fou ...
- C语言基础温故
一.C语言中数组动态增长有哪些方法? 1.在原数组单元后面是没法再扩长的,因为后面的单元没法保证一定有.所以,数组原址动态增长肯定是不行的: 2.要么定义长一点的数组,要么自已把N个数组用链表串起来, ...
- 如何禁止ping
PING命令是个危险的命令,用它可以知道你的操作系统,IP等,为了安全禁PING是个很好的方法,也是防DDOS攻击的.应该是有外部网络试图连接你的UDP的1434端口,不知道你打了补丁没有. 黑客入侵 ...
- 《Java程序设计》实验4
20145318 <Java程序设计>实验4 实验内容 安装Android Studio 运行安卓AVD模拟器 使用Android运行出模拟手机并显示自己的学号 实验过程 安装Androi ...
- 怎样让.bat文件直接运行不需要右键管理员权限
:: BatchGotAdmin :------------------------------------- REM --> Check for permissions >nul 2&g ...
- Redis中RedisTemplate和Redisson管道的使用
当对Redis进行高频次的命令发送时,由于网络IO的原因,会耗去大量的时间.所以Redis提供了管道技术,就是将命令一次性批量的发送给Redis,从而减少IO. 一.Jedis对redis的管道进行操 ...
