图 Graph-图的相关算法
2018-03-06 17:42:02
一、最短路问题
问题描述:在网络中,求两个不同顶点之间的所有路径中,边的权值之和最小的那一条路径。
- 这条路径就是两点之间的最短路径 (Shortest Path)
- 第一个顶点为源点 (Source)
- 最后一个顶点为终点 (Destination)
问题分类:
- 单源最短路径问题:从某固定源点出发,求其到所有其他顶点的最短路径。
- (有向)无权图
- (有向)有权图
- 多源最短路径问题:求任意两顶点间的最短路径。
1)无权图的单源最短路算法
BFS可以解决这类问题。
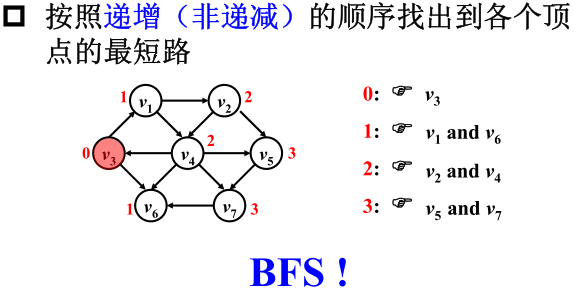

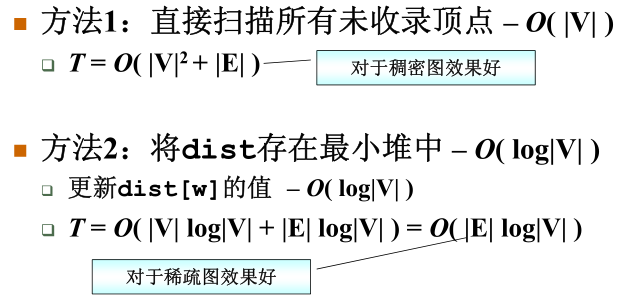
2)有权图的单源最短路算法
Dijkstra算法可以解决不带负值边的单源最短路问题。



3)多源最短路算法
此算法由Robert W. Floyd(罗伯特·弗洛伊德)于1962年发表在“Communications of the ACM”上。同年Stephen Warshall(史蒂芬·沃舍尔)也独立发表了这个算法。Floyd这个牛人是朵奇葩,他原本在芝加哥大学读的文学,但是因为当时美国经济不太景气,找工作比较困难,无奈之下到西屋电气公司当了一名计算机操作员,在IBM650机房值夜班,并由此开始了他的计算机生涯。
我们来想一想,根据我们以往的经验,如果要让任意两点(例如从顶点a点到顶点b)之间的路程变短,只能引入第三个点(顶点k),并通过这个顶点k中转即a->k->b,才可能缩短原来从顶点a点到顶点b的路程。那么这个中转的顶点k是1~n中的哪个点呢?甚至有时候不只通过一个点,而是经过两个点或者更多点中转会更短,即a->k1->k2b->或者a->k1->k2…->k->i…->b。比如上图中从4号城市到3号城市(4->3)的路程e[4][3]原本是12。如果只通过1号城市中转(4->1->3),路程将缩短为11(e[4][1]+e[1][3]=5+6=11)。其实1号城市到3号城市也可以通过2号城市中转,使得1号到3号城市的路程缩短为5(e[1][2]+e[2][3]=2+3=5)。所以如果同时经过1号和2号两个城市中转的话,从4号城市到3号城市的路程会进一步缩短为10。通过这个的例子,我们发现每个顶点都有可能使得另外两个顶点之间的路程变短。
Floyd算法就是首先只允许经过0号结点,看看是否会变短,如果变短就加之修改,然后只允许经过0,1号结点,看看是否变短,加之修改,直到中间结点到达为所有可能的结点。


二、最小生成树 (Minimum Spanning Tree)
什么是最小生成树?

最小生成树算法使用贪心的思想,每一步都选权重最小的边。

- Prim算法 — 让一棵小树长大
首先随机选择起始点,然后不断将当前结点往外生长,寻找最短的结点加入。

- Kruskal算法 — 将森林合并成树

三、拓扑排序
拓扑序:如果图中从V到W有一条有向路径,则V一定排在W之前。满足此条件的顶点序列称为一个拓扑序。
获得一个拓扑序的过程就是拓扑排序。
AOV(Activity On Vertex)如果有合理的拓扑序,则必定是有向无环图(Directed Acyclic Graph, DAG)。
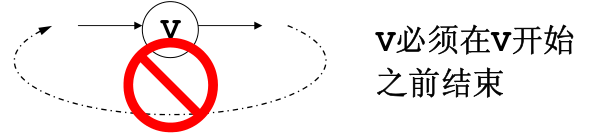
举个例子,将计算机学院的课程按照拓扑序进行输出。

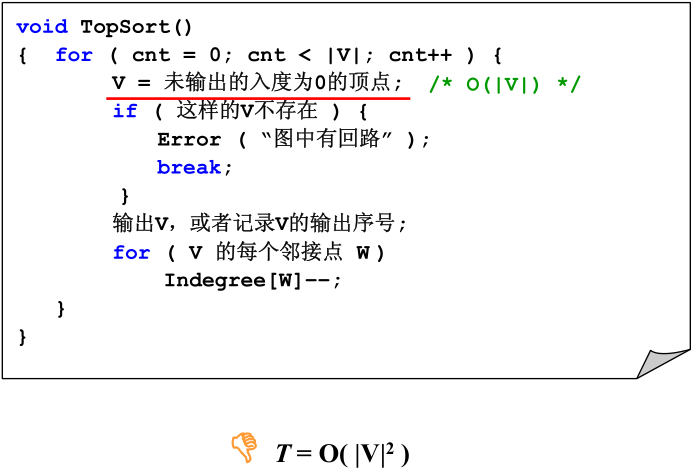
一种聪明的算法就是将入度为0的结点放到队列。

关键路径问题:

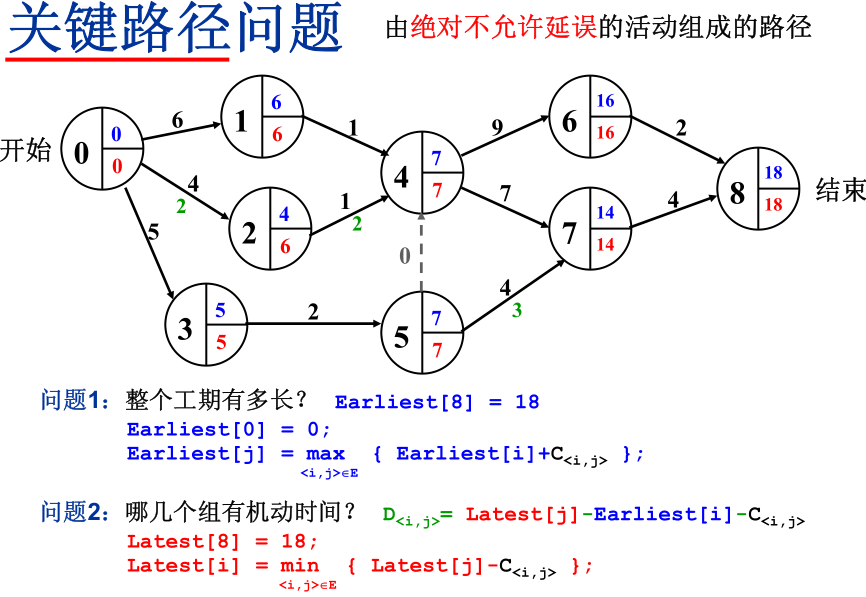
图 Graph-图的相关算法的更多相关文章
- 算法与数据结构基础 - 图(Graph)
图基础 图(Graph)应用广泛,程序中可用邻接表和邻接矩阵表示图.依据不同维度,图可以分为有向图/无向图.有权图/无权图.连通图/非连通图.循环图/非循环图,有向图中的顶点具有入度/出度的概念. 面 ...
- 【数据结构与算法Python版学习笔记】图——基本概念及相关术语
概念 图Graph是比树更为一般的结构, 也是由节点和边构成 实际上树是一种具有特殊性质的图 图可以用来表示现实世界中很多有意思的事物,包括道路系统.城市之间的航班.互联网的连接,甚至是计算机专业的一 ...
- 关于图计算&图学习的基础知识概览:前置知识点学习(Paddle Graph Learning (PGL))
关于图计算&图学习的基础知识概览:前置知识点学习(Paddle Graph Learning (PGL)) 欢迎fork本项目原始链接:关于图计算&图学习的基础知识概览:前置知识点学习 ...
- 纸上谈兵: 图 (graph)
作者:Vamei 出处:http://www.cnblogs.com/vamei 欢迎转载,也请保留这段声明.谢谢! 图(graph)是一种比较松散的数据结构.它有一些节点(vertice),在某些节 ...
- C++编程练习(10)----“图的最小生成树“(Prim算法、Kruskal算法)
1.Prim 算法 以某顶点为起点,逐步找各顶点上最小权值的边来构建最小生成树. 2.Kruskal 算法 直接寻找最小权值的边来构建最小生成树. 比较: Kruskal 算法主要是针对边来展开,边数 ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (二)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- MATLAB实例:求相关系数、绘制热图并找到强相关对
MATLAB实例:求相关系数.绘制热图并找到强相关对 作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 用MATLAB编程,求给定数据不同维度之间的相关系 ...
- 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (三)
本文属于图神经网络的系列文章,文章目录如下: 从图(Graph)到图卷积(Graph Convolution):漫谈图神经网络模型 (一) 从图(Graph)到图卷积(Graph Convolutio ...
- 看图轻松理解数据结构与算法系列(NoSQL存储-LSM树) - 全文
<看图轻松理解数据结构和算法>,主要使用图片来描述常见的数据结构和算法,轻松阅读并理解掌握.本系列包括各种堆.各种队列.各种列表.各种树.各种图.各种排序等等几十篇的样子. 关于LSM树 ...
随机推荐
- python web框架 MVC MTV
WEB框架 MVC Model View Controller 数据库 模板文件 业务处理 MTV Model Template View 数据库 模板文件 业务处理
- CloudFoundry V2 单机版离线安装(伪离线安装)
版权声明:本文为博主原创文章,未经博主同意不得转载. https://blog.csdn.net/wangdk789/article/details/30255763 之前安装CloudFou ...
- byte[]数组和int之间的转换
这里简单记录下两种转换方式: 第一种: 1.int与byte[]之间的转换(类似的byte short,long型) /** * 将int数值转换为占四个字节的byte数组,本方法适用于(低位在前,高 ...
- zabbix详解(一)
zabbix简介 zabbix是一个基于WEB界面的提供分布式系统监视以及网络监视功能的企业级的开源解决方案. zabbix能监视各种网络参数,保证服务器系统的安全运营:并提供柔软的通知机制以让系统管 ...
- 使用DAO工厂创建实现类对象
首先分析DAO模式中的每一部分 VO(对象实体):这个类成员变量与数据库中每个字段一一对应,同时提供了相应是set和get方法来设置或取得数值.这个类一般是通过IDE自动生成的 DAO(数据访问接口) ...
- tomcat 连接器优化
在$CATALINA_HOME/conf/server.xml配置文件中的Connetctor节点,和连接数相关的参数配置和优化. maxThreads Tomcat使用线程来处理接收的每个请求.这个 ...
- 获取Android设备的方向,Sensor和SensorManager实现手机旋转角度
http://www.jcodecraeer.com/a/anzhuokaifa/androidkaifa/2012/1009/425.html 带有g-sensor的Android设备上可通过API ...
- 20145328 《Java程序设计》课程总结
20145328 <Java程序设计>课程总结 每周学习总结链接汇总 20145328 <Java程序设计>第0周学习总结 20145328 <Java程序设计>第 ...
- 33c3-pwn500-recurse
Recurse 好记性不如烂笔头.当时没有记录,现在趁着有时间简单写一写,为以后留备份. 这个题目当时并没有队伍做出来,赛后作者发布了题目的源码和解答.看了之后发现是一个UAF漏洞,不过漏洞很不好找. ...
- Fiddler4调试工具配置使用笔记
Fiddler最大的用处: 模拟请求.修改请求.手机应用调试 Fiddler最新版本 下载地址: http://www.telerik.com/download/fiddler Fiddler 想要监 ...
