【51NOD】1006 最长公共子序列Lcs（动态规划）

给出两个字符串A B，求A与B的最长公共子序列（子序列不要求是连续的）。

比如两个串为：

 

abcicba

abdkscab

 

ab是两个串的子序列，abc也是，abca也是，其中abca是这两个字符串最长的子序列。

Input

第1行：字符串A
第2行：字符串B
(A,B的长度 <= 1000)

Output

输出最长的子序列，如果有多个，随意输出1个。

Input示例

abcicba
abdkscab

Output示例

abca

---

问题定义
• 子序列
– X=(A, B, C, B, D, B)
– Z=(B, C, D, B)是X的子序例
– W=(B, D, A)不是X的子序例
• 公共子序列
–Z是序列X与Y的公共子序列如果Z是X的
子序也是Y的子序列。
最长公共子序列（LCS）问题
输入：X = (x1,x2,...,xn)，Y =
(y1,y2,...ym)
输出：Z = X与Y的最长公共子序
列
最长公共子序列结构分析
• 第i前缀
– 设X=(x1, x2, ..., xn)是一个序列，X的第i前
缀Xi
是一个序列，定义为Xi=(x1, ..., xi )
例. X=(A, B, D, C, A), X1=(A), X2=(A, B), X3=(A,
B, D)
优化子结构
定理1（优化子结构）设X=(x1, ..., xm)、
Y=(y1, ..., yn) 是两个序列，Z=(z1, ..., zk)是X与Y的
LCS，我们有：
⑴ 如果xm=yn, 则zk=xm=yn, Zk-1
是Xm-1
和Yn-1
的
LCS，即，LCSXY = LCSXm-1Yn-1
+ <xm=yn>.
⑵ 如果xm.yn
，且zk.xm
，则Z是Xm-1
和Y的
LCS，即 LCSXY= LCSXm-1Y
⑶ 如果xm.yn,且zk.yn,则Z是X与Yn-1
的LCS，
即 LCSXY= LCSXYn-1
证明:
⑴. X=<x1, …, xm-1, xm>, Y=<y1, …, yn-1, xm>，则
LCSXY = LCSXm-1Yn-1
+ <xm=yn>.
设zkxm
，则可加xm=yn
到Z，得到一个长为k+1的
X与Y的公共序列，与Z是X和Y的LCS矛盾。于是
zk=xm=yn
。
现在证明Zk-1
是Xm-1
与Yn-1
的LCS。显然Zk-1
是Xm-
1
与Yn-1
的公共序列。我们需要证明Zk-1
是LCS。
设不然，则存在Xm-1
与Yn-1
的公共子序列W，W
的长大于k-1。增加xm=yn
到W，我们得到一个长
大于k的X与Y的公共序列，与Z是LCS矛盾。于
是，Zk-1
是Xm-1
与Yn-1
的LCS.
⑵ X=<x1, …, xm-1, xm>, Y=<y1, …, yn-1, yn>，
xmyn
，zkxm
，则 LCSXY= LCSXm-1Y
由于zkxm
，Z是Xm-1
与Y的公共子序列。我
们来证Z是Xm-1
与Y的LCS。设Xm-1
与Y有一
个公共子序列W，W的长大于k, 则W也是X
与Y 的公共子序列，与Z是LCS矛盾。
⑶ 同⑵可证。
X和Y的LCS的优化解结构为
LCSXY=LCSXm-1Yn-1
+ <xm=yn> if xm=yn
LCSXY=LCSXm-1Y if xm≠yn, zk≠xm
LCSXY=LCSXYn-1 if xm≠yn, zk≠yn

建立LCS长度的递归方程
• C[i, j] = Xi与Yj 的LCS的长度
• LCS长度的递归方程
C[i, j] = 0 if i=0 或 j=0
C[i, j] = C[i-1, j-1] + 1 if i, j>0 且 xi = yj
C[i, j] = Max(C[i, j-1], C[i-1, j]) if i, j>0 且 xi ≠ yj
 
自底向上计算LCS的长度

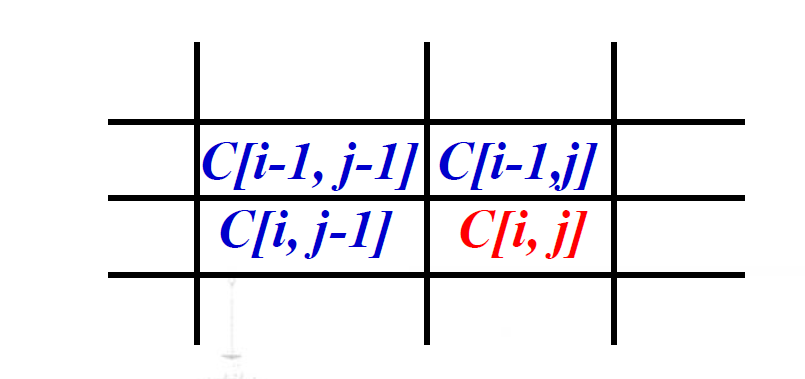
计算LCS长度的算法
– 数据结构
C[0:m,0:n]: C[i,j]是Xi
与Yj
的LCS的长度
B[1:m,1:n]: B[i,j] 是指针， 指向计算
C[i,j]时所选择的子问题的优化解所对
应的C表的表项
 
LCS-length(X, Y)
m←length(X)；n←length(Y)；
For i←1 To m Do C[i,0]←0;
For j←1 To n Do C[0,j]←0;
For i←1 To m Do
For j←1 To n Do
If xi = yj
Then C[i,j]←C[i-1,j-1]+1；B[i,j]←“↖”;
Else If C[i-1,j]≥C[i,j-1]
Then C[i,j]≥C[i-1,j]; B[i,j]←“↑”;
Else C[i,j]≥C[i,j-1]; B[i,j]←“←”;
Return C and B.
构造优化解
• 基本思想
– 从B[m, n]开始按指针搜索
– 若B[i, j]=“↖”，则xi=yj
是LCS的一个元
素
– 如此找到的“LCS”是X与Y的LCS
Print-LCS(B, X, i, j)
IF i=0 or j=0 THEN Return;
IF B[i, j]=“↖”
THEN Print-LCS(B, X, i-1, j-1);
Print xi;
ELSE If B[i, j]=“↑”
THEN Print-LCS(B, X, i-1, j);
ELSE Print-LCS(B, X, i, j-1).
 
Print-LCS(B, X, length(X), length(Y))
可打印出X与Y的LCS。

      /*功能：计算最优值
       *参数：
       *        x:字符串x  X:字符串x最大长度
       *        y:字符串y   Y:字符串y最大长度
       *        b:标志数组
       *        xlen:字符串x的长度
       *        ylen:字符串y的长度
       *返回值：最长公共子序列的长度
       *
       */
      int Lcs_Length(string x, string y, int b[][Y+],int xlen,int ylen)
      {
          int i = ;
          int j = ;
 
          int c[X+][Y+];
          for (i = ; i<=xlen; i++)
          {
              c[i][]=;
          }
          for (i = ; i <= ylen; i++ )
          {
              c[][i]=;
          }
          for (i = ; i <= xlen; i++)
          {
 
              for (j = ; j <= ylen; j++)
              {
                  if (x[i - ] == y[j - ])
                  {
                      c[i][j] = c[i-][j-]+;
                      b[i][j] = ;
                  }
                  else
                      if (c[i-][j] > c[i][j-])
                      {
                          c[i][j] = c[i-][j];
                          b[i][j] = ;
                      }
                      else
                          if(c[i-][j] <= c[i][j-])
                          {
                              c[i][j] = c[i][j-];
                              b[i][j] = ;
                          }
 
              }
          }
 
          cout << "计算最优值效果图如下所示：" << endl;
          for(i = ; i <= xlen; i++)
          {
              for(j = ; j < ylen; j++)
              {
                  cout << c[i][j] << " ";
              }
              cout << endl;
          }
 
          return c[xlen][ylen];
      }

完整代码

    //只能打印一个最长公共子序列
    #include <iostream>
    using namespace std;
 
     const int X = 1000, Y = 1000;        //串的最大长度
     char result[X+1];                    //用于保存结果
     int count=0;                        //用于保存公共最长公共子串的个数
 	 int c[X+1][Y+1];
 	 int b[X + 1][Y + 1];
     /*功能：计算最优值
      *参数：
      *        x:字符串x
      *        y:字符串y
      *        b:标志数组
      *        xlen:字符串x的长度
      *        ylen:字符串y的长度
      *返回值：最长公共子序列的长度
      *
      */
     int Lcs_Length(string x, string y, int b[][Y+1],int xlen,int ylen)
     {
         int i = 0;
         int j = 0;
 
         //int c[X+1][Y+1];
         for (i = 0; i<=xlen; i++)
         {
             c[i][0]=0;
         }
         for (i = 0; i <= ylen; i++ )
         {
             c[0][i]=0;
         }
         for (i = 1; i <= xlen; i++)
         {
 
             for (j = 1; j <= ylen; j++)
             {
                 if (x[i - 1] == y[j - 1])
                 {
                     c[i][j] = c[i-1][j-1]+1;
                     b[i][j] = 1;
                 }
                 else
                     if (c[i-1][j] > c[i][j-1])
                     {
                         c[i][j] = c[i-1][j];
                         b[i][j] = 2;
                     }
                     else
                         if(c[i-1][j] <= c[i][j-1])
                         {
                             c[i][j] = c[i][j-1];
                             b[i][j] = 3;
                         }
 
             }
         }
         /*
         cout << "计算最优值效果图如下所示：" << endl;
         for(i = 1; i <= xlen; i++)
         {
             for(j = 1; j < ylen; j++)
             {
                 cout << c[i][j] << " ";
             }
             cout << endl;
         }
         */
         return c[xlen][ylen];
     }
 
    void Display_Lcs(int i, int j, string x, int b[][Y+1],int current_Len)
     {
         if (i ==0 || j==0)
         {
             return;
         }
         if(b[i][j]== 1)
         {
             current_Len--;
             result[current_Len]=x[i- 1];
             Display_Lcs(i-1, j-1, x, b, current_Len);
         }
         else
         {
             if(b[i][j] == 2)
             {
                 Display_Lcs(i-1, j, x, b, current_Len);
             }
             else
             {
                 if(b[i][j]==3)
                 {
                     Display_Lcs(i, j-1, x, b, current_Len);
                 }
                 else
                 {
                     Display_Lcs(i-1,j,x,b, current_Len);
                 }
             }
         }
     }
 
     int main(int argc, char* argv[])
     {
         string x;
         string y;
         cin>>x>>y;
         int xlen = x.length();
         int ylen = y.length();
 
         //int b[X + 1][Y + 1];
 
         int lcs_max_len = Lcs_Length( x, y, b, xlen,ylen );
         //cout << lcs_max_len << endl;
 
         Display_Lcs( xlen, ylen, x, b, lcs_max_len );
 
         //打印结果如下所示
        for(int i = 0; i < lcs_max_len; i++)
        {
            cout << result[i];
        }
        cout << endl;
         return 0;
     }

算法复杂性：

• 时间复杂性
– 计算代价的时间
• (i, j)两层循环,i循环m步, j循环n步
• O(mn)
– 构造最优解的时间: O(m+n)
– 总时间复杂性为：O(mn)
• 空降复杂性
– 使用数组C和B
– 需要空间O(mn)