[九省联考2018] 一双木棋 chess

Description

菲菲和牛牛在一块n 行m 列的棋盘上下棋，菲菲执黑棋先手，牛牛执白棋后手。 棋局开始时，棋盘上没有任何棋子，两人轮流在格子上落子，直到填满棋盘时结束。

落子的规则是：一个格子可以落子当且仅当这个格子内没有棋子且这个格子的左侧及上方的所有格子内都有棋子。

棋盘的每个格子上，都写有两个非负整数，从上到下第i 行中从左到右第j 列的格 子上的两个整数记作A_i,j,，B_i,j 。在游戏结束后，菲菲和牛牛会分别计算自己的得分：菲菲的得分是所有有黑棋的格子上的A_i,j​ 之和，牛牛的得分是所有有白棋的格子上的B_i,j 的和。

菲菲和牛牛都希望，自己的得分减去对方的得分得到的结果最大。现在他们想知道，在给定的棋盘上，如果双方都采用最优策略且知道对方会采用最优策略，那么，最终的结果如何。

Input

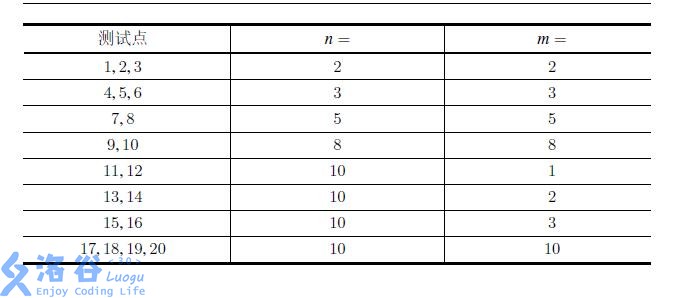
输入第一行包含两个正整数n;m，保证n;m <= 10。

接下来n 行，每行m 个非负整数，按从上到下从左到右的顺序描述每个格子上的 第一个非负整数：其中第i 行中第j 个数表示A_i,j 。

接下来n 行，每行m 个非负整数，按从上到下从左到右的顺序描述每个格子上的 第二个非负整数：其中第i 行中第j 个数表示B_i,j​ 。

Output

输出一个整数，表示菲菲的得分减去牛牛的得分的结果。

对于所有的测试数据，n;m <= 10 ，A_i,j; B_i,j​ <= 100000。

对于编号为奇数的测试点，保证所有的B_i,j​ = 0 。

Solution

考场上没想出来写的 30 分暴力诶

没想到现在就已经会了

我们定义某一时刻棋盘上的落子情况为当前的状态

定义 s 为初状态，即棋盘上还没有落子

定义 t 为末状态，即棋盘上已经落完子

不难证明，合法的状态小于二十万种

那么先 HASH 一下每个状态，令其唯一对应一个正整数

对于每一个状态，我们可以知道它是从哪些状态转移来的

定义 num[i] 表示 i 状态落了多少子，方便判断当前是该先手还是该后手。

我们 dp 要倒着推，因为如果正着推，有可能出现当前虽然求出了最大价值，但是却不是他们的最优策略的情况。

所以定义 f[i] 表示从状态 i 到末状态 t 先手减后手的最大价值

f[t] 初值为0，f[1] 即为答案

但是怎么求中间状态 f[i] 的值呢？

之前提到过，可以求出 i 状态是由 哪些状态转移来的，假设有一个状态为 j 可以转移到 i

我们用 num 数组求出在状态 j 时是先手下了还是后手下了最后一个棋子，然后分情况讨论

如果是先手：考虑后手的最优策略，显然是想让 f[i] 最小，所以 f[i]=min{f[j]-b[x][y]}，x、y 是 j 转移到 i 状态落子的横纵坐标

同理，如果为后手：那么 f[i] 最大的转移方程是 f[i]=max{f[j]+a[x][y]}，x、y 的意义跟上面一样

那我们现在就剩最后一个问题了：怎么进行转移呢？

我这里利用了拓扑序进行转移：如果一个状态被所有的后续状态遍历完并求出最优解后，就将其 push 进队列里，让它去转移别人即可。

最坏情况时间复杂度 $O(18万*180万)$ 但是开氧气优化跑的贼快，最慢的点 300ms (反正省选也开 O2 不算作弊)

Code

// By YoungNeal
#include<map>
#include<queue>
#include<cstdio>
#include<cctype>
#define N 400005
#define int long long
#define mod 1000000007
using namespace std;

int head[N];
int cnt,s,t;
int n,m,tot;
int qp[N][];
int f[N],fz[];
int deg[N],num[N];
int a[][],b[][];

map<int,int> mp;
queue<int> topo;

struct Edge{
    int to,nxt,disa,disb;
}edge[N*];

void add(int x,int y,int z,int p){
    edge[++cnt].to=y;
    edge[cnt].nxt=head[x];
    edge[cnt].disa=z;
    edge[cnt].disb=p;
    head[x]=cnt;
}

void hsh(int x){
    int d=;tot++;
    for(int i=;i<=n;i++)
        d=d*+fz[i],d%=mod,qp[tot][i]=fz[i];
    mp[d]=tot;
    num[tot]=x;
    if(num[tot]&) f[tot]=2e18;
    else f[tot]=-2e18;
}

void dfs(int now,int lim,int num){
    if(now>n){
        hsh(num);
        return;
    }
    for(int i=;i<=lim;i++)
        fz[now]=i,dfs(now+,i,num+i);
}

void _find(){
    int x=,y=;
    for(int i=;i<=n;i++) y=y*+m,y%=mod;
    s=mp[x],t=mp[y];
}

void read(int &x){
    x=;char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) x=(x<<)+(x<<)+(ch^),ch=getchar();
}

signed main(){
    scanf("%lld%lld",&n,&m);
    for(int i=;i<=n;i++){
        for(int j=;j<=m;j++) read(a[i][j]);
    }
    for(int i=;i<=n;i++){
        for(int j=;j<=m;j++) read(b[i][j]);
    }
    dfs(,m,);
    _find();
    f[t]=;
    for(int i=;i<=tot;i++){
        for(int j=n;j;j--){
            if(qp[i][j]==qp[i][j+]) continue;
            int x=;int idx=j,idy=qp[i][j];
            for(int p=;p<=n;p++){
                if(p==j) x=x*+qp[i][j]-,x%=mod;
                else x=x*+qp[i][p],x%=mod;
            }
            if(num[i]&) add(i,mp[x],a[idx][idy],);
            else add(i,mp[x],,b[idx][idy]);
            deg[mp[x]]++;
        }
    }
    topo.push(t);
    while(topo.size()){
        int u=topo.front();topo.pop();
        for(int i=head[u];i;i=edge[i].nxt){
            int to=edge[i].to;
            if(num[to]&) f[to]=min(f[to],f[u]-edge[i].disb);
            else f[to]=max(f[to],f[u]+edge[i].disa);
            deg[to]--;
            if(!deg[to]) topo.push(to);
        }
    }
    printf("%lld\n",f[]);
    return ;
}