谈谈我对Manacher算法的理解

Manacher算法其实是求字符串里面最长的回文。

①在学习该算法前，我们应该知道回文的定义：顺序读取回文和逆序读取回文得到的结果是一样的，如：abba，aba。

那么我们不难想到，在判断一个字符串str是否为回文之前，需要判断str中字符的个数的奇偶性。

②为了简化这一个冗杂的判断过程，Manacher算法对字符串str进行了预处理：

在每个字符之间插入一个一定不会出现的字符，如 ‘#’，'$'等。

为了后面我们更好地对字符串进行操作，我们可以在开头加一个标识符，标识字符串的开头（这里以'$'为例）。

到了这一步，无论原来字符串奇偶如何，现在都变成了偶数字符串。

③做完预处理之后，下一步就是求取 p[ ] 数组（随便取什么名字都可以）

p[ i ]数组的含义是存放以 s[ i ]为中心，最长回文的单边长度。我们来看一下下面的图来更好地理解：

以s[ 4 ] == 2为例，s[ 4 ]左右各移动一位 → 得到字符：# 和 # 相等；s[ 4 ]左右各移动两位 → 得到字符：1 和 2 不相等；

停止移动，因此p[ 4 ]位置该存放 2，以s[ 4 ]为中心最长回文的单边长度（包含s[ 4 ] ）。

得到 p[ ] 数组之后我们就可以很简单地知道字符串str中的最长回文长度及最长回文了。

④ p[ ] 数组求取过程的技巧：

思考：在已经知道p [ 0 ] ~ p [ id ] 的情况下如何快速求取  p[ i ] 呢？

我们来看看下面这张图：以 s [ id ] 为中心的最长回文能够管辖的区域是s [ my ] ~ s [ mx ]

而 i 是落在了 my ~ mx 中。由于对称性，能够找到 j 使 s [ i ] == s [ j ] 同时 p [ i ] == p [ j ]

那么这个时候，可以直接令p [ i ] = p [ j ]。

同样地，在 id~mx 这个范围中的p [ ] 都能通过对称求出来。

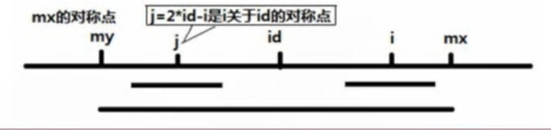
如果 i 落在mx右边的话，前半部分可以用对称，后半部分只能暴力求 p [  ]啦~

---

以上只是自己的一些拙见，如果有不正确的地方，欢迎指出。