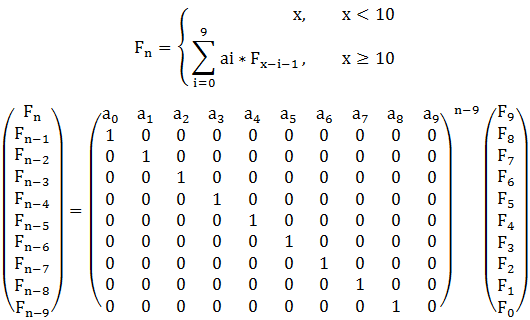hdu 1757 A Simple Math Problem (矩阵快速幂)
Description
If x < 10 f(x) = x.
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
And ai(0<=i<=9) can only be 0 or 1 .
Now, I will give a0 ~ a9 and two positive integers k and m ,and could you help Lele to caculate f(k)%m.
Input
In each case, there will be two lines.
In the first line , there are two positive integers k and m. ( k<2*10^9 , m < 10^5 )
In the second line , there are ten integers represent a0 ~ a9.
Output
Sample Input
10 9999
1 1 1 1 1 1 1 1 1 1
20 500
1 0 1 0 1 0 1 0 1 0
Sample Output
45
104 这就算我写的第一道矩阵快速幂的题了!
矩阵快速幂的给我的感觉就是先找规律,YY出一个n*n的矩阵,矩阵左边写一列数,矩阵右边写一列数。让矩阵乘上右边那一列数等于左边的那列数。盗张图!!
然后......然后就没有然后了QWQ,输出答案就行了。
代码如下:
#include <bits/stdc++.h> using namespace std;
const int N=;
int k,m;
struct Matrix//用结构体来存矩阵
{
long long int mat[N][N];//直接上long long int 别找事
}matrix;
void init()
{
for (int i=;i<N;++i)
scanf("%lld",&matrix.mat[][i]);
for (int i=;i<N;++i)
{
for (int j=;j<N;++j)
{
if (i==j+)
matrix.mat[i][j]=;
else
matrix.mat[i][j]=;
}
}
}
Matrix operator * (Matrix a,Matrix b)//定义乘号
{
Matrix c;
for (int i=;i<N;++i)
{
for (int j=;j<N;++j)
{
c.mat[i][j]=;//初始化值为0
for (int k=;k<N;++k)
c.mat[i][j]+=a.mat[i][k]*b.mat[k][j];
c.mat[i][j]%=m;//记得取模,否则就炸了
}
}
return c;
}
Matrix Pow (int n)//定义快速幂函数
{
Matrix t;
if (n==)
return matrix;
if (n&)
return matrix*Pow(n-);
else
{
Matrix temp=Pow(n>>);
return temp*temp;
}
}
int main()
{
//freopen("de.txt","r",stdin);
while (~scanf("%d%d",&k,&m))
{
init();
if (k<)
{
printf("%lld\n",matrix.mat[][k]%m);
continue;
}
Matrix temp=Pow(k-);
long long int ans=;
for (int i=;i<N;++i)
{
ans += temp.mat[][i]*(N-i-);
ans%=m;
}
printf("%lld\n",ans);
}
return ;
}
hdu 1757 A Simple Math Problem (矩阵快速幂)的更多相关文章
- HDU 1757 A Simple Math Problem (矩阵快速幂)
题目 A Simple Math Problem 解析 矩阵快速幂模板题 构造矩阵 \[\begin{bmatrix}a_0&a_1&a_2&a_3&a_4&a ...
- hdu 1757 A Simple Math Problem_矩阵快速幂
题意:略 简单的矩阵快速幂就行了 #include <iostream> #include <cstdio> #include <cstring> using na ...
- HDU 1757 A Simple Math Problem(矩阵)
A Simple Math Problem [题目链接]A Simple Math Problem [题目类型]矩阵快速幂 &题解: 这是一个模板题,也算是入门了吧. 推荐一个博客:点这里 跟 ...
- HDU1757 A Simple Math Problem 矩阵快速幂
A Simple Math Problem Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Ot ...
- A Simple Math Problem(矩阵快速幂)----------------------蓝桥备战系列
Lele now is thinking about a simple function f(x). If x < 10 f(x) = x. If x >= 10 f(x) = a0 ...
- HDU 1757 A Simple Math Problem 【矩阵经典7 构造矩阵递推式】
任意门:http://acm.hdu.edu.cn/showproblem.php?pid=1757 A Simple Math Problem Time Limit: 3000/1000 MS (J ...
- HDU 1757 A Simple Math Problem(矩阵快速幂)
题目链接 题意 :给你m和k, 让你求f(k)%m.如果k<10,f(k) = k,否则 f(k) = a0 * f(k-1) + a1 * f(k-2) + a2 * f(k-3) + …… ...
- hdu 1757 A Simple Math Problem (矩阵快速幂,简单)
题目 也是和LightOJ 1096 和LightOJ 1065 差不多的简单题目. #include<stdio.h> #include<string.h> #include ...
- HDU 1757 A Simple Math Problem( 矩阵快速幂 )
<font color = red , size = '4'>下列图表转载自 efreet 链接:传送门 题意:给出递推关系,求 f(k) % m 的值, 思路: 因为 k<2 * ...
随机推荐
- 在python3.7下怎么安装matplotlib与numpy
一.安装matplotlib 1.在Matplotlib的官网下载电脑对应的版本,网址为:https://pypi.org/project/matplotlib/#files 2.将在下载的.whl文 ...
- JAVA中STL使用
Vector:和c++的vector使用方法类似. Vector<Integer> vec=new Vector<> (); ArrayList:Java.util.Array ...
- 嵌入式开发环境搭建(一) 虚拟机实现桥接Ethernet网口 并且通过WIFI进行NAT联网
背景: 目前手头上有一块JZ2440的板子,之前有搭建完整套开发环境,由于虚拟机故障需要从新搭建服务器端,故在此记录搭建步骤 环境: Ubuntu16.4 VMWare 12 先行条件: 先按照自定义 ...
- xml解析用正则解决没有标签的文本的解析不出异常
如 <q>sasas<w>eqwe</w>ddas</q> package com.people.xmlToSql; import java.io.F ...
- ActiveReports报表数据源:运行时数据源
ActiveReports 支持在设计时和运行时设置报表数据源,本文将重点介绍如何在运行时为区域报表和RDL/页面报表设置报表数据源. ·第一步: 在工程中创建一个名为 SectionReport_D ...
- appium常见问题02_android内嵌H5页(webview)如何定位
现在大多数app都是由原生页面和内嵌H5(即webview)组成,app原生页面直接定位即可,那内嵌H5页面要如何定位呢. 相信大多数人用appium做自动化时都有遇到这个问题,小编总结了下工作中该问 ...
- 从0开始的InfiniBand硬件踩坑过程
由于科学计算实验的需求,需要使用InfiniBand做一个持久性内存全互联的分布式存储系统.其中从网卡到交换机使用Mellanox全家桶,而在Mellanox网卡与交换机的使用过程中还是遇到了不少的问 ...
- C++中的静态成员函数
1,问完成的需求: 1,统计在程序运行期间某个类的对象数目: 1,静态成员变量满足了这个需求: 2,保证程序的安全性(不能使用全局变量): 3,随时可以获取当前对象的数目: 1,有没有什么特别的地方或 ...
- JS高级程序随笔一
function Aarguments(x,y){ for(var i=0;i<arguments.length;i++){ alert(arguments[i]); }; }; Aargume ...
- UVA 10256 The Great Divide(凸包划分)
The Great Divide Input: standard input Output: standard output Time Limit: 8 seconds Memory Limit: 3 ...