校内题目T2695 桶哥的问题——吃桶

同T2一样外校蒟蒻可能没看过：

题目描述：

题目背景

@桶哥

桶哥的桶没有送完。

题目描述

桶哥的桶没有送完，他还有n个桶。他决定把这些桶吃掉。他的每一个桶两个属性：种类aia_iai​和美味值bib_ibi​。若下标为x, y, z（下标从1开始）的三个桶满足:

x<z x < z x<z 且 x+y=z−2y x + y = z - 2y x+y=z−2y 且 ax=az a_x = a_z ax​=az​

那么它们构成一个套餐，会产生

(x+z)∗(bx−bz) (x + z) * (b_x - b_z) (x+z)∗(bx​−bz​)

的价值。问：一共会产生多少价值？

上面那个看不清楚的下标是z

输入输出格式

输入格式：

第一行两个整数n,mn,mn,m，表示共有m种共n个桶。

第二行n个整数表示bib_ibi​,

第三行n个整数表示aia_iai​,（下标）

输出格式：

一行一个整数，表示一共会产生多少价值。由于这个数可能很大，你只需要输出它除以10007的余数。

如果答案是负的，请将其加上10007再对10007取余。如-1应输出10006.

---

正解开始：

然而_rqy大佬讲的我并没怎么听懂，所以也是一蒙一蒙的。

转换一下公式：

x+y=z-2y
z-x=3y
x,z种类相等

那么把求价值公式：

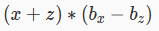
展开得：xbx+zbx-xbz-zbz(注意下标)，

也就是说，这个东西和y半毛钱关系都没有！

理一下关系：

1,z>x

2.z-x为3的倍数

3.z和x为同一种类的桶

那么考虑思路：同余枚举

一个数%3无非是余1余2余3（余0）

那么从1,2,3开始，按下标网上枚举，分3种，分别对应3个不同外循环，而内循环就是网上枚举到最后一个下标，那么别看是双重循环，但是你把枚举次数加起来，是O(n)的。

直接快了好多QWQ

那么回归正题：

内层循环干什么？

当然是利用∑来求和了

安利核心公式：

（x+z）*（b_x-b_z）=∑x*b_x+z*∑b_x-b_z*∑x-z*b_z*∑1

为什么∑的地方不同呢？？？

因为我们要对z枚举（或者x也行），这样把上一层求和的就给保存下来继续用而不是再for循环求一遍

其实用双层循环而不是三重循环来求阶乘也是一个道理

因为z<x,也就是说对于每一个z，前面从0到z-3的x都满足，都要被加进∑内部

每次只加一个而不是又来一遍for循环。。。

这个比较清楚了吧。。。。。。

上代码了。。。QWQ

#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>

int readInt() {//快读
  int ans = , c, f = ;
  while (!isdigit(c = getchar()))
    if (c == '-') f *= -;
  do ans = ans *  + c - '';
  while (isdigit(c = getchar()));
  return ans * f;
}

const int mod = ;//定义%数组 

int b[], a[];
int S[], Sx[], Sbx[], Sxbx[];//s为∑

int main() {
  int n = readInt(); /* m = */readInt();
  for(int i = ; i <= n; i++) b[i] = readInt() % mod;
  for(int i = ; i <= n; i++) a[i] = readInt();
  int ans = ;
  for (int cc = ; cc <= ; ++cc) {
    // { cc, cc+3, cc+6 ... } 分一组
    memset(S, , sizeof(S));
    memset(Sx, , sizeof(Sx));
    memset(Sbx, , sizeof(Sbx));
    memset(Sxbx, , sizeof(Sxbx));
    for(int i = cc; i <= n; i += ) {
      ans = (ans + i % mod * Sbx[a[i]] % mod) % mod;
      ans = (ans - b[i] * Sx[a[i]] % mod) % mod;
      ans = (ans + Sxbx[a[i]]) % mod;
      ans = (ans - S[a[i]] * b[i] % mod * (i % mod) % mod) % mod;
      S[a[i]] = (S[a[i]] + ) % mod;
      Sx[a[i]] = (Sx[a[i]] + i) % mod;
      Sbx[a[i]] = (Sbx[a[i]] + b[i]) % mod;
      Sxbx[a[i]] = (Sxbx[a[i]] + i % mod * b[i] % mod) % mod;
    }
  }
  printf("%d", (ans + mod) % mod);
  return ;
}

气喘吁吁的甩胳膊，，

%_rqy大佬，是他出的题和给我们讲的题！