HDU 6206 Apple ( 高精度 && 计算几何 && 三点构圆求圆心半径 )

题意 : 给出四个点，问你第四个点是否在前三个点构成的圆内，若在圆外输出"Accepted"，否则输出"Rejected"，题目保证前三个点不在一条直线上。

分析 : 简单的计算几何问题，如果能够知道圆心和半径(Radius)以及第四个点和圆心的距离(Distance)，我们就能够判断第四个点是否在圆外，例如Distance > Radius则在圆外。三点构圆 的圆心和半径是能够推导出公式的

（参考==> http://blog.csdn.net/death10001/article/details/77389128 ）

设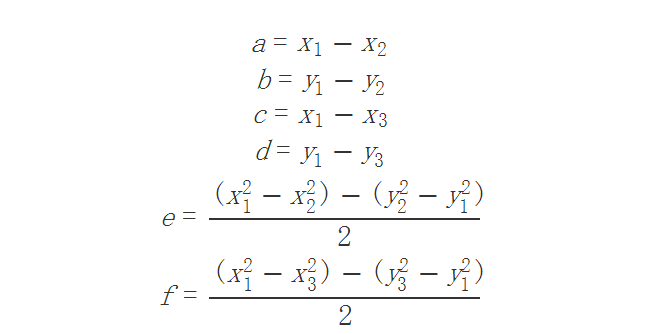 

则有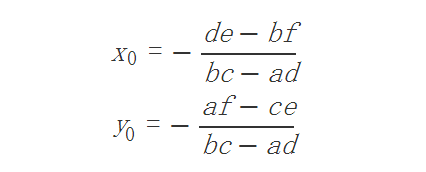

根据两点间距离公式可得半径平方R² = (X - X₀)² + (Y - Y₀)² 我们将刚刚的X₀代数式和X(三个点的任何一个)代进去通分一下就能得到

[ 2*X*(bc-ad)+(de-bf) / 2(bc-ad) ]² + [ 2*Y*(bc-ad)+(af-ce) / 2(bc-ad) ]² 

发现分母都是一样，可以通分。然后呢，还是根据两点间距我们可以用同样的方法得到第四个点和圆心之间的距离的平方并且分母同样是2(bc-ad)，所以运算的过程当中就避免了进行影响精度的除法运算，比较R和Dis只要比较两个分子即可，高精度用BigInteger解决。

import java.util.Scanner;
import java.util.*;
import java.math.*;
import java.io.*;
class PO{ BigInteger x, y; }
public class Main{
    public static boolean Solve(PO p1, PO p2, PO p3, PO p){
        //-------------------------------------------------------------------------------------

        BigInteger a = p1.x.subtract(p2.x);
        BigInteger b = p1.y.subtract(p2.y);
        BigInteger c = p1.x.subtract(p3.x);
        BigInteger d = p1.y.subtract(p3.y);
        BigInteger e = (((p1.x).multiply(p1.x)).subtract((p2.x).multiply(p2.x))).subtract(((p2.y).multiply(p2.y)).subtract(((p1.y).multiply(p1.y))));
        BigInteger f = (((p1.x).multiply(p1.x)).subtract((p3.x).multiply(p3.x))).subtract(((p3.y).multiply(p3.y)).subtract(((p1.y).multiply(p1.y))));
        BigInteger two = new BigInteger("2");

        //-------------------------------------------------------------------------------------

        BigInteger tmp1 = (((p1.x).multiply((b.multiply(c)).subtract((a.multiply(d))))).multiply(two)).add((d.multiply(e)).subtract((b.multiply(f))));
        tmp1 = tmp1.multiply(tmp1);
        BigInteger tmp2 = (((p1.y).multiply((b.multiply(c)).subtract((a.multiply(d))))).multiply(two)).add((a.multiply(f)).subtract((c.multiply(e))));
        tmp2 = tmp2.multiply(tmp2);
        BigInteger R = tmp1.add(tmp2);///计算出半径的"长度" ( 实际是代数式的分子 )

        //-------------------------------------------------------------------------------------

        tmp1 = (((p.x).multiply((b.multiply(c)).subtract((a.multiply(d))))).multiply(two)).add((d.multiply(e)).subtract((b.multiply(f))));
        tmp1 = tmp1.multiply(tmp1);
        tmp2 = (((p.y).multiply((b.multiply(c)).subtract((a.multiply(d))))).multiply(two)).add((a.multiply(f)).subtract((c.multiply(e))));
        tmp2 = tmp2.multiply(tmp2);
        BigInteger Dis = tmp1.add(tmp2);///计算出圆心到第四个点的"距离"

        if(R.compareTo(Dis) < 0) return true;
        else return false;
    }
    public static void main (String[] args) throws Exception{
        Scanner cin = new Scanner(new BufferedInputStream(System.in));
        int nCase = cin.nextInt();
        for(int t=1; t<=nCase; t++){
            PO p1 = new PO(); PO p2 = new PO();
            PO p3 = new PO(); PO aim= new PO();
            p1.x = cin.nextBigInteger(); p1.y = cin.nextBigInteger();
            p2.x = cin.nextBigInteger(); p2.y = cin.nextBigInteger();
            p3.x = cin.nextBigInteger(); p3.y = cin.nextBigInteger();
            aim.x = cin.nextBigInteger(); aim.y = cin.nextBigInteger();
            boolean res = Solve(p1, p2, p3, aim);
            if(res) System.out.println("Accepted");
            else System.out.println("Rejected");
        }
    }
}

瞎 : 实际上还有更简便的方法，直接能用更直接的公式算出圆心 (x0, y0) 和半径的平方 r^2

x0=((y2-y1)*(y3*y3-y1*y1+x3*x3-x1*x1)-(y3-y1)*(y2*y2-y1*y1+x2*x2-x1*x1))/(2.0*((x3-x1)*(y2-y1)-(x2-x1)*(y3-y1)));

y0=((x2-x1)*(x3*x3-x1*x1+y3*y3-y1*y1)-(x3-x1)*(x2*x2-x1*x1+y2*y2-y1*y1))/(2.0*((y3-y1)*(x2-x1)-(y2-y1)*(x3-x1)));

r^2=(x1-x0)*(x1-x0)+(y1-y0)*(y1-y0);

里面涉及除法，那就用BigDecimal就能解决了，参考 ==> http://blog.csdn.net/cillyb/article/details/78012069