class-逻辑回归与最大熵模型

我们知道，线性回归能够进行简单的分类，但是它有一个问题是分类的范围问题，只有加上一个逻辑函数，才能使得其概率值位于0到1之间，因此本次介绍逻辑回归问题。同时，最大熵模型也是对数线性模型，在介绍最大熵模型的同时需要了解拉格朗日对偶法对约束最优化问题的求解，在文章末有几个关于牛顿法的链接，可供拓展阅读。

 

内容：

1 logistic regression model
1.1 logistic distribution
1.2 binary logistic regression model
1.3 模型参数估计
1.4 multi-nominal logistic regression model
2 最大熵模型
2.1 最大熵原理
2.2 最大熵模型定义
2.3 最大熵模型的学习training
2.4 极大似然估计
3 模型训练算法
3.1 改进迭代尺度法(IIS)
3.2 拟牛顿法

logistic regression和maximum entropy model 都属于对数线性模型。

1 logistic regression model

1.1 logistic distribution

定义：设X是连续分布随机变量，X服从logistic distribution是指具有下列分布函数和密度函数：



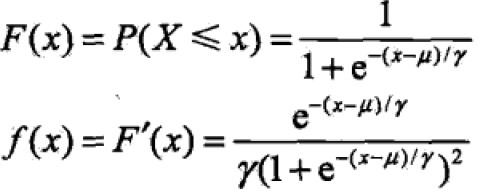
where，μ为位置参数，γ>0为形状参数。

分布曲线：



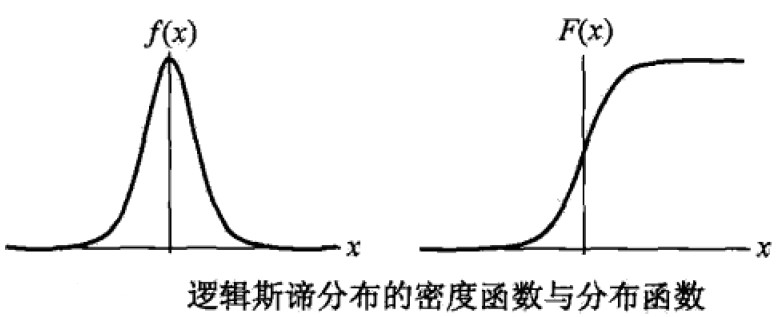
F(x)为S型曲线（sigmoid curve），以(μ，1/2)中心对称，即：，γ越小中间位置增长越快。

1.2 binary logistic regression model

二项逻辑回归模型是一种分类模型，用条件概率P(Y|X)表示,X取值为实数，Y取值为0或1。通过监督学习来估计模型参数。

条件概率分布：



where，x属于Rn是输入，Y属于{0,1}，w是权值向量，b是偏置，w·x是内积inner product。

逻辑回归是对于给定的输入实例x求得P(Y=1|x)和P(Y=0|x)的概率，取概率较大者的类别作为x的分类。

为了简化将w,x扩充为w=(w1,w2,…,wn,b),x=(x1,x2,…,xn,1),则logistic distribution为：



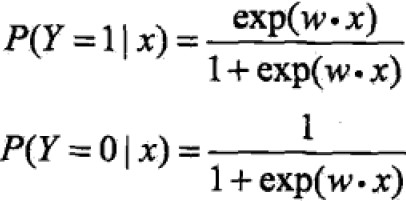
一个事件的几率odds是指该事件发生的概率与不发生的概率比值，若发生为p，则几率为p/(1-p),该事件的对数几率log odds为：。

代入上式可得：

说明：输出Y=1的对数几率是输入x的线性函数，对输入x分类的线性函数w·x其值域为实数域，线性函数的值越接近于无穷，概率值就越接近于1，线性函数的值越接近负无穷概率值就越接近于0，这就是逻辑回归model。

1.3 模型参数估计

这样，目标函数变为对数似然函数为目标函数的最优化问题，常用gradient descent 或者拟牛顿法求解，那么学到的model是：w hat是w的最大似然估计值

似然函数的理解1

wiki百科

似然函数就是likelihood function，似然也是一种概率，但是是对已知结果对参数预测进行估计。更大的作用在于当参数变化时似然性的改变，变大就更有“说服力”。

1.4 multi-nominal logistic regression model

与1.2的区别就是Y取值为{1,2,3,…,K},参数估计法也是类似的。



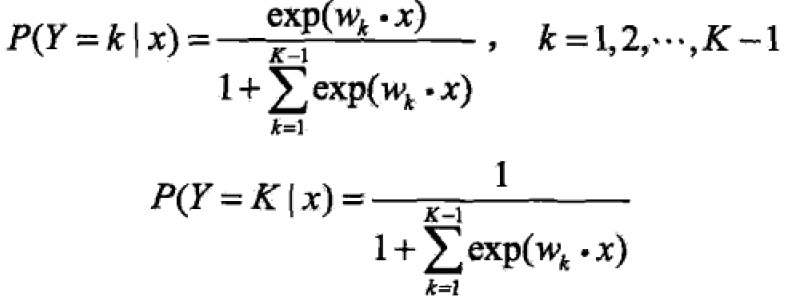
推荐阅读：http://blog.jobbole.com/88521/

https://www.cnblogs.com/sparkwen/p/3441197.html

2 最大熵模型

2.1 最大熵原理

最大熵原理经过推导将得到最大熵模型，其实它是一个概率模型的学习准则。最大熵原理认为学习概率模型时，在所有可能model中，熵最大的model是最好的model，若有约束条件，则是在此条件下选取熵最大的model。

假设离散随机变量X的概率分布为P(X),其熵为：，满足。

where，|X|是X的取值个数，当且仅当 X满足均匀分布时等号成立，即均匀分布熵最大。

首先要满足已有事实即约束条件，如果没有别的条件时（如果仅有概率和为1）不确定信息就通过熵的最大化来表示等可能（均匀分布，等可能概率）。

2.2 最大熵模型定义

目标是利用最大熵原理选择最好的分类模型。

考虑模型应该满足的条件：训练集T={{(x1,y1),…(xN,yN)}};可以确定联合概率分布P(X=x,Y=y),边缘概率分布P(X=x):

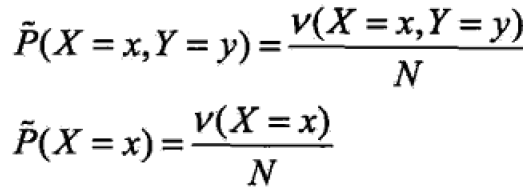ν是出现的频次，N是总样本数（通过频率来表示概率）

特征函数(feature function)：f(x,y)描述输入x与输出y之间的某一事实。定义为：



特征函数与经验分布的期望值：；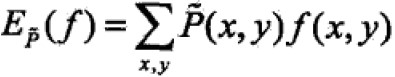

进而特征函数关于模型P(Y|X)与经验分布的P(X=x)期望值：；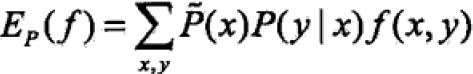

注：若model能够获取训练数据的信息，那么可以假设这两个期望值相等——这就是model学习的约束条件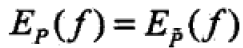，其中有n个特征函数就有n个约束条件。

最大熵模型：假设所有满足约束条件的模型集合：



定义在条件概率分布P(Y|X)上的条件熵为：



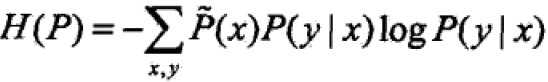
其中，集合C中条件熵H(P)最大的模型称为最大熵模型，对数为自然对数。

2.3 最大熵模型的学习training

最大熵模型的学习就是求解最大熵模型的过程，即约束条件下找最优化的问题（约束最优化）。

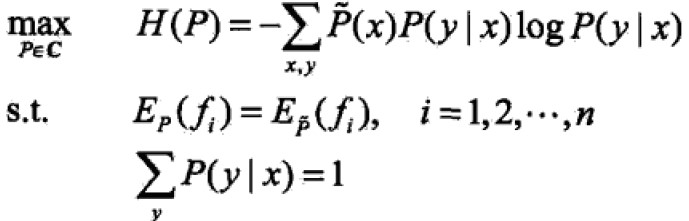等价于



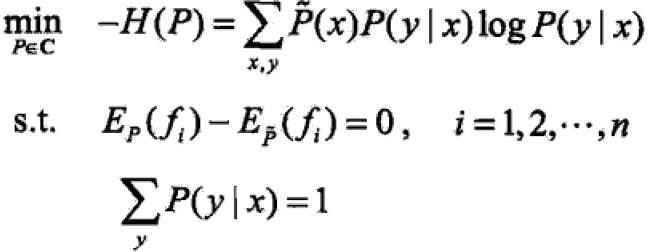
展示推导过程：

首先引入拉格朗日函数L(p,w)将约束问题转化为无约束最优化的对偶问题:

(可以发现跟高数中拉格朗日乘数法类似)

将原始问题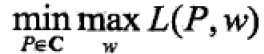转化为的对偶问题。

求解对偶问题：

首先求解min部分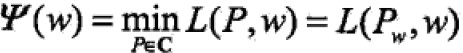，记作，其解记作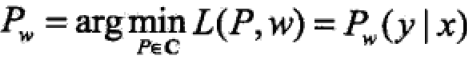

最小化问题就是求解其偏导=0，即



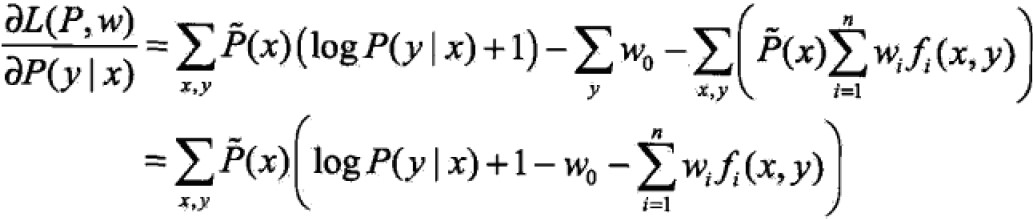
当P(x)>0时，Pw的解为：



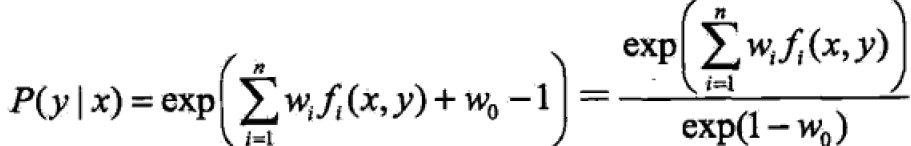
根据summation(P(y|x))=1，消去分母得

其中，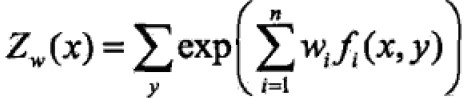

where，Zw(x)称为规范化因子，fi(x,y)是特征函数；wi是特征的权值。由上式表示的模型就是最大熵模型Pw，w是最大熵模型的参数向量。

其次求解max部分，，将其解记为w star： ，通过最优化算法求对偶函数ψ(w)的极大化

2.4 极大似然估计

证明：对偶函数的极大化等价于最大熵模型的极大似然估计

对数似然函数：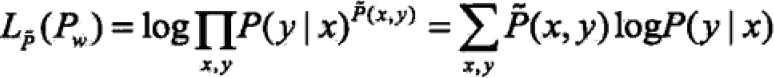

最大熵模型下，代入P(y|x)得到：

；

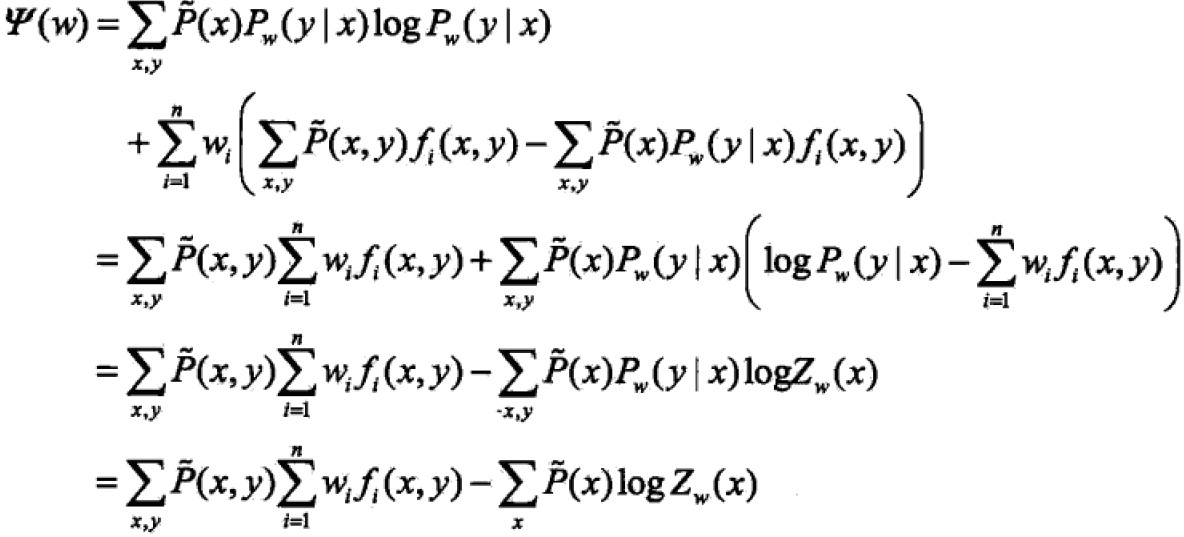（首尾步用到Summation(P)=1去掉w0）；

比较上二式得，

因此，最大熵模型就转化为具体求解对数似然函数或者对偶函数的极大化问题。

最大熵模型的一般形式：

，

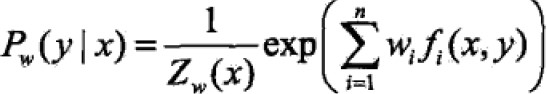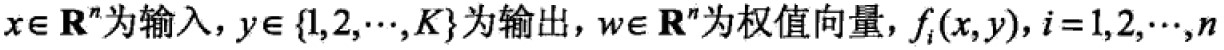为任意实数的特征函数。

3 模型训练算法

逻辑回归模型和最大熵模型最终都可以归结为以似然函数为目标函数的最优化问题，通常采用迭代法。从优化的观点来看，目标函数是光滑凸函数，很容易找到全局最优解。此处两个方法。

3.1 改进迭代尺度法(IIS)

improved iterative scaling是一种最大熵模型学习的最优化算法。由以上结论可知似然函数为：



目标是求得L的参数，即对数似然函数的极大值时的w hat。

IIS思想：



对于经验分布P(x,y),模型参数从w到w+δ，对数似然函数改变量：



利用不等式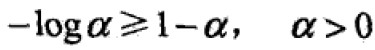求得该变量的下界：



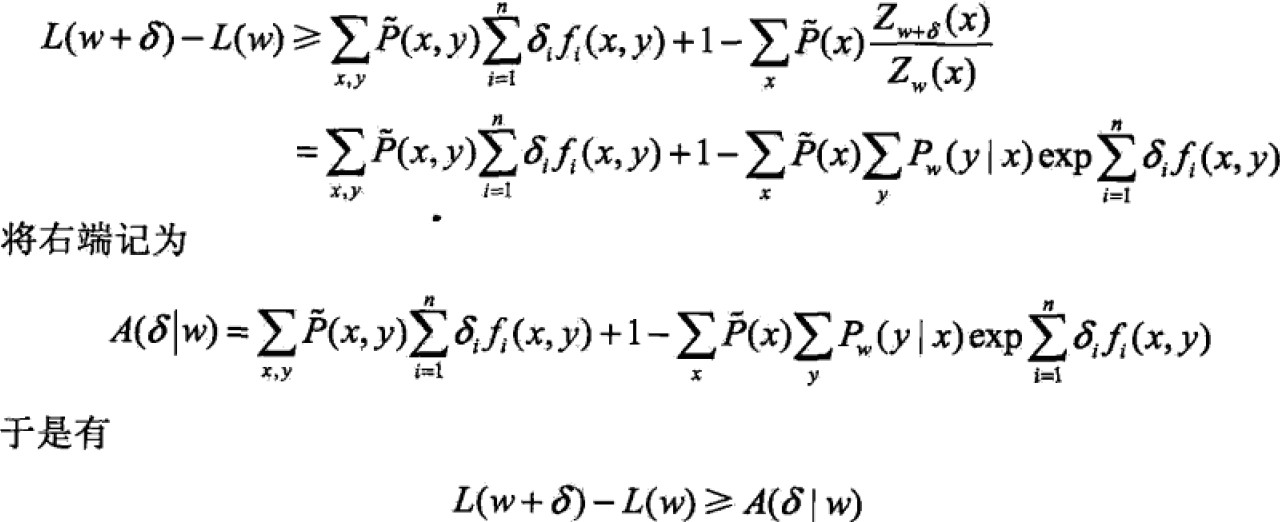
即，得到一个下界。如果使下界不断变大，相应的对数似然函数也会变大。A(δ|w)中δ是向量，同时优化不易，故每次只优化一个变量δi，固定其他。因此，如下处理：引入f#(x,y)=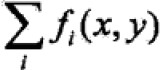,表示所有特征在(x,y)出现的次数（fi为二值函数），因此上界A改写为：

（乘一个f#，在除一个）

根据Jensen不等式：



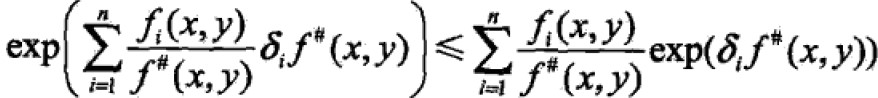
所以，



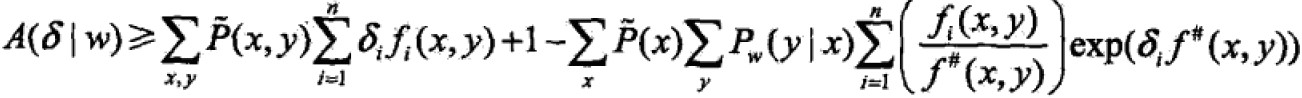
将右侧记为B(δ|w)，因此，似然函数变化量为：



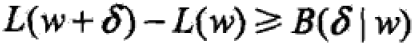
对B偏导δi

比用A直接偏导δ处简单

偏导=0得：

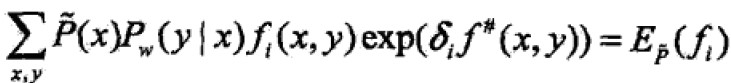依次求出delta然后w迭代

IIS算法：





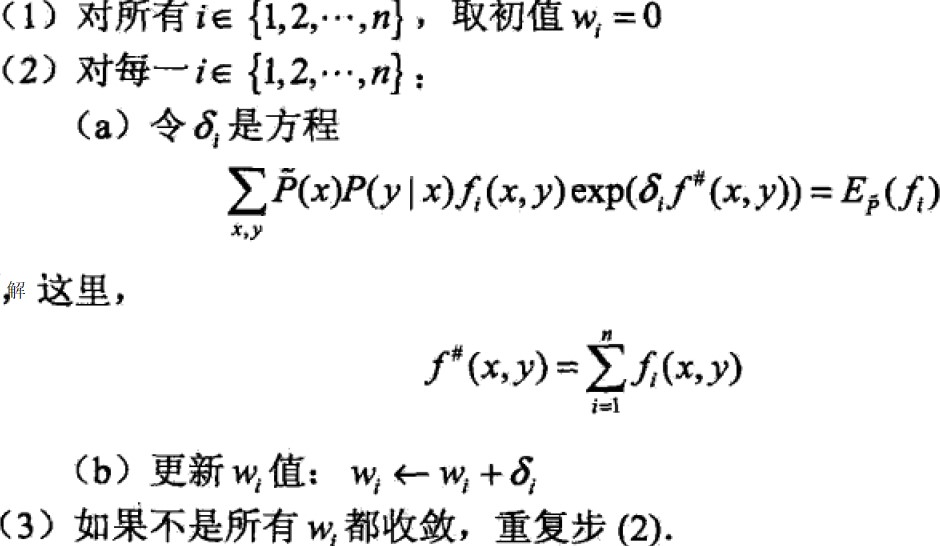
说明：关键步骤(a)，求解δi，

如果f#(x,y)是常数则f#(x,y)=M，那么δi可得：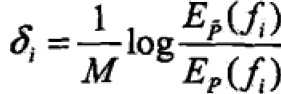

如果f#(x,y)不是常数，则必须通过数值计算来获取δi，最简单有效方法是牛顿法，另g(δi)=0表示(a)中等式，迭代公式为



选取合适的初值，方程有单根，牛顿法恒收敛，且收敛速度快。

3.2 拟牛顿法

最大熵模型：



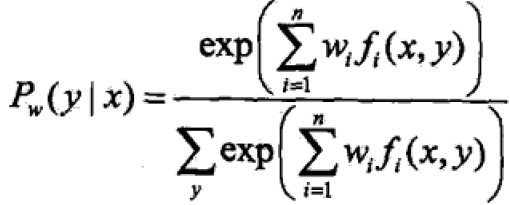
目标函数：



梯度：

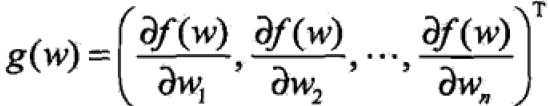where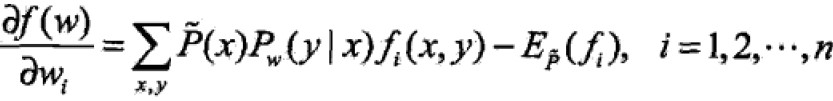

最大熵模型的BFGS算法：

---

附：更为详细的介绍：

牛顿法

拟牛顿法

DFP algorithm

BFGS algorithm

L-BFGS algorithm