Kosaraju 算法查找强连通分支

有向图 G = (V, E) 的一个强连通分支（SCC：Strongly Connected Components）是一个最大的顶点集合 C，C 是 V 的子集，对于 C 中的每一对顶点 u 和 v，有 u --> v 和 v --> u，亦即，顶点 u 和 v 是互相可达的。

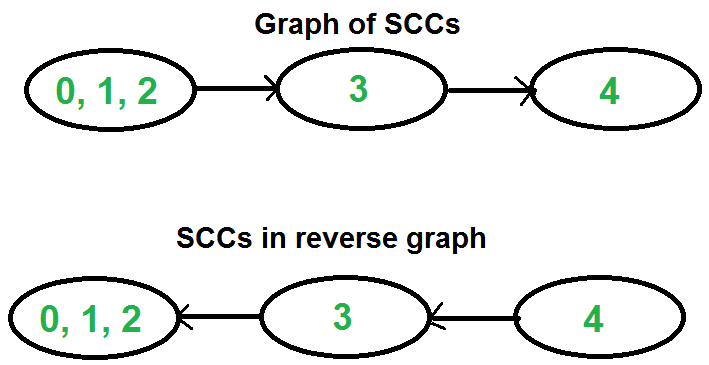
实际上，强连通分支 SCC 将有向图分割为多个内部强连通的子图。如下图中，整个图不是强连通的，但可以被分割成 3 个强连通分支。

通过 Kosaraju 算法，可以在 O(V+E) 运行时间内找到所有的强连通分支。Kosaraju 算法是基于深度优先搜索（DFS），算法的描述如下：

1. 创建一个空的栈 S，并做一次  DFS 遍历。在 DFS 遍历中，当在递归调用 DSF 访问邻接顶点时，将当前顶点压入栈中；
2. 置换图（Transpose Graph）；
3. 从栈 S 中逐个弹出顶点 v，以 v 为源点进行 DFS 遍历。从 v 开始的 DFS 遍历将输出 v 关联的强连通分支。

例如，对于上面的图做第一次 DFS 遍历，然后反转图，则可理解为整个图中的边的方向均反转了。

下面是 Kosaraju 算法的 C# 实现。

 using System;
 using System.Collections.Generic;
 using System.Linq;

 namespace GraphAlgorithmTesting
 {
   class Program
   {
     static void Main(string[] args)
     {
       Graph g = new Graph();
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );

       Console.WriteLine();
       Console.WriteLine("Graph Vertex Count : {0}", g.VertexCount);
       Console.WriteLine("Graph Edge Count : {0}", g.EdgeCount);
       Console.WriteLine();

       List<List<int>> sccs = g.Kosaraju();
       foreach (var scc in sccs)
       {
         foreach (var vertex in scc)
         {
           Console.Write("{0} ", vertex);
         }
         Console.WriteLine();
       }

       Console.ReadKey();
     }

     class Edge
     {
       public Edge(int begin, int end, int weight)
       {
         this.Begin = begin;
         this.End = end;
         this.Weight = weight;
       }

       public int Begin { get; private set; }
       public int End { get; private set; }
       public int Weight { get; private set; }

       public override string ToString()
       {
         return string.Format(
           "Begin[{0}], End[{1}], Weight[{2}]",
           Begin, End, Weight);
       }
     }

     class Graph
     {
       private Dictionary<int, List<Edge>> _adjacentEdges
         = new Dictionary<int, List<Edge>>();

       public Graph(int vertexCount)
       {
         this.VertexCount = vertexCount;
       }

       public int VertexCount { get; private set; }

       public IEnumerable<int> Vertices { get { return _adjacentEdges.Keys; } }

       public IEnumerable<Edge> Edges
       {
         get { return _adjacentEdges.Values.SelectMany(e => e); }
       }

       public int EdgeCount { get { return this.Edges.Count(); } }

       public void AddEdge(int begin, int end, int weight)
       {
         if (!_adjacentEdges.ContainsKey(begin))
         {
           var edges = new List<Edge>();
           _adjacentEdges.Add(begin, edges);
         }

         _adjacentEdges[begin].Add(new Edge(begin, end, weight));
       }

       public List<List<int>> Kosaraju()
       {
         Stack<int> stack = new Stack<int>();

         // Mark all the vertices as not visited (For first DFS)
         bool[] visited = new bool[VertexCount];
         for (int i = ; i < visited.Length; i++)
           visited[i] = false;

         // Fill vertices in stack according to their finishing times
         for (int i = ; i < visited.Length; i++)
           if (!visited[i])
             FillOrder(i, visited, stack);

         // Create a reversed graph
         Graph reversedGraph = Transpose();

         // Mark all the vertices as not visited (For second DFS)
         for (int i = ; i < visited.Length; i++)
           visited[i] = false;

         List<List<int>> sccs = new List<List<int>>();

         // Now process all vertices in order defined by Stack
         while (stack.Count > )
         {
           // Pop a vertex from stack
           int v = stack.Pop();

           // Print Strongly connected component of the popped vertex
           if (!visited[v])
           {
             List<int> scc = new List<int>();
             reversedGraph.DFS(v, visited, scc);
             sccs.Add(scc);
           }
         }

         return sccs;
       }

       void DFS(int v, bool[] visited, List<int> scc)
       {
         visited[v] = true;
         scc.Add(v);

         if (_adjacentEdges.ContainsKey(v))
         {
           foreach (var edge in _adjacentEdges[v])
           {
             if (!visited[edge.End])
               DFS(edge.End, visited, scc);
           }
         }
       }

       void FillOrder(int v, bool[] visited, Stack<int> stack)
       {
         // Mark the current node as visited and print it
         visited[v] = true;

         // Recur for all the vertices adjacent to this vertex
         if (_adjacentEdges.ContainsKey(v))
         {
           foreach (var edge in _adjacentEdges[v])
           {
             if (!visited[edge.End])
               FillOrder(edge.End, visited, stack);
           }
         }

         // All vertices reachable from v are processed by now,
         // push v to Stack
         stack.Push(v);
       }

       Graph Transpose()
       {
         Graph g = new Graph(this.VertexCount);

         foreach (var edge in this.Edges)
         {
           g.AddEdge(edge.End, edge.Begin, edge.Weight);
         }

         return g;
       }
     }
   }
 }

输出结果如下：

参考资料

• Connectivity in a directed graph
• Strongly Connected Components
• Tarjan's Algorithm to find Strongly Connected Components

本篇文章《Kosaraju 算法查找强连通分支》由 Dennis Gao 发表自博客园，未经作者本人同意禁止任何形式的转载，任何自动或人为的爬虫转载行为均为耍流氓。