tarjan算法，一个关于 图的联通性的神奇算法

一.算法简介

Tarjan 算法一种由Robert Tarjan提出的求解有向图强连通分量的算法，它能做到线性时间的复杂度。

我们定义：

如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

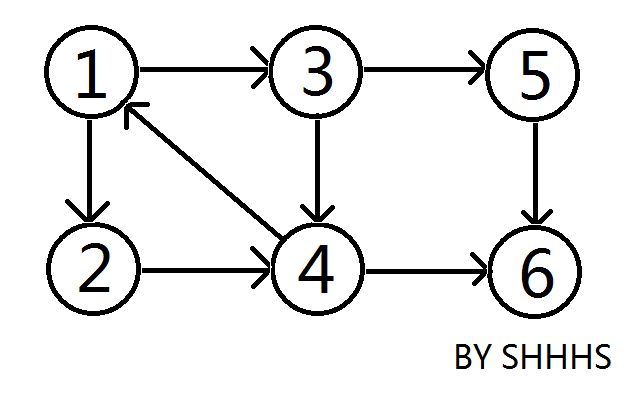
例如：在上图中，{1 , 2 , 3 , 4 } , { 5 }　,  { 6 } 三个区域可以相互连通，称为这个图的强连通分量。

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

再Tarjan算法中，有如下定义。

DFN[ i ] : 在DFS中该节点被搜索的次序(时间戳)

LOW[ i ] : 为i或i的子树能够追溯到的最早的栈中节点的次序号

当DFN[ i ]==LOW[ i ]时，为i或i的子树可以构成一个强连通分量。

二.算法图示

以1为Tarjan 算法的起始点，如图

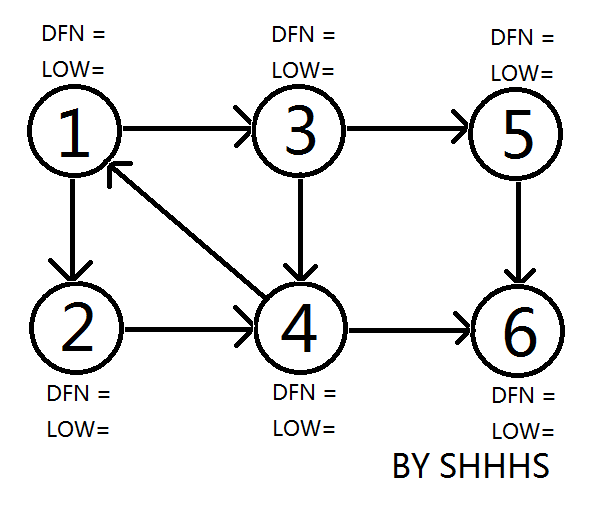
顺次DFS搜到节点6

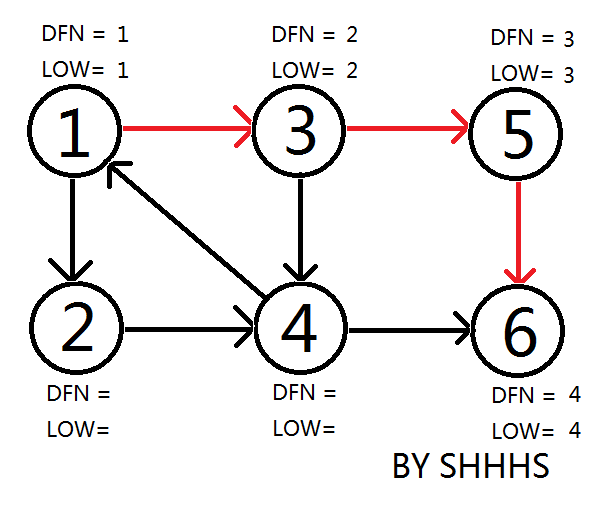
回溯时发现LOW[ 5 ]==DFN[ 5 ] ,  LOW[ 6 ]==DFN[ 6 ] ,则{ 5 } , { 6 } 为两个强连通分量。回溯至3节点，拓展节点4.

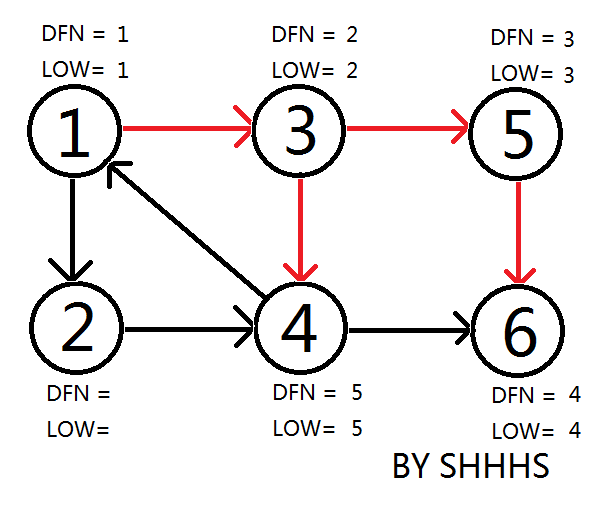
拓展节点1 ， 发现1再栈中更新LOW[ 4 ]，LOW[ 3 ] 的值为1

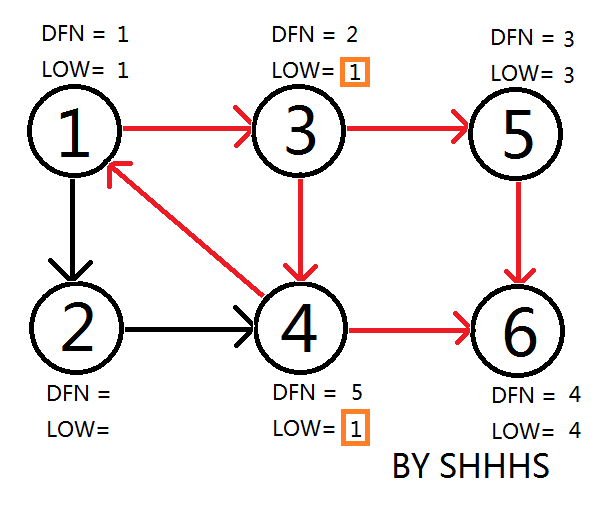
回溯节点1，拓展节点2

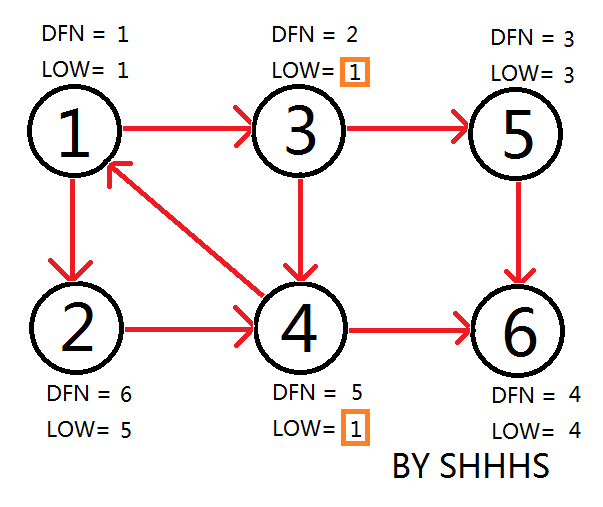
自此，Tarjan Algorithm 结束，{1 , 2 , 3 , 4 } , { 5 }　,  { 6 } 为图中的三个强连通分量。

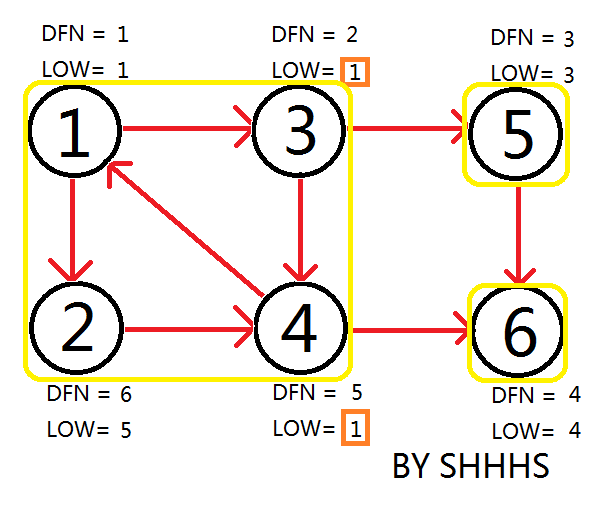
不难发现，Tarjan Algorithm 的时间复杂度为O(E+V).

学习处

模板：

 void dfs(int u)
 {
     times++;//记录dfn顺序
     dfn[u]=times;//赋值
     low[u]=times;//先赋初值
     vis[u]=true;//vis[i]用来判断i是否搜索过；
     insta[u]=true;//表示是否在栈中，true为在栈中；
     stack[top]=u;//栈顶
     top++;
     for(int i=head[u];i!=-;i=edge[i].next)// 以建图顺序枚举此点所连的边
     {
         int v=edge[i].to;//搜索到的点
         if(!vis[v])//如果未搜索过即未入栈
         {
             dfs(v);//继续以此点进行深搜
             low[u]=min(low[u],low[v]);//更新low值，此边为树枝边所以比较u此时的
         }                           // low值(未更新时就是其dfn值)和v的low值
         else
             if(insta[v]==true)//如果搜索过且在栈中，说明此边为后向边或栈中横叉边
             {
                 low[u]=min(low[u],dfn[v]);//更新low值，比较u此时的low值和v的dfn值
             }
     }

     if(low[u]==dfn[u])//相等说明找到一个强连通分量
     {
         while(top>&&stack[top]!=u)//开始退栈一直退到 u为止
         {
             top--;
             insta[stack[top]]=false;
         }
     }
 }

例题：

poj2186 - Popular Cows

题目大意：题目大意是：在一个牧群中，有N个奶牛，给定M对关系（A,B）表示A仰慕B，而且仰慕关系有传递性，问被所有奶牛（除了自己）仰慕的奶牛个数

解题思路：找出所有的连通分量，如果只有一个连通分量的出度为0，那么输出那个连通分量的点的个数即可,如果不唯一就输出0
因为连通分量的出度有两个的话，那么肯定至少存在一头牛不仰慕另外一头牛，所以我们至少保证要出度为0的连通分量唯一

解题思路：

1、用Tarjan求双连通分量然后缩成点。这些点会形成一棵树。

2、求树上的节点有多少个出度为零，如果有一个就输出那个点里包含的所有点（因为是缩点出来的树）。

注意：

1、给出的图会有不连通的可能，如果那样肯定输出零。因为不连通肯定不会有所有其他牛认为某只牛很牛的情况出现。

2、如果缩点后有多个出度为零的点，那么输出零。因为这样图虽然联通了，但是还是不会出现所有其他牛认为某只牛很牛的情况（自己画一下就知道啦）。

求强连通分量主要是为了简化图的构造，如果分量外的一个点能到达分量内的其中一个点，那么它必定能到达分量内的所有点，所以某种程度上，强连通分量可以简化成一个点。

#include <stdio.h>
#include <string.h>
const int MAXN = ;
const int MAXM = ;
struct node
{
    int to,next;
} edge[MAXM];
int n,m,head[MAXN],dfn[MAXN],low[MAXN],stack1[MAXN],num[MAXN],du[MAXN],vis[MAXN],cnt,time,top,cut;
void init()
{
    memset(dfn,,sizeof(dfn));
    memset(low,,sizeof(low));
    memset(head,-,sizeof(head));
    memset(vis,,sizeof(vis));
    memset(num,,sizeof(num));
    memset(du,,sizeof(du));
    cnt=;
    time=;
    top=;
    cut=;
}
void addedge(int u,int v)
{
    edge[cnt].to=v;
    edge[cnt].next=head[u];
    head[u]=cnt;
    cnt++;
}
int min(int a,int b)
{
    if(a>b)a=b;
    return a;
}
void dfs(int u,int fa)
{
    dfn[u]=time;
    low[u]=time;
    time++;
    vis[u]=;
    stack1[top]=u;
    top++;
    for(int i=head[u]; i!=-; i=edge[i].next)
    {
        int v=edge[i].to;
        if(!vis[v])
        {
            dfs(v,u);
            low[u]=min(low[u],low[v]);
        }
        else if(vis[v])
        {
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(low[u]==dfn[u])
    {
        cut++;
        while(top>&&stack1[top]!=u)
        {
            top--;
            vis[stack1[top]]=;
            num[stack1[top]]=cut;
        }
    }
}
int main()
{
    int i,u,v;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        init();
        for(i=; i<m; i++)
        {
            scanf("%d%d",&u,&v);
            addedge(u,v);
        }
        for(int i=; i<=n; i++)
        {
            if(!vis[i])
            {
                dfs(i,);
            }
        }
        for(i=; i<=n; i++)
        {
            for(int j=head[i]; j!=-; j=edge[j].next)
            {
                if(num[i]!=num[edge[j].to])
                {
                    du[num[i]]++;
                }
            }
        }
        int sum=,x;
        for(i=; i<=cut; i++)
        {
            if(!du[i])
            {
                sum++;
                x=i;
            }
        }
        if(sum==)
        {
            sum=;
            for(i=; i<=n; i++)
            {
                if(num[i]==x)
                {
                    sum++;
                }
            }
            printf("%d\n",sum);
        }
        else
        {
            puts("");
        }
    }
    return ;
}