五、c++实现离散傅里叶变换

C++离散傅里叶变换

一、序言：

该教程基于之前的图像处理类MYCV，是对其的补充。

二、设计目标

对图像进行简单的离散傅里叶变换，并输出生成的频谱图。

三、需要提前掌握的知识

二维傅里叶变换公式：

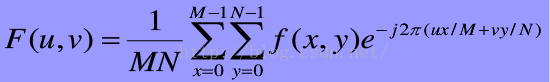
四、详细步骤

1．首先定义一个方法，该方法对输入的图像进行傅里叶变换

输入：MyImage 源图像

输出：ComplexNu 进行离散傅里叶变换后的复数数组

定义：

static ComplexNumber* Dft2(MyImage const &Scr);

实现：

ComplexNumber* MyCV::Dft2(MyImage const &Scr)

{

    int width = Scr.m_width;

    int height = Scr.m_height;

    // 将 scr_data 转化为灰度

    MyImage *grayimage = Gray(Scr);

    unsigned char* gray_data = grayimage->m_data;

    int gray_bytesPerLine = grayimage->m_bytesPerLine;

    // 将 gray_data 转化为 double 型，并去掉用于填充的多余空间

    double *double_data = new double[width*height];

    for(int i=;i<height;i++)

        for(int j=;j<width;j++)

        {

            double_data[i*width+j]=(double)gray_data[i*gray_bytesPerLine+j];

        }

    // 对 double_data 进行傅里叶变换

    ComplexNumber *dft2_data = new ComplexNumber[width*height];

    double fixed_factor_for_axisX = (- * PI) / height;

    // evaluate -i2π/N of -i2πux/N, and store the value for computing efficiency

    double fixed_factor_for_axisY = (- * PI) / width;

    // evaluate -i2π/N of -i2πux/N, and store the value for computing efficiency

    for (int u = ; u<height; u++) {

            for (int v = ; v<width; v++) {

                for (int x = ; x<height; x++) {

                    for (int y = ; y<width; y++) {

                        double powerX = u * x * fixed_factor_for_axisX; // evaluate -i2πux/N

                        double powerY = v * y * fixed_factor_for_axisY; // evaluate -i2πux/N

                        ComplexNumber cplTemp;

                        cplTemp.m_rl = double_data[y + x*width] * cos(powerX + powerY);

                        // evaluate f(x) * e^(-i2πux/N), which is equal to f(x) * (cos(-i2πux/N)+sin(-i2πux/N)i) according to Euler's formula

                        cplTemp.m_im = double_data[y + x*width] * sin(powerX + powerY);

                        dft2_data[v + u*width] = dft2_data[v + u*width] + cplTemp;

                    }

                }

            }

        }

    // 返回傅里叶数组

    return dft2_data;

}

2．为了让傅里叶变换可视化，旭阳对其进行标准化和中性化

输入：ComplexNumber 离散傅里叶变换生成的复数数组

输出：MyImage 可视化后的图像

定义：

static MyImage* Dft22MyImage(ComplexNumber *Scr,int width,int height);

实现：

MyImage* MyCV::Dft22MyImage(ComplexNumber *Scr, int const width, int const height)

{

    // 将傅里叶数组归一化

    // 取模

    double mold[width*height];

    for(int i =  ;i<width*height;i++)

    {

        mold[i] = Scr[i].get_mold();

    }

    // 获取最小值

    double min = mold[];

    for(int i = ;i<width*height;i++)

    {

        if(mold[i]<min)

            min = mold[i];

    }

    // 获取去掉前几大值的最大值

    double maxqueue[] = {.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.,.},max;

    for(int i = ;i<width*height;i++){

        if(mold[i]>maxqueue[])

            maxqueue[] = mold[i];

    }

    for(int j =;j<;j++){

        for(int i = ;i<width*height;i++){

            if(mold[i]>maxqueue[j]&&mold[i]<maxqueue[j-])

                maxqueue[j] = mold[i];

        }

    }

    max = maxqueue[];

    unsigned char *normalized_data = new unsigned char[width*height];

    for(int i=;i<height;i++)

        for(int j=;j<width;j++)

        {

            unsigned char t = (unsigned char)((mold[i*width+j]-min)/(max-min)*);

            if(t>)

                t = ;

            normalized_data[i*width+j]=t;

        }

    // 将图像中心化

    unsigned char* center_data = new unsigned char[width*height];

    for (int u = ; u<height; u++)

        {

        for (int v = ; v<width; v++) {

            if ((u<(height / )) && (v<(width / ))) {

                center_data[v + u*width] =

                    normalized_data[width /  + v + (height /  + u)*width];

            }

            else if ((u<(height / )) && (v >= (width / ))) {

                center_data[v + u*width] =

                    normalized_data[(v - width / ) + (height /  + u)*width];

            }

            else if ((u >= (height / )) && (v<(width / ))) {

                center_data[v + u*width] =

                    normalized_data[(width /  + v) + (u - height / )*width];

            }

            else if ((u >= (height / )) && (v >= (width / ))) {

                center_data[v + u*width] =

                    normalized_data[(v - width / ) + (u - height / )*width];

            }

        }

    }

    // 向中心化的数组填充空间

    int bytesPerLine = (width*+)/*;

    unsigned char *dst_data = new unsigned char[bytesPerLine*height];

    for(int i=;i<height;i++)

        for(int j=;j<width;j++)

        {

            dst_data[i*bytesPerLine+j] = center_data[i*width+j];

        }

    return new MyImage(dst_data,width,height,MyImage::format::GRAY8);

}

至此，离散傅里叶变换的方法实现完成，效果图如下：

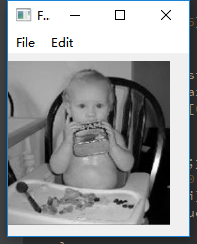
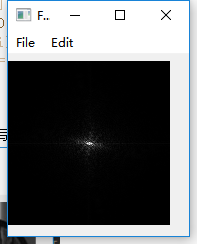
如果上述教程或代码中有任何错误，欢迎批评和指证。