bzoj 2618 半平面交模板+学习笔记

题目大意

给你n个凸多边形，求多边形的交的面积

分析

题意\(=\)给你一堆边，让你求半平面交的面积

做法

半平面交模板

1.定义半平面为向量的左侧

2.将所有向量的起点放到一个中心,以中心参照进行逆时针极角排序

但是直接按叉积排序会转圈圈

于是我们从\(x\)轴负半轴开始逆时针旋转，将坐标轴分为上下两部（\(x\)轴属于下部）

当两个向量终点的\(y\)都在x轴上时，按x从小到大排

当两个向量终点同在上部/同在下部时，按叉积排（平行按左右排）

当一上一下时，下部的排前

注意：快排时像我这样贪方便，在cmp里swap一下想都不想的人也是很罕见的

3.考虑下面这样一幅图



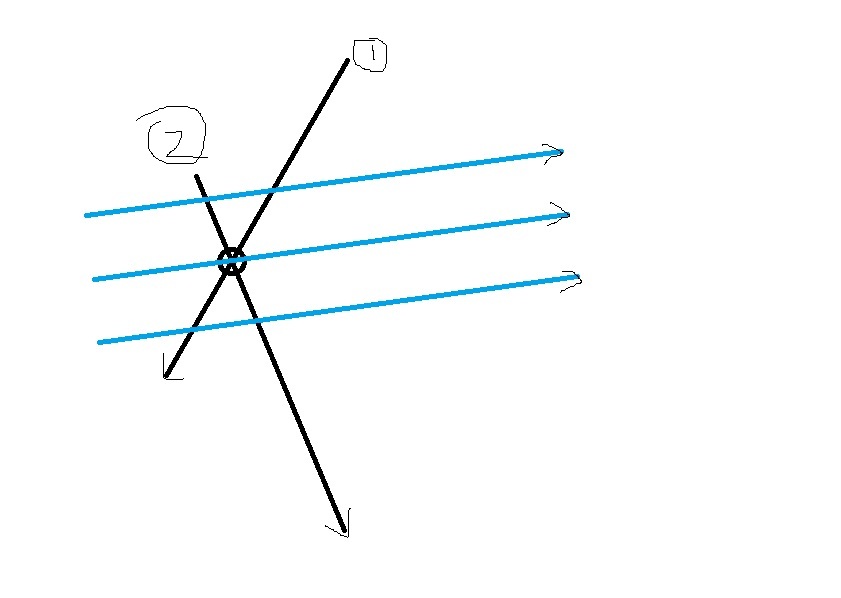
黑色为原半平面交的边界，蓝色为新加入的向量

不难发现当之前交点在蓝色右边时，向量1要被删掉

这样的话，每次新加入向量，就会删掉在向量右边的交点(线上的也要删)

最后会在所有交点的右边，画幅图出来发现这和凸包是非常像的

然后考虑下面的一幅图



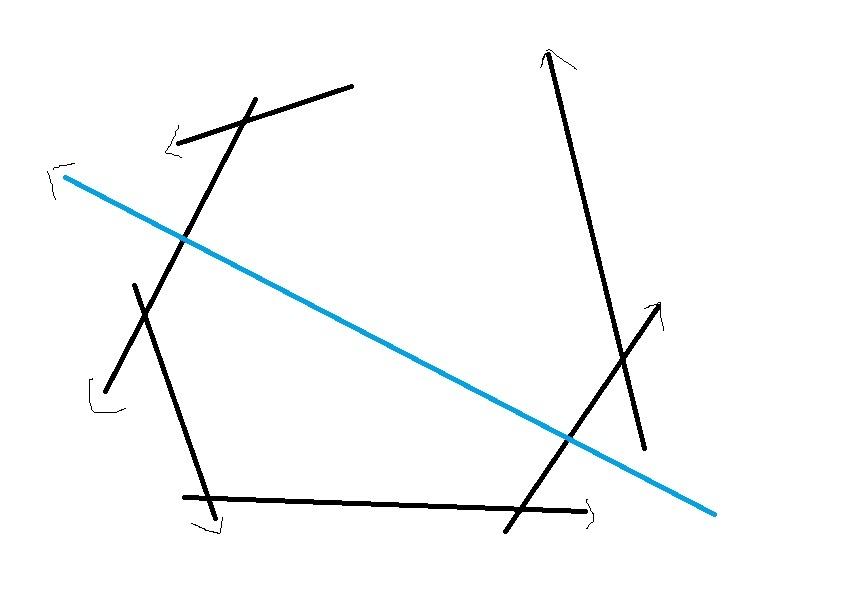
发现我们维护的凸包首尾都是要删除的

所以我们要写一个双端队列

4.考虑平行的两个向量，一定是保留最左的一个

5.考虑下面这幅图



图上的边搞完之后都还是在双端队列里的

但是：最后带红色标记的那一条边是无效的，为什么呢？

因为凸包首尾是连起来的！

所以最后还要模拟插入队头，把队尾中多余的半平面去掉

6.如果题目没有保证半平面封闭，就加上一个超大的四边形限制

推广

uoj的一篇博客写的很棒，证明也很棒，还提到了一种先求上凸壳，再求下凸壳，再把两边多出来的部分删掉的方法   搓这

solution

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <cmath>
#include <algorithm>
using namespace std;
typedef double db;
const int M=507;
inline int rd(){
    int x=0;bool f=1;char c=getchar();
    for(;!isdigit(c);c=getchar()) if(c=='-') f=0;
    for(;isdigit(c);c=getchar()) x=x*10+c-48;
    return f?x:-x;
}
int n,m,tt;
struct pt{
    db x,y;
    pt(db xx=0,db yy=0){x=xx;y=yy;}
}p[M],a[M];
pt operator +(pt x,pt y){return pt(x.x+y.x,x.y+y.y);}
pt operator -(pt x,pt y){return pt(x.x-y.x,x.y-y.y);}
pt operator *(pt x,db d){return pt(x.x*d,x.y*d);}
pt operator /(pt x,db d){return pt(x.x/d,x.y/d);}
db slop(pt x){return x.y/x.x;}
db dot(pt x,pt y){return x.x*y.x+x.y*y.y;}
db det(pt x,pt y){return x.x*y.y-x.y*y.x;}
db len(pt x){return sqrt(dot(x,x));}
db dis(pt x,pt y){return len(y-x);}
db area(pt x,pt y,pt z){return det(y-x,z-x);}
struct line{
    pt P,v;
    line(pt PP=pt(),pt vv=pt()){P=PP;v=vv;}
}l[M],s[M];
pt inter(line x,line y){
    pt u=x.P-y.P;
    db t=det(u,y.v)/det(y.v,x.v);
    return x.P+x.v*t;
}
bool parallel(line x,line y){return det(y.v,x.v)==0;}
bool lineleft(line x,line y){
	db tp=det(x.v,y.v);
	return (tp>0)||((tp==0)&&det(x.v,y.P-x.P)>0);
}
bool ptright(pt x,line y){return det(y.v,x-y.P)<=0;}///<=
bool cmp(line x,line y){//极角排序
    if(x.v.y==0 && y.v.y==0) return x.v.x<y.v.x;//y都为0
    if(x.v.y<=0 && y.v.y<=0) return lineleft(x,y);//同在上部
    if(x.v.y>0  && y.v.y>0 ) return	lineleft(x,y);//同在下部
    return x.v.y<y.v.y;//一上一下
}
void hpi(){//half-plane intersection
    sort(l+1,l+m+1,cmp);//sort
    int tp=0,i;
    for(i=1;i<=m;i++){
        if(i==1||!parallel(l[i],l[i-1])) tp++;//平行特判
        l[tp]=l[i];
    }
    m=tp;
    int L=1,R=2;
    s[1]=l[1],s[2]=l[2];
    for(i=3;i<=m;i++){
        while(L<R && ptright(inter(s[R],s[R-1]),l[i])) R--;
        while(L<R && ptright(inter(s[L],s[L+1]),l[i])) L++;
        s[++R]=l[i];
    }
    while(L<R && ptright(inter(s[R],s[R-1]),s[L])) R--;//最后删除无用平面
    if(R-L<=1){//若半平面交退化为点或线
        puts("0.000");
        return;
    }
    tp=0;
    s[L-1]=s[R];
    for(i=L;i<=R;i++) a[++tp]=inter(s[i],s[i-1]);//求出相邻两边的交点，转化为凸包的记录方法
    db ans=0;
    for(i=3;i<=tp;i++) ans+=area(a[1],a[i-1],a[i])*0.5;
    printf("%.3lf",ans);//求面积
}
int main(){
    int i,x,y,z,st;
    tt=rd();
    n=m=0;
    while(tt--){
        z=rd();
        st=n+1;
        while(z--){
            x=rd(),y=rd();
            p[++n]=pt(x,y);
            if(n>st) l[++m]=line(p[n-1],p[n]-p[n-1]);
        }
        l[++m]=line(p[n],p[st]-p[n]);
    }
    hpi();
    return 0;
}