POJ 3608 凸包间最短距离（旋转卡壳）

Bridge Across Islands

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 11539		Accepted: 3395		Special Judge

Description

Thousands of thousands years ago there was a small kingdom located in the middle of the Pacific Ocean. The territory of the kingdom consists two separated islands. Due to the impact of the ocean current, the shapes of both the islands became convex polygons. The king of the kingdom wanted to establish a bridge to connect the two islands. To minimize the cost, the king asked you, the bishop, to find the minimal distance between the boundaries of the two islands.

Input

The input consists of several test cases.
Each test case begins with two integers N, M. (3 ≤ N, M ≤ 10000)
Each of the next N lines contains a pair of coordinates, which describes the position of a vertex in one convex polygon.
Each of the next M lines contains a pair of coordinates, which describes the position of a vertex in the other convex polygon.
A line with N = M = 0 indicates the end of input.
The coordinates are within the range [-10000, 10000].

Output

For each test case output the minimal distance. An error within 0.001 is acceptable.

Sample Input

4 4
0.00000 0.00000
0.00000 1.00000
1.00000 1.00000
1.00000 0.00000
2.00000 0.00000
2.00000 1.00000
3.00000 1.00000
3.00000 0.00000
0 0

Sample Output

1.00000

Source

POJ Founder Monthly Contest – 2008.06.29, Lei Tao

 

图示：

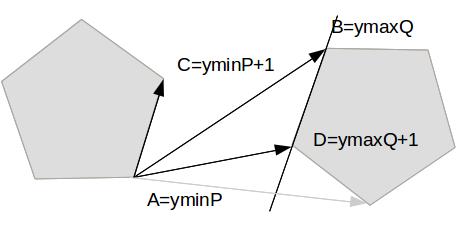
思路：找到凸包 p 的 y 值最小点 yminP 和 q 的 y 值最大点ymaxQ，然后分别做切如图。那么AC×AD>AC×AB则说明B还不是离AC最近的点，所以++ymaxQ。

否则用 AC和 BD 两个线段的距离更新最近距离，并且++yminP，即考察P的下一条边。

具体实现时，同时旋转体现为逐步选取逆时针方向上的下一个顶点作为C或D、A或B,其实选择卡壳就是只要找到"当前向量面积不小于下一个向量面积"即可,再求两条线段间的最短距离。

代码：

 //#include "bits/stdc++.h"
 #include "cstdio"
 #include "map"
 #include "set"
 #include "cmath"
 #include "queue"
 #include "vector"
 #include "string"
 #include "cstring"
 #include "time.h"
 #include "iostream"
 #include "stdlib.h"
 #include "algorithm"
 #define db double
 #define ll long long
 #define vec vector<ll>
 #define mt  vector<vec>
 #define ci(x) scanf("%d",&x)
 #define cd(x) scanf("%lf",&x)
 #define cl(x) scanf("%lld",&x)
 #define pi(x) printf("%d\n",x)
 #define pd(x) printf("%f\n",x)
 #define pl(x) printf("%lld\n",x)
 //#define rep(i, x, y) for(int i=x;i<=y;i++)
 #define rep(i,n) for(int i=0;i<n;i++)
 const int n   = 1e4 + ;
 const int mod = 1e9 + ;
 const int mOD = mod - ;
 const db  eps = 1e-;
 const db  PI  = acos(-1.0);
 const int inf=0x3f3f3f3f;
 using namespace std;
 struct P
 {
     db x, y;
     P() {}
     P(db x, db y) : x(x), y(y) {}
     P operator + (const P& p){ return P(x + p.x, y + p.y); }
     P operator - (const P& p){ return P(x - p.x, y - p.y); }
     P operator * (const db& d){ return P(x * d, y * d); }
     bool operator < (const P& a) const
     {
         if (x != a.x) return x < a.x;
         else return y < a.y;
     }
     db dot(const P& p) { return x * p.x + y * p.y; }
     db det(const P& p) { return x * p.y - y * p.x; }
 };
 P p[n], q[n];
 // 向量AB 与 AC 的叉积 如果叉积大于0，那么C在向量AB的逆时针方向，叉积小于0则在AB的顺时针方向。如果叉积等于0，则ABC共线。
  db cross(P A, P B, P C) {return (B - A).det(C - A); }
 // 向量AB 与 AC 的点积 如果点积的结果为0，那么这两个向量互相垂直
  db mul(P A, P B, P C)  {return (B - A).dot(C - A); }
 // 两点距离
  db dis(P A, P B){return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y)); }

 // 逆时针排序
  void csort(P* p, int n)
 {
     for (int i = ; i < n - ; ++i)
     {
         db tmp = cross(p[i], p[i + ], p[i + ]);
         if (tmp > eps) return;
         else if (tmp < -eps)
         {
             reverse(p, p + n);
             return;
         }
     }
 }

 //计算C点到线段AB的最短距离
  db ptl(P A, P B, P C)
 {
     if (dis(A, B) < eps) return dis(B, C);
     if (mul(A, B, C) < -eps) return dis(A, C);
     if (mul(B, A, C) < -eps) return dis(B, C);
     return fabs(cross(A, B, C) / dis(A, B));
 }
 //求一条线段的两端点到另外一条线段的距离，反过来一样，共4种情况
  db ltl(P A, P B, P C, P D)
 {
     return min(min(ptl(A, B, C), ptl(A, B, D)), min(ptl(C, D, A), ptl(C, D, B)));
 }
 db solve(P* p, P* q, int n, int m)
 {
     int pmi = , qmx = ;
     for (int i = ; i < n; ++i) if (p[i].y < p[pmi].y) pmi = i;    // P上y坐标最小的顶点
     for (int i = ; i < m; ++i) if (q[i].y > q[qmx].y) qmx = i; // Q上y坐标最大的顶点
     p[n] = p[];    // 为了方便，避免求余
     q[m] = q[];
     db tmp, ans = inf;
     for (int i = ; i < n; ++i)
     {
         while (tmp = cross(p[pmi],p[pmi + ], q[qmx + ]) - cross(p[pmi],p[pmi + ], q[qmx]) > eps) qmx = (qmx + ) % m;
         ans = min(ans, ltl(p[pmi], p[pmi + ], q[qmx], q[qmx + ]));
         pmi = (pmi + ) % n;
     }
     return ans;
 }
 int main()
 {
     int n, m;
     while (~scanf("%d%d", &n, &m) && n + m)
     {
         for (int i = ; i < n; ++i) cd(p[i].x),cd(p[i].y);
         for (int i = ; i < m; ++i) cd(q[i].x),cd(q[i].y);
         csort(p, n);
         csort(q, m);
         printf("%.5lf\n", solve(p, q, n, m));
     }
     return ;
 }