机器学习实战 -- 决策树(ID3)

 

ID3是什么我也不知道，不急，知道他是干什么的就行

 

ID3是最经典最基础的一种决策树算法，他会将每一个特征都设为决策节点，有时候，一个数据集中，某些特征属性是不必要的或者说信息熵增加的很少，这种决策信息是可以合并的修剪的，但是ID3算法并不会这么做

 

决策树的核心论点是香农信息论，借此理论得出某种分类情况下的信息熵

 

 

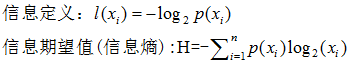
某种决策下，分类趋向于统一，则香农熵很小（熵描述杂乱无序的程度，如果'YES', 'NO' 可能性对半分，那么这个分类决策最终是趋向于杂乱的熵值会很大， 只出现 'YES' 那么表示这个决策的结果趋向于一个统一的结果，固定，那么熵就很小）

 

综上：某个决策节点下，信息熵越小，说明这个决策方式越好

 

整个决策树分为三个部分：1.学习出决策树 2.绘制决策树 3.存储决策树

 

比起sklearn这个决策树更简单，没有考虑基尼系数，只关注信息熵

  1. from math import log  
  2.   
     
  3. ''''' 
  4. 计算香农熵 
  5. '''  
  6. def calcShannonEnt(dataset):  
  7.     ''''' 
  8. dataset    —— 数据集 eg:[[f1,f2,f3,L1],[f1,f2,f3,L2]] 
  9.                 f表示特征，L表示标签 
  10.                  
     
  11. shannonEnt —— 香农熵 
  12.     '''  
  13.     numEntries=len(dataset) #统计数据集中样本数量  
  14.     labelCounts={}  
  15.     for featVec in dataset:  
  16.         currentLabel=featVec[-1]  
  17.         if currentLabel not in labelCounts.keys():  
  18.             labelCounts[currentLabel]=0  
  19.         labelCounts[currentLabel] +=1  
  20.   
     
  21. #for循环统计数据集中各个标签量的个数。如：有几种情况下是'no'  
  22.   
     
  23.     shannonEnt=0.0  
  24.     for key in labelCounts:  
  25.         prob=float(labelCounts[key])/numEntries  
  26.         shannonEnt-=prob*log(prob,2)  
  27.   
     
  28. #香农熵计算见word  
  29.     return shannonEnt  
  30.   
     
  31. ''''' 
  32. 根据特征值划分数据集 
  33. '''  
  34. def splitDataSet(dataSet,axis,value):  
  35.     ''''' 
  36. dataset ——要数据集 
  37. axis    ——要从哪一个特征划分 
  38. value   ——精确到特征下的哪一个值 
  39. 个特征值为0时划分 
  40. 实际效果：将每个样本中特征值符合(axis,value)定位条件的样本找出来，并删除这个特征 
  41.  
     
  42. retDataSet——按照特征值划分出的数据子集 
  43.     '''  
  44.     retDataSet=[]  
  45.     for featVec in dataSet:  
  46.         if featVec[axis] == value: #找到定位点  
  47.             _=featVec.copy()       #拷贝，防止删除特征时影响到原数据集  
  48.             del _[axis]            #删除特征  
  49.             retDataSet.append(_)   #将该样本添加到子集中  
  50.     return retDataSet  
  51.   
     
  52.   
     
  53. ''''' 
  54. 判断当前数据集中最好的数据划分形式 
  55. '''  
  56. def Best(dataSet):  
  57.     numFeatures=len(dataSet[0])-1  
  58.     baseEntropy=calcShannonEnt(dataSet)  
  59.     bestInfoGain=0.0  
  60.     bestFeature=-1  
  61.     for i in range(numFeatures):  
  62.         #将每个特征都作为决策节点进行一一尝试，找出最佳  
  63.         featList=[example[i] for example in dataSet]  
  64.         #提取每个样本中第i个特征  
  65.         uniqueVals=set(featList)  
  66.         newEntropy=0.0  
  67.         for value in uniqueVals:  
  68.             #一个特征下有几个特征值，分特征值进行香农熵计算  
  69.             subDataSet=splitDataSet(dataSet,i,value)  
  70.             prob=len(subDataSet)/float(len(dataSet))  
  71.             newEntropy+=prob*calcShannonEnt(subDataSet)  
  72.         infoGain=baseEntropy-newEntropy  
  73.         if(infoGain>bestInfoGain):  
  74.             bestInfoGain=infoGain  
  75.             bestFeature=i  
  76.         return bestFeature  
  77.   
     
  78. ''''' 
  79. 多数表决 
  80. 当所有特征都决策完时，标签还没有统一，此时就使用多数服从少数的原则 
  81. 该分类下，哪种标签多，就以哪种标签作为分类依据 
  82. '''  
  83. def majorityCnt(classList):  
  84.       
     
  85.     ''''' 
  86. classlist ——关于标签的列表 
  87.  
     
  88. 书上的 
  89.     classCount={} 
  90.     for vote in classList: 
  91.         if vote not in classCount.keys(): 
  92.             classCount[vote]=0 
  93.         classCount[vote]+=1 
  94.     sortedClassCount=sorted(classCount.items(), 
  95.         key=operator.itemgetter(1), 
  96.         reverse=True) 
  97.     return sortedClassCount[0][0] 
  98.     '''  
  99.     value=0  
  100.     for i in classList:  
  101.         if classlist.count(i) >value:  
  102.             max_label=i  
  103.             value=classlist.count(i)  
  104.     return max_label  
  105.   
     
  106. def createTree(dataSet,labels):  
  107.     classList=[example[-1] for example in dataSet]  
  108.     #标签中只有一种了，说明到叶子节点了，直接返回标签  
  109.     if len(set(classList)) ==1:  
  110.         return classList[0]  
  111.     #样本中没有特征了，只能多数服从小数了  
  112.     if len(dataSet[0])==1:  
  113.         return majorityCnt(classList)  
  114.     #先找好决策节点  
  115.     bestFeat=Best(dataSet)  
  116.     bestFeatlabel=labels[bestFeat]  
  117.     myTree={bestFeatlabel:{}}  
  118.     del labels[bestFeat]#此处，标签列表要随着子集变化而变化  
  119.   
     
  120.     #找出决策节点后，继续深入分析特征值  
  121.     featValues=[example[bestFeat] for example in dataSet]  
  122.     uniqueVals=set(featValues)  
  123.     #遍历特征值进行树创建  
  124.     for value in uniqueVals:  
  125.         subLabels=labels[:]   
  126.         #此处，记得保留最顶层的标签，不能递归的时候让孙子辈的子节点把爷爷辈的标签给改了  
  127.         myTree[bestFeatlabel][value]=createTree(  
  128.             splitDataSet(dataSet,bestFeat,value),  
  129.             subLabels)  
  130.   
     
  131.     return myTree  
  132.   
     
  133.   
     
  134. ''''' 
  135. ------------------------- 
  136. 绘制决策树 
  137. 主要是接通matplotlib中的annotate函数来绘画 
  138. 实际上现在可以借用graphviz来绘制，没去了解这个东西 
  139. ------------------------- 
  140. '''  
  141. import matplotlib.pyplot as plt  
  142. #建立绘图参数  
  143. decisionNode=dict(boxstyle='sawtooth',fc='0.8')  
  144. leafNode=dict(boxstyle='round',fc='0.8')  
  145. arrow_args=dict(arrowstyle='<-')  
  146.   
     
  147. #创建图纸，以及设立好初始xoff和yoff  
  148. def createPlot(inTree):  
  149.     fig=plt.figure(1,facecolor='white')  
  150.     fig.clf()  
  151.     axprops=dict(xticks=[],yticks=[])  
  152.     createPlot.ax1=plt.subplot(111,frameon=False,**axprops)  
  153.     plotTree.totalW=float(getNumLeafs(inTree))  
  154.     plotTree.totalD=float(getTreeDepth(inTree))  
  155.     plotTree.xoff=-0.5/plotTree.totalW  
  156.     plotTree.yoff=1.0  
  157.     plotTree(inTree,(0.5,1.0),'')  
  158.     plt.show()  
  159.       
     
  160. #递归绘制决策树，遇到决策节点就递归，所以最后会有那条+1.0/plotTree.totalD语句返回分叉点  
  161. def plotTree(myTree,parentPt,nodeTxt):  
  162.     numLeafs=getNumLeafs(myTree)  
  163.     depth=getTreeDepth(myTree)  
  164.     firstStr=list(myTree.keys())[0]  
  165.     cntrPt=(plotTree.xoff+(1+float(numLeafs))/2.0/plotTree.totalW,plotTree.yoff)  
  166. #上面关于子节点的x值计算，有点绕，可以慢慢调整参数值，知道如何影响决策图的  
  167.     plotMidText(cntrPt,parentPt,nodeTxt)  
  168.     plotNode(firstStr,cntrPt,parentPt,decisionNode)  
  169.     secondDict=myTree[firstStr]  
  170.   
     
  171.     plotTree.yoff=plotTree.yoff-1.0/plotTree.totalD  
  172.     for key in secondDict.keys():  
  173.         if type(secondDict[key])==dict:  
  174.             plotTree(secondDict[key],cntrPt,str(key))  
  175.         else:  
  176.             plotTree.xoff=plotTree.xoff+1.0/plotTree.totalW  
  177.             plotNode(secondDict[key],(plotTree.xoff,plotTree.yoff),cntrPt,leafNode)  
  178.             plotMidText((plotTree.xoff,plotTree.yoff),cntrPt,str(key))            
  179.     plotTree.yoff=plotTree.yoff+1.0/plotTree.totalD  
  180.   
     
  181.   
     
  182. ''''' 
  183. 获取叶子节点数量 
  184. 遍历所有节点，只要不是dict即不是决策节点，numLeafs就+1 
  185. '''  
  186. def getNumLeafs(myTree):  
  187.     numLeafs=0  
  188.     firstStr=list(myTree.keys())[0]  
  189.     secondDict=myTree[firstStr]  
  190.     for key in secondDict.keys():  
  191.         if type(secondDict[key]) ==dict:  
  192.             numLeafs+=getNumLeafs(secondDict[key])  
  193.         else:  
  194.             numLeafs+=1  
  195.     return numLeafs  
  196.   
     
  197. ''''' 
  198. 获取决策节点的数量 
  199. 遍历所有节点，只要是dict，即决策节点，深度就+1 
  200. 注意的是，没遍历一个特征就需要和储存的depth比较一番，选取最深的才是树的深度 
  201. '''  
  202. def getTreeDepth(myTree):  
  203.     maxDepth=0  
  204.     firstStr=list(myTree.keys())[0]  
  205.     secondDict=myTree[firstStr]  
  206.     for key in secondDict.keys():  
  207.         if type(secondDict[key])==dict:  
  208.             thisTreeDepth=1+getTreeDepth(secondDict[key])  
  209.         else:  
  210.             thisTreeDepth=1  
  211.         if thisTreeDepth>maxDepth:  
  212.             maxDepth=thisTreeDepth  
  213.     return maxDepth  
  214.   
     
  215. #在连接线的中间标注特征值  
  216. def plotMidText(cntrPt,parentPt,txtString):  
  217.     xmid=(parentPt[0]-cntrPt[0])/2.0+cntrPt[0]  
  218.     ymid=(parentPt[1]-cntrPt[1])/2.0+cntrPt[1]  
  219.     createPlot.ax1.text(xmid,ymid,txtString)  
  220.   
     
  221. #绘制节点以及箭头  
  222. def plotNode(nodeTxt,centerPt,parentPt,nodeType):  
  223.     createPlot.ax1.annotate(nodeTxt,xy=parentPt,xycoords='axes fraction',  
  224.         xytext=centerPt,textcoords='axes fraction',  
  225.         va='center',ha='center',bbox=nodeType,  
  226.         arrowprops=arrow_args)  
  227.   
     
  228. ''''' 
  229. ------------------------- 
  230. 储存决策树，使用pickle，序列化存储 
  231. ------------------------- 
  232. '''  
  233. import pickle  
  234. def storeTree(inputTree,filename):  
  235.     with open(filename,'wb') as fw:  
  236.         pickle.dump(inputTree,fw)  
  237.   
     
  238. def loadTree(filename):  
  239.     with open(filename,'rb') as fr:  
  240.         return pickle.load(fr)  
  241.   
     
  242. if __name__=='__main__':  
  243.     fr=open('lenses.txt')  
  244.     lenses=[inst.strip().split('\t') for inst in fr.readlines()]  
  245.     lensesLabels=['age','prescript','astigmatic','tearRate']  
  246.     lensesTree=createTree(lenses,lensesLabels)  
  247.     createPlot(lensesTree)  
  248.     storeTree(lensesTree,'lensesTree-syt.txt')  

机器学习实战 -- 决策树(ID3)的更多相关文章

  1. [机器学习实战] 决策树ID3算法

    1. 决策树特点: 1)优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据. 2)缺点:可能会产生过度匹配问题. 3)适用数据类型:数值型和标称型. 2. 一般流程: ...

  2. 机器学习之决策树(ID3)算法与Python实现

    机器学习之决策树(ID3)算法与Python实现 机器学习中,决策树是一个预测模型:他代表的是对象属性与对象值之间的一种映射关系.树中每个节点表示某个对象,而每个分叉路径则代表的某个可能的属性值,而每 ...

  3. 机器学习实战---决策树CART回归树实现

    机器学习实战---决策树CART简介及分类树实现 一:对比分类树 CART回归树和CART分类树的建立算法大部分是类似的,所以这里我们只讨论CART回归树和CART分类树的建立算法不同的地方.首先,我 ...

  4. [机器学习&数据挖掘]机器学习实战决策树plotTree函数完全解析

    在看机器学习实战时候,到第三章的对决策树画图的时候,有一段递归函数怎么都看不懂,因为以后想选这个方向为自己的职业导向,抱着精看的态度,对这本树进行地毯式扫描,所以就没跳过,一直卡了一天多,才差不多搞懂 ...

  5. 《机器学习实战》ID3算法实现

    注释:之前从未接触过决策树,直接上手对着书看源码,有点难,确实有点难-- 本代码是基于ID3编写,之后的ID4.5和CART等还没学习到 一.决策树的原理 没有看网上原理,直接看源码懂得原理,下面是我 ...

  6. 机器学习实战---决策树CART简介及分类树实现

    https://blog.csdn.net/weixin_43383558/article/details/84303339?utm_medium=distribute.pc_relevant_t0. ...

  7. 决策树ID3算法python实现 -- 《机器学习实战》

    from math import log import numpy as np import matplotlib.pyplot as plt import operator #计算给定数据集的香农熵 ...

  8. 机器学习之决策树（ID3 、C4.5算法）

    声明:本篇博文是学习<机器学习实战>一书的方式路程,系原创,若转载请标明来源. 1 决策树的基础概念 决策树分为分类树和回归树两种,分类树对离散变量做决策树 ,回归树对连续变量做决策树.决 ...

  9. 机器学习之决策树一-ID3原理与代码实现

    决策树之系列一ID3原理与代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9429257.html 应用实 ...

随机推荐

  1. 基于vue-cli 将webpack3 升级到 webpack4 配置

       升级webpack4前 先删除之前的webpack, babel-loader  下载 webpack npm i -D webpack@4 webpack-cli@3 webpack-dev- ...

  2. 在 CentOS7 上安装 swftools

    1.从官网下载 swftools,这里下载的是 0.9.2 版本: wget http://www.swftools.org/swftools-0.9.2.tar.gz 2.下载后得到 swftool ...

  3. django 定制admin

    https://www.cnblogs.com/liwenzhou/p/9519321.html

  4. traffic_light_bag_file 数据集 下载链接

    链接:https://pan.baidu.com/s/19p5aGRfs6iFtN_SWAxCkRQ 密码:v9wx

  5. python web应用--WSGI接口（二）

    WSGI接口定义非常简单,它只要求Web开发者实现一个函数,就可以响应HTTP请求.我们来看一个最简单的Web版本的“Hello, web!”: 1 # server.py 2 # 从wsgiref模 ...

  6. 2018.8.19 mybatis 环境搭建---配置mysql 。（Windows环境下面）

    安装mysql Install/Remove of the Service Denied!错误的解决办法 在windos 的cmd下安装mysql 在mysql的bin目录下面执行: mysqld - ...

  7. c# base new 等关键字基础

    base关键字 不仅可以  调用父类的 实例方法,也能狗调用父类的 构造方法 https://www.cnblogs.com/aehyok/p/3519599.html

  8. IOError: [Errno 22] invalid mode ('rb') or filename: 'C

    dataset = scipy.io.loadmat('F:\test_data.mat') 报错 IOError: [Errno ] invalid mode ('rb') or filename: ...

  9. Python中的__name__和__main__含义详解

    1背景 在写Python代码和看Python代码时,我们常常可以看到这样的代码: ? 1 2 3 4 5 def main():     ......   if __name == "__m ...

  10. caffe中各种cblas的函数使用总结

    转来的,来自:http://www.cnblogs.com/huashiyiqike/p/3886670.html 总结的很赞,转到这里,留一下笔记.感觉cblas的函数名字很好记的,试着去找过源代码 ...