可参见这两个页面：

1. http://www.culatools.com/dense/lapack/

2. http://www.netlib.org/lapack/lug/node1.html

根据实际需要，找到相应的程序，再去lapack中搜索该程序的源码来调用即可。

以求解超定线性方程组为例，它采用最小二乘法（Least Squares Routines）求解，使 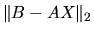最小，相应的程序有：

Table 2.3: Driver routines for linear least squares problems
Operation Single precision Double precision
  real complex real complex
solve LLS using QR or LQ factorization SGELS CGELS DGELS ZGELS
solve LLS using complete orthogonal factorization SGELSY CGELSY DGELSY ZGELSY
solve LLS using SVD SGELSS CGELSS DGELSS ZGELSS
solve LLS using divide-and-conquer SVD SGELSD CGELSD DGELSD ZGELSD

Lapack求解线性方程组的更多相关文章

  1. matlab 求解线性方程组之LU分解

    线性代数中的一个核心思想就是矩阵分解,既将一个复杂的矩阵分解为更简单的矩阵的乘积.常见的有如下分解: LU分解:A=LU,A是m×n矩阵,L是m×m下三角矩阵,U是m×n阶梯形矩阵 QR分解: 秩分解 ...

  2. 【原创】开源Math.NET基础数学类库使用(06)直接求解线性方程组

                   本博客所有文章分类的总目录:[总目录]本博客博文总目录-实时更新  开源Math.NET基础数学类库使用总目录:[目录]开源Math.NET基础数学类库使用总目录 前言 ...

  3. python 求解线性方程组

    Python线性方程组求解 求解线性方程组比较简单,只需要用到一个函数(scipy.linalg.solve)就可以了.比如我们要求以下方程的解,这是一个非齐次线性方程组: 3x_1 + x_2 - ...

  4. Numpy库进阶教程（一）求解线性方程组

    前言 Numpy是一个很强大的python科学计算库.为了机器学习的须要.想深入研究一下Numpy库的使用方法.用这个系列的博客.记录下我的学习过程. 系列: Numpy库进阶教程(二) 正在持续更新 ...

  5. matlab中求解线性方程组的rref函数

    摘自:http://www.maybe520.net/blog/987/ matlab中怎么求解线性方程组呢? matlab中求解线性方程组可应用克拉默法则(Cramer's Rule)即通过det( ...

  6. [Matlab]求解线性方程组

    转自:http://silencethinking.blog.163.com/blog/static/911490562008928105813169/ AX=B或XA=B在MATLAB中,求解线性方 ...

  7. Numpy计算逆矩阵求解线性方程组

    对于这样的线性方程组: x + y + z = 6 2y + 5z = -4 2x + 5y - z = 27 可以表示成矩阵的形式: 用公式可以表示为:Ax=b,其中A是矩阵,x和b都是列向量 逆矩 ...

  8. Numpy求解线性方程组

    Numpy求解线性方程组 对于Ax=b,已知A和b,怎么算出x? 1. 引入包 2. 求解 验证

  9. JAVA求解线性方程组-列主元高斯消去法

    package MyMath; import java.util.Scanner; public class Gauss { /** * @列主元高斯消去法 */ static double x[]; ...

随机推荐

  1. WebStorm过期解决方法

    第一步:先删除C:\Users\本机用户名\.WebStorm2016.3\config文件中eval文件. 第二步:打开webstrom 如图,填写许可证激活码:http://idea.imsxm. ...

  2. iis相关概念和操作

    iis相关 iis是什么?      它是互联网信息服务的缩写,是网页服务组件(即多种服务器集成) iis为什么存在,作用是什么?      方便于网络上发布信息. 如何使用等等? 1)打开win7的 ...

  3. php高精度计算问题

    从事金融行业,资金运算频繁,这里说下我遇到的坑....稍不留神,用户资金可能损失几十万,甚至更可怕......直接上实例吧: javascript 0.1 + 0.2 为啥不等于 0.3 ? (正确结 ...

  4. Oracle基础知识点——Oracle服务端和客户端

    Oracle服务端 服务端提供oracle服务的实例,其是数据库的核心,用于数据库的管理,对象的管理与存储.数据的存储.查询.数据库资源的监控.监听等一些服务. 例子:比如一台机子上安装了Oracle ...

  5. SSM学习（一）Mybatis

    Mybatis Notes Mybatis First 创建Maven项目 配置依赖 <dependencies> <dependency> <groupId>ju ...

  6. Linux SSH 基于密钥交换的自动登录原理简介及配置说明

    协商交互过程 1.客户端向目标服务器发送登录请求.在SSH 服务启用了证书验证登录方式后,会优先通过证书验证方式进行登录验证. 2.目标服务器根据 SSH 服务配置,在用户对应目录及文件中读取到有效的 ...

  7. LintCode 846.多关键字排序

    LintCode 846.多关键字排序 描述 给定 n 个学生的学号(从 1 到 n 编号)以及他们的考试成绩,表示为(学号,考试成绩),请将这些学生按考试成绩降序排序,若考试成绩相同,则按学号升序排 ...

  8. c#操作json的两种方式

    总结一下C#操作json的两种方式,都是将对象和json格式相转. 1.JavaScriptSerializer,继承自System.Web.Script.Serialization private ...

  9. C++第三章复习与总结（思维导图分享）

    在完成了第三章的学习后,为了便于日后的复习整理,我制作了一张思维导图,有需要的可以自取. 函数的定义与使用 带默认值的函数 在C++中我们可以为函数添加默认的参数值,在调用时可不传入或部分传入参数,为 ...

  10. Jenkins去GitLab拉取Java代码自动打包

    jenkins的部署 一.部署git 1)先检查系统是否已经自带了git,如果有,就卸载 $ rpm -qa | grep git && rpm -e git --nodeps 2)开 ...