计算几何-凸包-toleft test

toLeftTest

toLeftTest是判断一个点是否在有向直线左侧的算法。

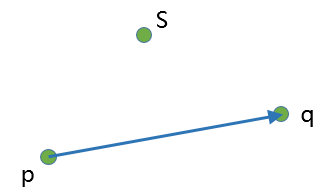
当点s位于向量pq左侧时，toLeftTest返回true。当点s位于向量pq右侧时，toLeftTest返回false。

具体的算法可以根据三角形的有符号面积来计算

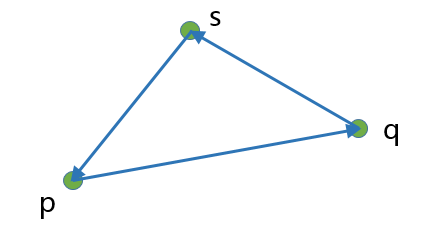
对应上图中的 2倍三角形面积area 的公式为

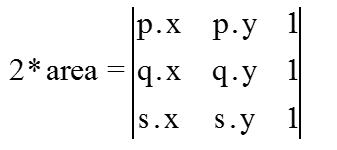
当pqs的方向为逆时针时，面积area为正；当pqs的方向为顺时针时，面积area为负值。当area为0时，说明点s在直线pq上

下面的算法有效避免了除法的出现，减少了计算误差。

 bool toLeftTest(Point p, Point q, Point s){
     return area2(p,q,s) > ;
 }

 int area2(Point p, Point q, Point s){
     return
         p.x * q.y - p.y * q.x
       + q.x * s.y - q.y * s.x
       + s.x * p.y - s.y * p.x;
 }

应用：

1. 需要考察角度的最大最小值时

InTriangleTest

InTriangleTest用于判断一个点是否在给点的三角形内。

三角形的三条边所在直线将平面分成了7份，无论三角形三个顶点是逆时针还是顺时针的，位于三角形内的点对三边向量所做的toLeftTest结果都相同。

方法一：利用toLeftTest

 bool inTriangleTest(Point r, Point p, Point q, Point s){
     int a = toLeftTest(p,q,r);
     int b = toLeftTest(q,s,r);
     int c = toLeftTest(s,p,r);
     return ( a ==  b && b == c);
 }

凸包的toLeftTest性质

给定一个逆时针的凸包，在平面上随意取一个点P。对于凸包上的点Q，以PQ为向量，对Q先前邻接的点Q-1和之后邻接的点Q+1做 toLeftTest测试。

1. 当点P在凸包内时

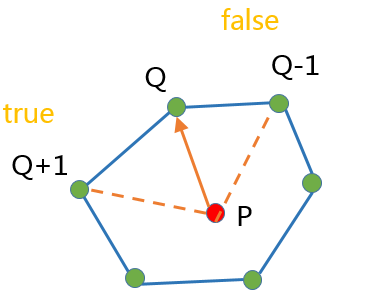
对于凸包上任意的点Q，Q先前邻接的点Q-1和之后邻接的点Q+1的 toLeftTest 结果分别为false和true，记为 FT。

1. 当点P在凸包外时

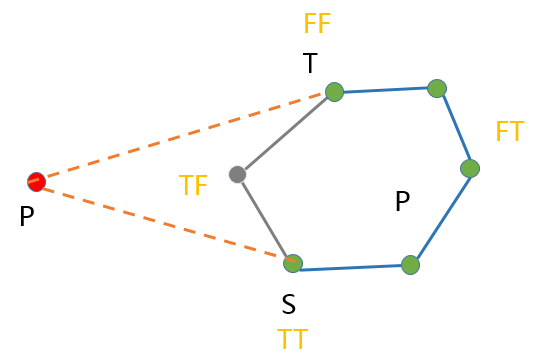
通过P可以在凸包上找到两个点T和S，向量PS和PT会与凸包相切。

2.1 点T和点S的前驱和后继点（T-1和T+1，S-1和S+1）的toLeftTest结果均为两个相同的值，要么都为true，要么都为false。记为 TT 和 FF。
2.2 凸包TS之间的点（TS具有方向性），其前驱和后继的toLeftTest测试结果为true，false。 记为 TF。
2.3 凸包ST之间的点（ST具有方向性），其前驱和后继的toLeftTest测试结果为false，true。 记为 FT。

inConvexPolygonTest

inConvexPolygonTest是用来判断一个点是否在一个凸包多边形的内部。下面的算法要求输入的凸包点集是逆时针的。过程可看下图

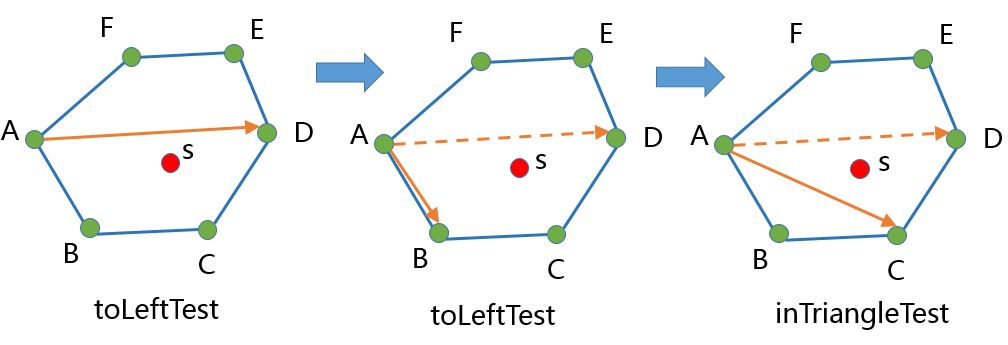
算法的过程是需要将 inConvexPolygonTest 最终转化为 inTriangleTest。取凸包的第一个点作为InTriangleTest的三角形的一个点，通过二分找到中间点，然后通过不断的inLeftTest和二分, 从而找到将判断点夹在中间的三角形，最后进行inTriangleTest，用inTriangleTest的结果作为inConvexPolygonTest的结果。

以上面的图作为inConvexPolygonTest算法的过程例子

1. 取凸包的第一个点A和中间的点D。
2. 用向量AD对点s进行toLeftTest。 toLeftTest(A,D,s)
3. 上一步toLeftTest结果为false, 所以对右侧的点进行二分找到点B。
4. 用向量AB对点s进行toLeftTest。 toLeftTest(A,B,s)
5. 上一步toLeftTest结果为true, 所以对左侧的点进行二分找到点C。
6. 用向量AC对点s进行toLeftTest。 toLeftTest(A,C,s)
7. 由于toLeftTest(A,C,s)返回true,且D邻接在点C的左侧，所以确定进行inTriangleTest的为三角形 ACD。
8. 用三角形ACD对点s进行inTriangleTest，返回true，所以点s在凸包内。

inPolygonTest

左右两个不相交凸包的两条公切线求法

graham scan 以O(nlogn)复杂度求平面点集的凸包

算法步骤为

1. 找到 lowest then leftmost的点A（在笛卡尔坐标系中，y值最小的点。如果y值相同，则要求x值最小。）
2. 以点A建立极角坐标系，对剩余的点以极角的大小进行从小到大排序，找出极角最小的点B。
3. 建立堆栈S，将点A压栈，将点B压栈。
4. 遍历剩余的点，记正在遍历的点为P。以堆栈S的次栈顶的点Q（最开始时为A点），栈顶的点R（最开始时为点B）,和点P进行toLeftTest测试。
   4.1 如果toLeftTest测试结果为true，将点T压进堆栈S。
   4.2 如果toLeftTest测试结果为false
   4.2.1 如果堆栈S中的点的个数小于等于3，不做任何事情。
   4.2.2 如果堆栈S中点的个数大于3，将堆栈S中的栈顶的点推出（pop），然后返回到步骤4继续做toLeftTest测试。
5. 直到遍历完所有的点。

算法结束后，堆栈S中从栈底到栈顶的点集及为凸包逆时针方向的点集。

Common tangle 左右两个子凸包的公切线

Geometry Interaction （线段相交）

Segments Interaction（线段集的求交）

线段集的求交是给定 线段的集合作为输入 求出这些 线段中的所有可能交点

一种与输出的交点数敏感的算法是平面扫描算法。以一条扫描线扫过所有的线段集，以线段集中的所有起点、终点、和将来求出的交点作为所有事件点，当扫描线经过事件点时，则需要对与扫描线相交的线段中的部分线段进行相交检测，判断从而判断是否存在交点。

1. 当扫描线经过一条线段的起点，即事件点为线段的起点。将线段放入与扫描线相交的线段的有序集合中，并与其前驱和后继的线段进行相交检测。
   1.1 如果有交点，记录交点。并把交点纳入事件点。
   1.2 如果没有交点，继续扫描，进入下一个事件点。
2. 当事件点为交点。将交点的两条线段在与扫描线相交的线段的有序集合中交换顺序，并与其新前驱或新后继的线段进行相交检测。
   2.1 如果有交点，记录交点。并把交点纳入事件点。
   2.2 如果没有交点，继续扫描，进入下一个事件点。
3. 当事件点为线段的终点。将该线段从与扫描线相交的线段的有序集合中移除，并对其移除之前的前驱和后继线段进行相交检测。
   3.1 如果有交点，记录交点。并把交点纳入事件点。
   3.2 如果没有交点，继续扫描，进入下一个事件点。

isTwoConvexPolygonIntersected

参考资料

学堂在线 清华大学 邓俊辉的 计算几何 课程+https://www.cnblogs.com/smallpi/p/7257762.html