BestCoder6 1002 Goffi and Squary Partition(hdu 4982) 解题报告

题目链接：http://bestcoder.hdu.edu.cn/contests/contest_showproblem.php?pid=1002&cid=530

（格式有一点点问题，直接粘下来吧）

题目意思：给出 n 和 k，问能否构造 k-1个不同的数使得这 k-1 个数（每个数都为正整数）的和等于一个数的平方，且 k 个数（都为正整数）的和等于 n。

错了差不多十多次，终于要看别人思路了.......

为了将问题简化，且保证 k-1 个数都是不同的，我们从自然数1，2，...，k-2 构造出前 k-2 个数，看清楚，不是 k-1 而是 k-2。因为最后第 k-1 个数有待斟酌！！！

设 square 为 k-1 个数之和，也就是等于的某个数的平方啦，remain 就是 n - square了。

先排除两种特殊情况：

（1） remain = 0 （不符合正整数的要求）或者 (k-1) * k /2 > square（因为是从1开始构造的，最小的square 都需要大于等于 (k-1）* k /2（1+2+3+...+k-1) ，避免无谓的计算

　　（2）如果square = 1 并且 remain = 1 ，那么无解。这就是Sample 中的2 2了。

然后开始构造k-2个数。构造的时候，如果遇到remain（假如为x），就跳过一位，变成x+1，使得构造的数中不包含remain。因此代码中就有 x 多自增1次的操作了。

构造完 k-2 个数之后（设和为sum），我们要对最后一个数，即第 k-1个数进行讨论（代码中的need，它的值等于 n - sum - remain）。如果这个 need <= x (第 k-2 个数的值就是x)，代表 k - 1个数中有两个数是相同的，与题意不符。而且它就算怎样调整都不能构造出答案，因为我们是从最小的自然数1开始构造的！

比较难理解的是，最后的那个k-1的数，我们还是x++，但是sum + x 有可能并不等于 （确切来讲是小于，如果是大于都是无解的，从最小数开始构造嘛）square，但是我们可以调整 k-2个数中的某个数ai令它大点--->ai+k，使得sum + x（此时的x不是原来单纯的 x++ 了，x = square-(sum-ai+ai+k）） 不过这些情况比较复杂，所以我们反其道而行之，讨论无解的情况！

无解的时候，有两种情况。最后 前面不是说 x++ 吗，那么第一种肯定无解的情况：x == remain && need == remain！这个表示remain 在k-2个数的构造中根本没有遇到。而且need这个值 是必须的，无论前面怎样调整，还是那个道理，从最小数1开始构造。

最难理解的是第二种情况 x+1 == remain && need == remain （我也想了好久才想通，wa了这么多次就是这个没想出来）。remain 是动不了的，只能从need 和 前面已经构造了的 k-2个数中开刀。

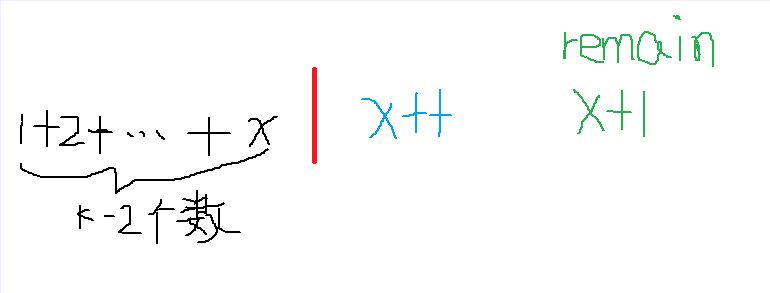
我们不希望need = remain，于是只能让k-2个数中的某个数增加1（确切来讲只能是黑色字体的x，因为数与数之间是紧挨着的），变成蓝色部分的x++，此时need 确实不等于 remain，但是need 却等于蓝色部分的x++（need - 1）了，也就是最后构造出来的k-1 个数中有两个数是相同的！！！

只要排除这两种情况，就表示可以得出解。

 #include <iostream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 using namespace std;

 int n, k;

 bool check(int square, int remain)
 {
     if (remain ==  && square == )  // k = 2, remain = 1的情况
         return false;
     int sum = ;
     int x = ;
     for (int i = ; i < k-; i++)  // 构造k-2个数
     {
         x++;
         if (x == remain)
             x++;
         sum += x;
     }
     int need = n-sum-remain;
     if (need <= x)    // 最后第k-1个数在前k-2个已构造数里面
         return false;
     // need > x(未自增前)，有可能与remain有冲突(remain在k-2个数之外)
     x++;
     if (x == remain || x +  == remain)
     {
         if (need == remain)  // need == remain == x
           return false;   // or need == remain == x+1
     }
     return true;  // need > x+1
 }

 int main()
 {
     while (scanf("%d%d", &n, &k) != EOF)
     {
         int flag = ;
         for (int i = ; i * i < n && !flag; i++)
         {
             int square = i*i;
             int remain = n - square;
             if (remain ==  || (k-)*k/ > square)
                 continue;
             if (check(square, remain))
             {
                 flag = ;
                 break;
             }
         }
         printf("%s\n", flag ? "YES" : "NO");
     }
     return ;
 }