Leetcode之广度优先搜索（BFS）专题-1162. 地图分析（As Far from Land as Possible）

Leetcode之广度优先搜索（BFS）专题-1162. 地图分析（As Far from Land as Possible）

BFS入门详解：Leetcode之广度优先搜索（BFS）专题-429. N叉树的层序遍历（N-ary Tree Level Order Traversal）

---

你现在手里有一份大小为 N x N 的『地图』（网格） grid，上面的每个『区域』（单元格）都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地，你知道距离陆地区域最远的海洋区域是是哪一个吗？请返回该海洋区域到离它最近的陆地区域的距离。

我们这里说的距离是『曼哈顿距离』（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。

如果我们的地图上只有陆地或者海洋，请返回 -1。

示例 1：

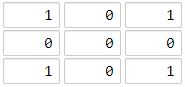
输入：[[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释：
海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大，最大距离为 2。

示例 2：

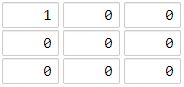
输入：[[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释：
海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大，最大距离为 4。

提示：

1. 1 <= grid.length == grid[0].length <= 100
2. grid[i][j] 不是 0 就是 1

---

给一个地图，上面有1和0，求离1最远的0的曼哈顿长度。

我们换个思路，用BFS。

1、先把所有1进队列

2、把1取出来，向周围的0扩散，把周围的0变成1，距离+1

形象一点就是一层一层把整个图全部填成1，最后得到一个全是1的图，我们就可以知道最长的距离了。

AC代码：

class Solution {
    int dirx[] = {1,-1,0,0};
    int diry[] = {0,0,1,-1};
    public int maxDistance(int[][] grid) {
        int ans = 0;
        Queue<int[]> queue = new LinkedList<>();
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if(grid[i][j]==1)
                    queue.offer(new int[]{i,j,0});
            }
        }
        if(queue.isEmpty() || queue.size()==grid.length*grid[0].length){
            return -1;
        }
        while (!queue.isEmpty()){
            int[] temp = queue.poll();
            int x = temp[0];
            int y = temp[1];
            int step = temp[2];
            ans = Math.max(ans,step);
            for (int i = 0; i < 4; i++) {
                int xx = x + dirx[i];
                int yy = y + diry[i];
                if(xx>=0 && xx<grid.length && yy>=0 && yy<grid[0].length && grid[xx][yy]==0){
                    grid[xx][yy] = 1;
                    queue.offer(new int[]{xx,yy,step+1});
                }
            }
        }
        return ans;
    }
}