中国剩余定理（crt）和扩展中国剩余定理（excrt）

数论守门员二号 =。=

中国剩余定理：

1.一次同余方程组：

一次同余方程组是指形如x≡ai(mod mi) (i=1，2，…，k)的同余方程构成的组

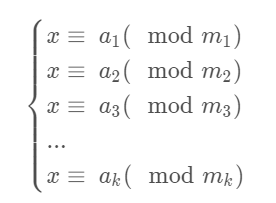
中国剩余定理的主要用途是解一次同余方程组，其中m1,m2,...,mk互质

2.中国剩余定理：

令M=m1*m2*...*mk（即所有m的lcm）
ti为同余方程M/mi*ti≡1(mod mi)的最小正整数解

则存在解x=∑ai*M/mi*ti

通解为x+i*M

最小非负整数解为(x%M+M)%M

（我承认这段是抄的orz

原文看起来更方便：https://blog.csdn.net/niiick/article/details/80229217）

M/mi*ti≡1(mod mi)可转化为M/mi*ti+mi*y=1，然后用exgcd求ti

其中gcd(M/mi, mi)=1，意义为方程组一定有解

3.证明：

对于第k个方程

①当i≠k时，有mk|M/mi，即ai*M/mi*ti≡0(mod mk)

②当i=k时，有M/mk*tk≡1(mod mk)，即ak*M/mk*tk≡ak(mod mk)

故∑ai*M/mi*ti≡ak(mod mk)

4.代码：

（其中LL是long long，qcm是快速乘）

 LL crt(){
     LL bwl=;
     for(int i=;i<=k;++i){
         LL x,y;
         exgcd(M/m[i],m[i],x,y);
         if(x<)  x=x%m[i]+m[i];
         bwl=(bwl+qcm(qcm(a[i],M/m[i]),x))%M;
     }
     return (bwl+M)%M;
 }

5.孙子算经：
《孙子算经》：今有物不知其数，三三数之剩二；五五数之剩三；七七数之剩二。问物几何？

《算法统宗》：三人同行七十稀，五树梅花廿一枝，七子团圆月正半，除百零五便得知。

其中70=3*5*2，70%3=1，21=3*7*1，21%5=1，15（半个月）=3*5*1，15%7=1

用70*2+21*3+15*2=233除3*5*7=105，得到的余数23即为答案

70=3*5*2，21=3*7*1，15=3*5*1三式中的最后一个乘数2、1、1即为上文提到的di

数字还挺吉利的233

扩展中国剩余定理：

1.一次同余方程组：

扩展中国剩余定理的主要用途是解一次同余方程组，其中m1,m2,...,mn不一定互质

2.扩展中国剩余定理：

令前k-1个方程组成的同余方程组的一个解为x

且M为前k-1个模数的lcm

则前k-1个方程的方程组的通解为x+i*M

现在将第k个方程加入

只需求一个正整数t，使得

x+t*M≡ak(mod mk)

可以转化为M*t+mk*y=ak-x

然后用exgcd求出t

若此方程无解，则整个同余方程组无解

否则x+t*M为前k个方程的方程组的一个解

（这段也是我抄的，原文和上边一样orz）

3.代码：

（其中LL是long long，qcm是快速乘，三个参数分别为两个乘数和模数）

 LL excrt(){
     LL M=m[],ans=a[];
     for(int i=;i<=k;++i){
         LL x,y;
         LL d=gcd(M,m[i]);
         LL c=(a[i]-ans%m[i]+m[i])%m[i];
         if(c%d)  return -;
         exgcd(M,m[i],x,y);
         x=qcm(x,c/d,m[i]/d);
         ans+=qcm(x,M,M*m[i]);
         M*=m[i]/d;
         ans=(ans%M+M)%M;
     }
     return ans;
 }

4.细节：

1.有些题数字卡得严，必须要用快速乘

2.快速乘时注意第二个乘数必须为正，要用通解处理

3.每次快速乘的模数不一定一样，需要好好考虑

例题：

洛谷3868 猜数字

洛谷4777 扩展中国剩余定理