[BZOJ1116]CLO[并查集]

看了样例突然发现= =无向边不会增加入度。

然后发现是环套环。

一个环所有点入度都为2。

最后的图无视所有无向边的话大概是这样的(将就一下

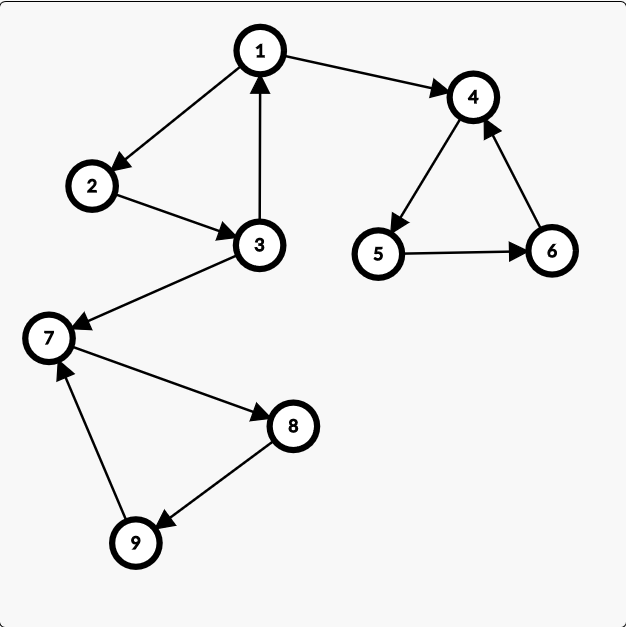
然后就可以并查集维护一下联通性...

当x , y属于一个联通块（假设是一条链），那么这条链中的每一个点都能作为根节点$root$。因为n个节点的链n-1条边只有root是入度为0的。

否则，对合并后的块(假设y所在的块并入x所在的块)，对x的块打标机。

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 inline ll _() {
     ll x=,f=; char ch=getchar();
     for(;ch<''||ch>'';ch=getchar())
         if(ch=='-')f=-f;
     for(;ch>=''&&ch<='';ch=getchar())
         x=x*+ch-'';
     return x*f;
 }
 #define _ _()
 const int N=1e5+;
 int f[N],vis[N];
 inline int find( int x ) { return f[x]==x?x:f[x]=find(f[x]); }
 int main() {
     int n=_,m=_;
     for(int i=;i<=n;i++) f[i]=i,vis[i]=;
     for(int i=,x,y;i<=m;i++) {
         x=find(_); y=find(_);
         if(x==y) vis[x]=;
         else { f[y]=x; vis[x]=vis[x]|vis[y]; }
     }
     for(int i=;i<=n;i++) if(!vis[find(i)]) return puts("NIE"),;
     puts("TAK");
 }