(原创)Stanford Machine Learning (by Andrew NG) --- (week 3) Logistic Regression & Regularization
coursera上面Andrew NG的Machine learning课程地址为:https://www.coursera.org/course/ml
我曾经使用Logistic Regression方法进行ctr的预测工作,因为当时主要使用的是成型的工具,对该算法本身并没有什么比较深入的认识,不过可以客观的感受到Logistic Regression的商用价值。
Logistic Regression Model
A. objective function
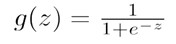 其中z的定义域是(-INF,+INF),值域是[0,1]
其中z的定义域是(-INF,+INF),值域是[0,1]

We call this function sigmoid function or logistic function.
We want 0 ≤ hθ(x) ≤ 1 and hθ(x) = g(θTx) 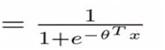
B. Decision boundary
在 0 ≤ hθ(x) ≤ 1的连续空间内,用logistic regression做分类时,我们可以将hθ(x)等于0.5作为分割点。
- if hθ(x) ≥ 0.5,predict "y = 1";
- if hθ(x) < 0.5,predict "y = 0";
而Decision Boundary就是能够将所有数据点进行很好地分类的 h(x) 边界。
C. Cost Function
Defination:
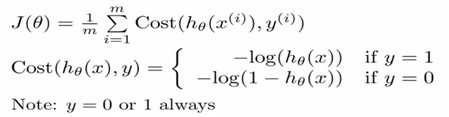
Because y = 0 or y = 1,and cost function can been writen as below:
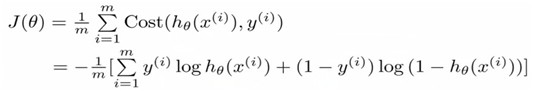
Advanced optimization
In order to minimize J(θ), and get θ. Then how to get minθ J(θ) ?
A. Using gradient descent to do optimization
Repeat{
} 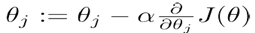
Compute 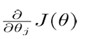 , we can get (推导过程下方附录)
, we can get (推导过程下方附录)
Repeat{
}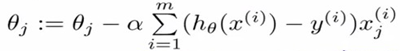
B.其他基于梯度的优化方法
- Conjugate gradient(共轭梯度)
- 牛顿法
- 拟牛顿法
- BFGS(以其发明者Broyden, Fletcher, Goldfarb和Shanno的姓氏首字母命名),公式:
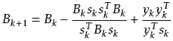
- L-BFGS
- OWLQN
Multi classification
How to do multi classification using logistic regression? (one vs rest)
A. How to train model?
当训练语料标注的类别大于2时,记为n。我们可以训练n个LR模型,每个模型的训练数据正例是第i类的样本,反例是剩余样本。(1≤ i ≤n)
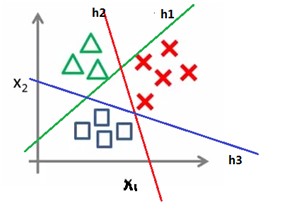
B.How to do prediction?
在 n 个 hθ(x) 中,获得最大 hθ(x) 的类就是x所分到的类,即 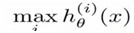
Overfitting
A. How to address overfitting?
a) Reduce number of features.
- Manually select which features to keep.
- Model selection algorithm (later in course).
b) Regularization(规范化)
- Keep all the features, but reduce magnitude/values of all parameters .
- Works well when we have a lot of features, each of which contributes a bit to predicting .
c) Cross-validation(交叉验证)
- Holdout验证: 我们将语料库分成:训练集,验证集和测试集;
- K-fold cross-validation:优势在于同时重复运用随机产生的子样本进行训练和验证,每次的结果验证一次;
B. Regularized linear regression
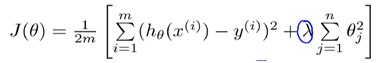
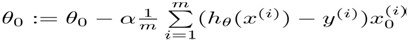 (式1)
(式1)
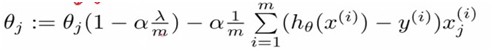 (式2)
(式2)
C. Normal equation
Non-invertibility(optional/advanced).
suppose m ≤ n m: the number of examples; n: the number of features;
θ = (XTX)-1XTy
由(式1)和(式2)可以得到对应的n+1维参数矩阵。
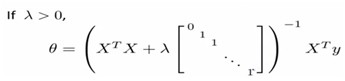
D. Regularized logistic regression
Regularized cost function:
J(θ) = 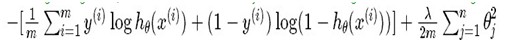
Gradient descent:
Repeat{
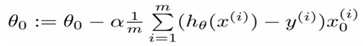
} 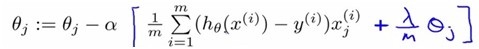
Logistic Regression与Linear Regression的关系
Logistic Regression是线性回归的一种,Logistic Regression 就是一个被logistic方程归一化后的线性回归。
Logistic Regression的适用性
- 可用于概率预测,也可用于分类;
- 仅能用于线性问题;
- 各feature之间不需要满足条件独立假设,但各个feature的贡献是独立计算的。
HOMEWORK
好了,既然看完了视频课程,就来做一下作业吧,下面是Logistic Regression部分作业的核心代码:
1.sigmoid.m
m = 0;
n=0;
[m,n] = size(z);
for i = 1:m
for j = 1:n
g(i,j) = 1/(1+e^(-z(i,j)));
end
end
2.costFunction.m
for i =1:m
J = J+(-y(i)*log(sigmoid(X(i,:)*theta)))-(1-y(i))*log(1-sigmoid(X(i,:)*theta));
end
J=J/m;
for j=1:size(theta)
for i=1:m
grad(j)=grad(j)+(sigmoid(X(i,:)*theta)-y(i))*X(i,j);
end
grad(j)=grad(j)/m;
end
3.predict.m
for i=1:m
if(sigmoid(theta'*X(i,:)')>0.5)
p(i)=1;
else
p(i)=0;
endif
end
4.costFunctionReg.m
for i =1:m
J = J+(-y(i)*log(sigmoid(X(i,:)*theta)))-(1-y(i))*log(1-sigmoid(X(i,:)*theta));
end
J=J/m;
for j=2:size(theta)
J = J+(lambda*(theta(j)^2)/(2*m));
end for j=1:size(theta)
for i=1:m
grad(j)=grad(j)+(sigmoid(X(i,:)*theta)-y(i))*X(i,j);
end
grad(j)=grad(j)/m;
end
for j=2:size(theta)
grad(j)=grad(j)+(lambda*theta(j))/m;
end
附录
Logistic regression gradient descent 推导过程

(原创)Stanford Machine Learning (by Andrew NG) --- (week 3) Logistic Regression & Regularization的更多相关文章
- (原创)Stanford Machine Learning (by Andrew NG) --- (week 1) Linear Regression
Andrew NG的Machine learning课程地址为:https://www.coursera.org/course/ml 在Linear Regression部分出现了一些新的名词,这些名 ...
- (原创)Stanford Machine Learning (by Andrew NG) --- (week 10) Large Scale Machine Learning & Application Example
本栏目来源于Andrew NG老师讲解的Machine Learning课程,主要介绍大规模机器学习以及其应用.包括随机梯度下降法.维批量梯度下降法.梯度下降法的收敛.在线学习.map reduce以 ...
- (原创)Stanford Machine Learning (by Andrew NG) --- (week 8) Clustering & Dimensionality Reduction
本周主要介绍了聚类算法和特征降维方法,聚类算法包括K-means的相关概念.优化目标.聚类中心等内容:特征降维包括降维的缘由.算法描述.压缩重建等内容.coursera上面Andrew NG的Mach ...
- (原创)Stanford Machine Learning (by Andrew NG) --- (week 7) Support Vector Machines
本栏目内容来源于Andrew NG老师讲解的SVM部分,包括SVM的优化目标.最大判定边界.核函数.SVM使用方法.多分类问题等,Machine learning课程地址为:https://www.c ...
- (原创)Stanford Machine Learning (by Andrew NG) --- (week 9) Anomaly Detection&Recommender Systems
这部分内容来源于Andrew NG老师讲解的 machine learning课程,包括异常检测算法以及推荐系统设计.异常检测是一个非监督学习算法,用于发现系统中的异常数据.推荐系统在生活中也是随处可 ...
- (原创)Stanford Machine Learning (by Andrew NG) --- (week 4) Neural Networks Representation
Andrew NG的Machine learning课程地址为:https://www.coursera.org/course/ml 神经网络一直被认为是比较难懂的问题,NG将神经网络部分的课程分为了 ...
- (原创)Stanford Machine Learning (by Andrew NG) --- (week 1) Introduction
最近学习了coursera上面Andrew NG的Machine learning课程,课程地址为:https://www.coursera.org/course/ml 在Introduction部分 ...
- (原创)Stanford Machine Learning (by Andrew NG) --- (week 5) Neural Networks Learning
本栏目内容来自Andrew NG老师的公开课:https://class.coursera.org/ml/class/index 一般而言, 人工神经网络与经典计算方法相比并非优越, 只有当常规方法解 ...
- (原创)Stanford Machine Learning (by Andrew NG) --- (week 6) Advice for Applying Machine Learning & Machine Learning System Design
(1) Advice for applying machine learning Deciding what to try next 现在我们已学习了线性回归.逻辑回归.神经网络等机器学习算法,接下来 ...
随机推荐
- zuul进行rate limit
maven <dependency> <groupId>com.marcosbarbero.cloud</groupId> <artifactId>sp ...
- SD 模拟sip 读写子程序
void simulate_spi_write_byte(u8 data){ u8 kk; SPI3_CS(0); SPI3_SCK(0); delay_us(1); //???spi???1/2us ...
- 64_l4
libnormaliz-devel-3.1.4-2.fc26.i686.rpm 23-May-2017 00:24 31214 libnormaliz-devel-3.1.4-2.fc26.x86_6 ...
- ogre3d环境配置 SDK安装配置及简单事例教程
ogre3d环境配置 SDK安装配置及简单事例教程 http://www.cr173.com/html/22594_1.html ogre3d环境配置 SDK安装配置及简单事例教程 http://ww ...
- HDU 6112 今夕何夕 蔡勒公式
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6112题意:中文题目 分析:关键点在与如何计算一个日期是星期几,这个可以通过蔡勒公式来计算.基姆拉尔森计 ...
- 解决Mac开机变慢 command +option + P + R
Mac开机变慢怎么办? command +option + P + R 重点是 开机 后 一直按 该4个键不放 听到3声音响 屏幕出现灰暗灰暗几次 开机速度 5s 重置PRAM和NVRAM的方法都是 ...
- Xcode7 iOS9.0 的真机调试
Xcode7的真机调试: 1.Xcode偏好 -> 账号 -> 增加 Apple ID ->显示 free 2.Target 运行 iOS 版本号 3.修正 Team 项 选择 ...
- IE8下面的line-height的bug
当line-height小于正常值时,超出的部分将被剪裁掉
- Median_of_Two_Sorted_Arrays(理论支持和算法总结)
可以将这个题目推广到更naive的情况,找两个排序数组中的第K个最大值(第K个最小值). 1.直接 merge 两个数组,然后求中位数(第K个最大值或者第K个最小值),能过,不过复杂度是 O(n + ...
- ZOJ-3430
Detect the Virus Time Limit: 2 Seconds Memory Limit: 65536 KB One day, Nobita found that his c ...
