R 数据可视化: PCA 主成分分析图

简介

主成分分析（Principal Component Analysis，PCA）是一种无监督的数据降维方法，通过主成分分析可以尽可能保留下具备区分性的低维数据特征。主成分分析图能帮助我们直观地感受样本在降维后空间中的分簇和聚合情况，这在一定程度上亦能体现样本在原始空间中的分布情况，这对于只能感知三维空间的人类来说，不失为一种不错的选择。

再举个形象的栗子，假如你是一本养花工具宣传册的摄影师，你正在拍摄一个水壶。水壶是三维的，但是照片是二维的，为了更全面的把水壶展示给客户，你需要从不同角度拍几张图片。下图是你从四个方向拍的照片：

PCA形象解释说明

第一张图里水壶的背面可以看到，但是看不到前面。

第二张图是拍前面，可以看到壶嘴，这张图可以提供了第一张图缺失的信息，但是壶把看不到了。

第三张俯视图既可以看到壶嘴，也可以看到壶把，但是无法看出壶的高度。

第四张图是你打算放进目录的，水壶的高度，顶部，壶嘴和壶把都清晰可见。

PCA的设计理念与此类似，它可以将高维数据集映射到低维空间的同时，尽可能的保留更多变量。

开始作图

使用 R 语言能做出像 SIMCA-P 一样的 PCA 图吗？

答案是肯定的，使用 R 语言不仅能做出像 SIMCA-P 一样的 PCA 图，还能做出比 SIMCA-P 更好看的图，而且好看的上限仅取决于个人审美风格。

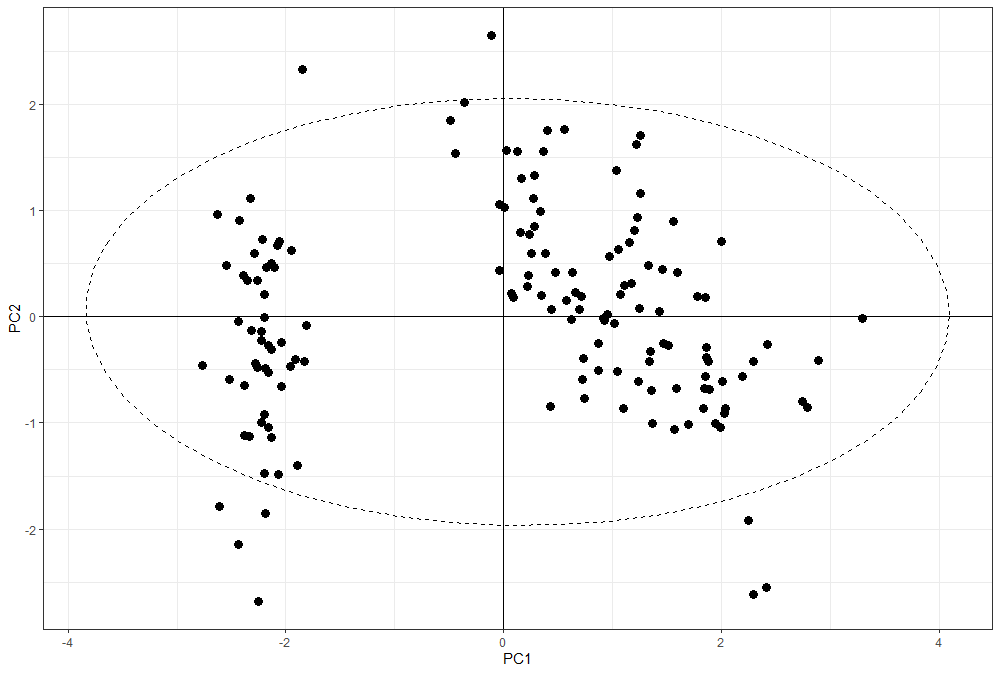
1. PCA 分析图本质上是散点图

主成分分析图 = 散点图 + 置信椭圆，散点的横纵坐标对应 PCA 的第一主成分、第二主成分。

library(ggplot2)

# 数据准备
data = subset(iris, select = -Species)
class = iris[["Species"]]

# PCA
pca = prcomp(data, center = T, scale. = T)
pca.data = data.frame(pca$x)
pca.variance = pca$sdev^2 / sum(pca$sdev^2)

ggplot(pca.data, aes(x = PC1, y = PC2)) +
    geom_point(size = 3) +
    geom_hline(yintercept = 0) +
    geom_vline(xintercept = 0) +
    stat_ellipse(aes(x = PC1, y = PC2), linetype = 2, size = 0.5, level = 0.95) +
    theme_bw()

散点图+椭圆

2. 为不同类别着色

接下来想给散点加上分类颜色：

library(ggplot2)

# 数据准备
data = subset(iris, select = -Species)
class = iris[["Species"]]

# PCA
pca = prcomp(data, center = T, scale. = T)
pca.data = data.frame(pca$x)
pca.variance = pca$sdev^2 / sum(pca$sdev^2)

ggplot(pca.data, aes(x = PC1, y = PC2, color = class)) +
    geom_point(size = 3) +
    geom_hline(yintercept = 0) +
    geom_vline(xintercept = 0) +
    stat_ellipse(aes(x = PC1, y = PC2), linetype = 2, size = 0.5, level = 0.95) +
    theme_bw()

给不同类别样本着色-1

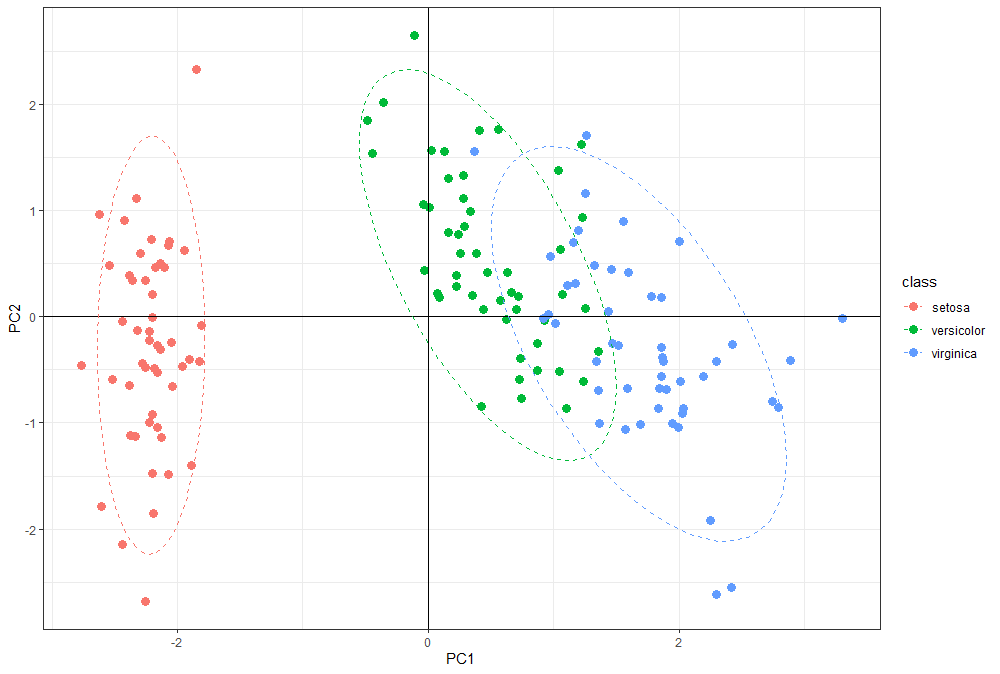
颜色是加上了，但是椭圆咋变成了 3 个？

原来是 stat_ellipse 函数默认对每个类别的数据计算自己的置信区间。如何对多类样本只计算一个置信区间呢？查看 stat_ellipse 的帮助文档：

inherit.aes

default TRUE, If FALSE, overrides the default aesthetics, rather than combining with them. This is most useful for helper functions that define both data and aesthetics and shouldn't inherit behaviour from the default plot specification,

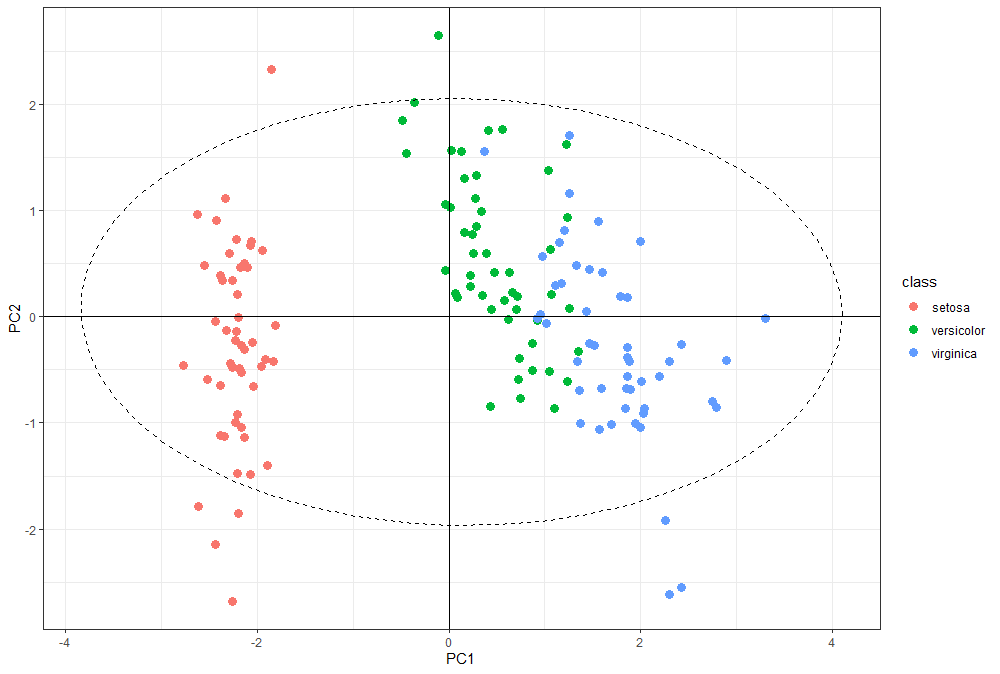
原来是 stat_ellipse 函数默认会继承 ggplot 中的 aes 设置，如果希望 stat_ellipse 使用自己的 aes 设置，需要将参数 inherit.aes 设置为 FALSE。

library(ggplot2)

# 数据准备
data = subset(iris, select = -Species)
class = iris[["Species"]]

# PCA
pca = prcomp(data, center = T, scale. = T)
pca.data = data.frame(pca$x)
pca.variance = pca$sdev^2 / sum(pca$sdev^2)

ggplot(pca.data, aes(x = PC1, y = PC2, color = class)) +
    geom_point(size = 3) +
    geom_hline(yintercept = 0) +
    geom_vline(xintercept = 0) +
    stat_ellipse(aes(x = PC1, y = PC2), linetype = 2, size = 0.5, level = 0.95, inherit.aes = FALSE) +
    theme_bw()

给不同类别样本着色

3. 样式微调

接下来对样式进行微调：为不同类别样本自定义着色，添加 x 轴、y 轴标题，添加 title：

library(ggplot2)

# 数据准备
data = subset(iris, select = -Species)
class = iris[["Species"]]

# PCA
pca = prcomp(data, center = T, scale. = T)
pca.data = data.frame(pca$x)
pca.variance = pca$sdev^2 / sum(pca$sdev^2)

# 自定义颜色
palette = c("mediumseagreen", "darkorange", "royalblue")

ggplot(pca.data, aes(x = PC1, y = PC2, color = class)) +
    geom_point(size = 3) +
    geom_hline(yintercept = 0) +
    geom_vline(xintercept = 0) +
    stat_ellipse(aes(x = PC1, y = PC2), linetype = 2, size = 0.5, level = 0.95, inherit.aes = FALSE) +
    theme_bw() +
    scale_color_manual(values = palette) +
    theme(panel.grid.major.x = element_blank(),
          panel.grid.minor.x = element_blank(),
          panel.grid.major.y = element_blank(),
          panel.grid.minor.y = element_blank()) +
    labs(x = paste0("PC1: ", signif(pca.variance[1] * 100, 3), "%"),
         y = paste0("PC2: ", signif(pca.variance[2] * 100, 3), "%"),
         title = paste0("PCA of iris")) +
    theme(plot.title = element_text(hjust = 0.5))

样式微调

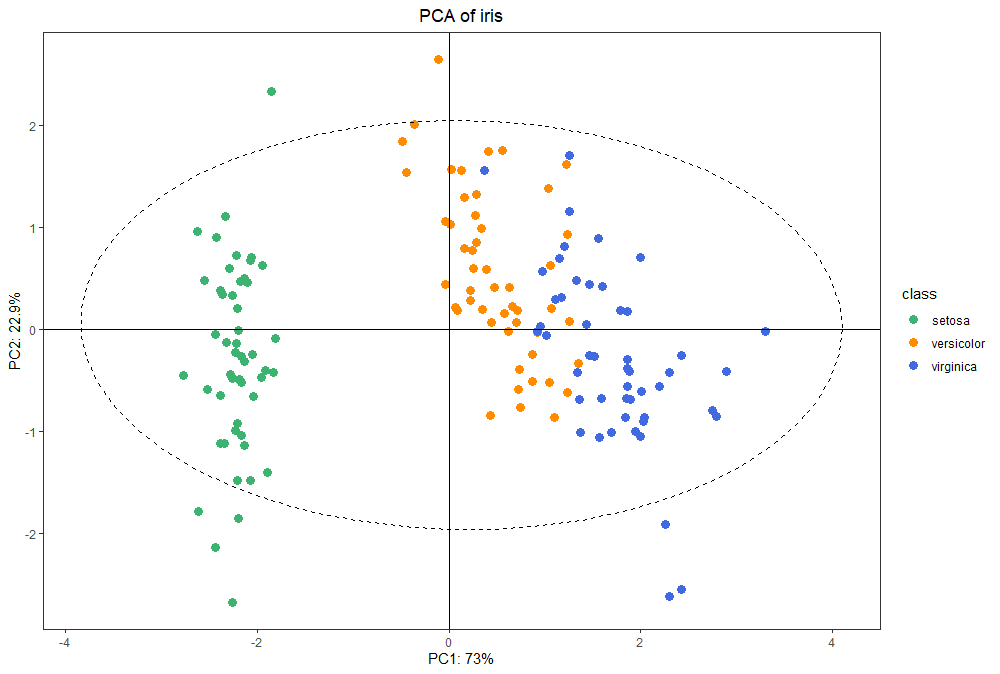
将作图结果和 SIMCA-P 对比，散点、椭圆基本完全一致，只是比它更顺眼一些罢了~

欢迎留言讨论，如果本文有帮助到你，点个赞就更好啦！

参考

[1] Master Machine Learning With scikit-learn

相关文章

[1] R 数据可视化：水平渐变色柱状图

[2] R 数据可视化：双坐标系柱线图

[3] R 数据可视化：BoxPlot

[4] R 数据可视化：环形柱状图