Eolink家族成员回归 — 开源服务Eoapi！

Eolink 开源产品又回来了！Eoapi 自 2016 年上架 Github 以来，一直备受国内外开发者的欢迎和好评 ，在2018年 Eolink 为了进一步升级该产品而进行了暂时下架。时隔四年，Eoapi 现以全新的面孔重新归来！我们致力于为广大开发者提供一款开源、简易、又好用的 API 工具！

▲ Eoapi是什么? ▲

Eoapi 是一款类 Postman 的开源 API 工具，它更轻量，同时可拓展。

支持 API 有关的核心功能，还可以通过插件市场帮助你将 API 发布到各个应用平台，比如发布到网关完成 API 上线，或者和低代码平台结合，将 API 快速变成可使用的组件等。

Eolink 在 2022 年开源了 Eoapi 项目，Eoapi 建立在 APIKit 多年以来在 API 全生命周期领域的行业经验基础之上，同时希望通过开源吸收社区中最棒的想法和实践。

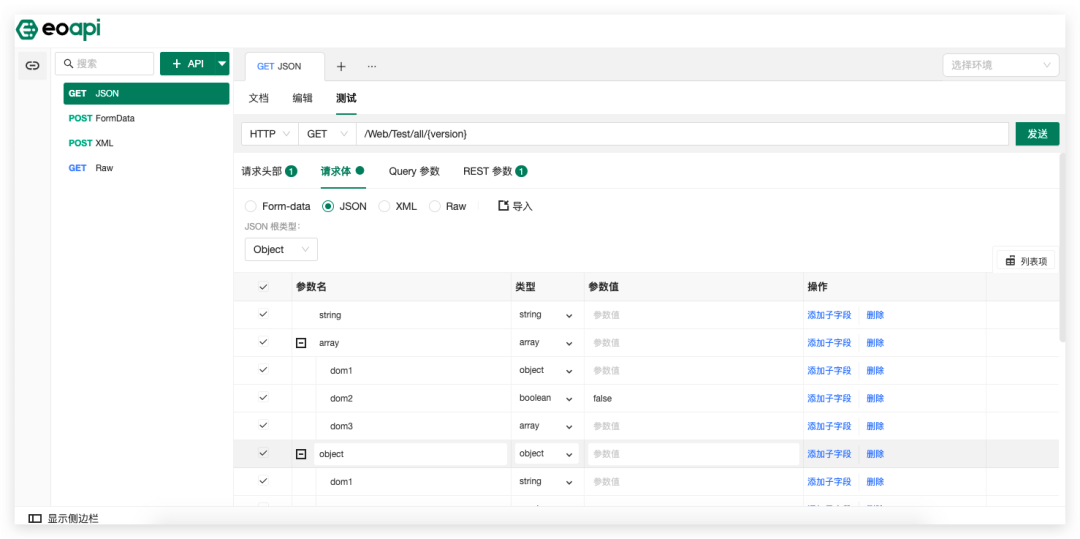
▼ 我们为什么要做 Eoapi ？

在社区中时常会出现“抱怨某商业产品越来越臃肿”的声音，API 工具也是如此。从最早期只做 API 调试的工具，到经过多年的演进后集成全面功能的“庞然大物”，它越来越成熟了，也越来越不适合最初的那批用户了。

我们并不需要用到所有的功能，自然也会觉得自己用不上的功能是“多余”的。

我们希望个性和共性能够共存，因此，我们决定发布这款极其轻量的 API 工具，基础功能仅包括 API 文档和测试，满足开发者最核心的需求。同时：

我们选择支持插件：让每个功能满足所有人的需求是不可能的，通过不断地加功能满足需求只会让产品越做越重。插件系统则不一样，一个插件一个功能，你可以像组装乐高一样组装你想要的功能。

我们选择拥抱开源：我们希望将自己的技术沉淀、解决方案做成开源项目回馈给开源社区，也希望通过开源吸收社区中最棒的想法和实践，联合开发者、企业积极地共创插件生态。

▼ Eoapi 的核心价值是什么？

** 可拓展 **

Eoapi 支持插件系统，插件系统有两点好处：

▲ 可以只选择自己需要的功能，随时插拔

▲ 在遇到不满足现有需求的场景下，可以选择自己动手开发插件

在开源这款产品之前，我们在商业产品中沉淀了大量用户使用 API 管理工具的实践场景，所以官方也会在每年按照一定的频率发布官方插件，将商业产品上的沉淀贡献到开源。

同时我们将会配套相应的文档、插件示例以及提供一系列流畅的开发者体验脚手架，让大家可以快速的上手定制趁手的“兵器”。

▼ 目标用户

▲ 如果你想要快速调试 API，发现现有的 API 工具想要的功能找不到，不想要的功能却重点展示。

▲ 如果你厌烦了在各个平台填写重复的 API 信息，例如帮助你将 API 一键发布到 API 网关，省去手动填写路由的工作。

那么 Eoapi 就是适合你的工具。

▼ 功能介绍

1.API 接口测试

支持 Web 最常见的 HTTP（S） 协议，纯 UI 操作，仅需一次点击即可获取清晰完整的 API 测试信息。

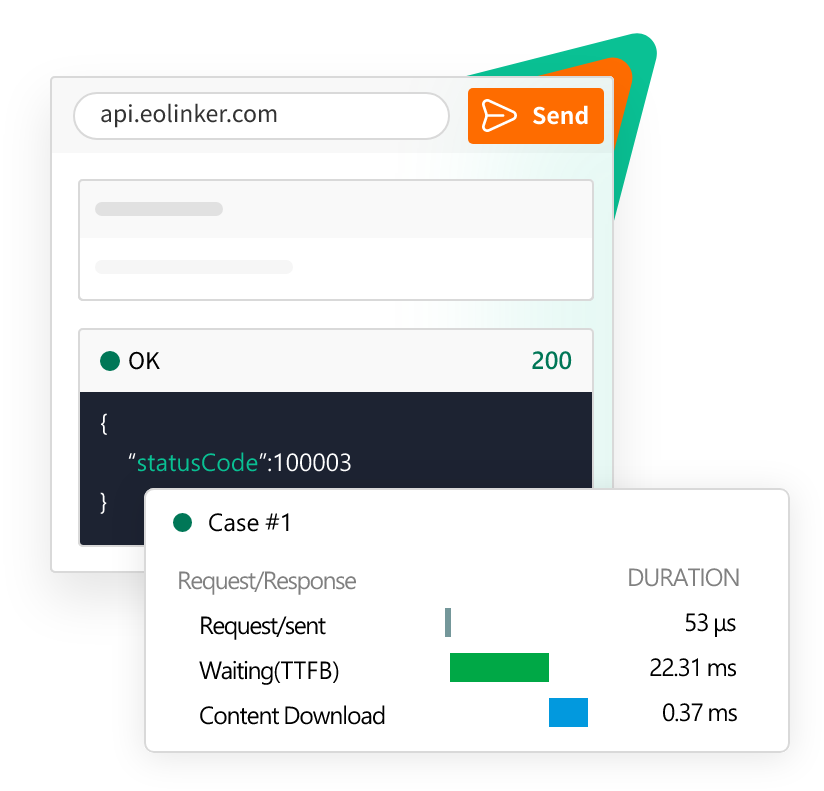
2.API 接口管理

支持规范化的文档、友好的阅读界面以及清晰的分类。

3.插件广场

• 此功能尚未发布，功能预告~ *

需要更多功能？你可以安装语言包、导入 Postman、Swagger 等格式的 API、一键同步到其他平台等插件，总能找到你需要的。

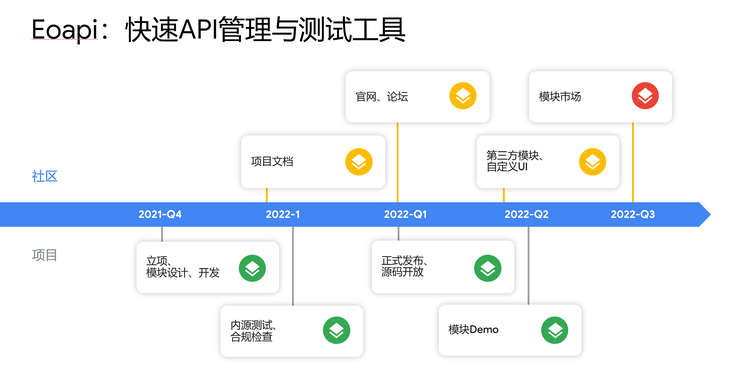
▲ 2022年Roadmap ▲

▲ 结 束 语 ▲

如果你对开源感兴趣，对我们的项目感兴趣，欢迎加入贡献，我们一起共创一个开放且有趣的社区。

可参与的贡献包括不限于：

▲ 提交 issue 反馈需求、Bugs

▲ 贡献官方文档

▲ 推荐大家使用 eoapi 或介绍 eoapi 的功能

▲ 开发一个 eoapi 插件

▲ 参与 eoapi 核心代码开发

期待与你相遇。

图中所使用的的接口管理工具是eoapi，感兴趣可以自行使用！