SETTLE约束算法中的坐标变换问题

技术背景

在之前的两篇文章中，我们分别讲解了SETTLE算法的原理和基本实现和SETTLE约束算法的批量化处理。SETTLE约束算法在水分子体系中经常被用到，该约束算法具有速度快、可并行、精度高的优点。本文我们需要探讨的是该约束算法中的一个细节，问题是这样定义的，给定坐标系\(XYZ\)下的两个已知三角形\(\Delta A_0B_0C_0\)和三角形\(\Delta A_1B_1C_1\)，以三角形\(\Delta A_0B_0C_0\)构造一个平面\(\pi_0\)，将\(\pi_0\)平移到三角形\(\Delta A_1B_1C_1\)的质心位置，作为新坐标系的\(X'Y'\)平面，再使得\(Y'Z'\)平面过\(A_1\)点，以此来构造一个新的坐标系\(X'Y'Z'\)，求两个坐标系之间的变换。

理论推导

坐标系\(OXYZ\)和\(O'X'Y'Z'\)之间的变换，只有平移和旋转，没有伸缩。那么关于平移的部分，我们只需要考虑两个原点位置之间的向量差即可。而旋转部分，需要一些技巧，至少我们需要找到三个合适的点用于计算这个旋转矩阵。比如说，假定三角形\(\Delta A_1B_1C_1\)在坐标系\(OXYZ\)和\(O'X'Y'Z'\)之中的位置都是已知的，那么我们就可以按照下述公式来计算旋转矩阵\(R\)：

\[R\left[
\begin{matrix}
X_A && X_B && X_C\\
Y_A && Y_B && Y_C\\
Z_A && Z_B && Z_C
\end{matrix}
\right]=
\left[
\begin{matrix}
X'_A && X'_B && X'_C\\
Y'_A && Y'_B && Y'_C\\
Z'_A && Z'_B && Z'_C
\end{matrix}
\right]
\]

然后在等式两边各乘上一个逆矩阵就可以得到旋转矩阵：

\[R=\left[
\begin{matrix}
X'_A && X'_B && X'_C\\
Y'_A && Y'_B && Y'_C\\
Z'_A && Z'_B && Z'_C
\end{matrix}
\right]\left[
\begin{matrix}
X_A && X_B && X_C\\
Y_A && Y_B && Y_C\\
Z_A && Z_B && Z_C
\end{matrix}
\right]^{-1}
\]

然而不幸的是，我们并不能直接得到三角形\(\Delta A_1B_1C_1\)在坐标系\(O'X'Y'Z'\)之中的位置，这需要一些计算。因此，我们可以考虑另辟蹊径，找其他更容易计算的三个向量，用来计算我们所需要的旋转矩阵。

第一个向量

我们找的第一个向量是\(Z'\)轴，或者用向量表示就是\(\vec{O'Z'}=[0, 0, 1]^T\)，因为\(Z'\)轴跟平面\(\pi_0\)是垂直的关系，也就是垂直于三角形\(\Delta A_0B_0C_0\)。因此对应的可以用三角形\(\Delta A_0B_0C_0\)的任意两条边的外积来计算向量\(\vec{O'Z'}=R\cdot[\vec{A_0B_0}\times \vec{A_0C_0}]\)（注意做归一化处理）。

第二个向量

如果分别用\(D_1\)和\(D'_1\)来表示三角形\(\Delta A_1B_1C_1\)在坐标系\(OXYZ\)和坐标系\(O'X'Y'Z'\)下的质心位置。这里我们找的第二个向量，就是\(\vec{D'_1A'_1}\)。这里因为\(A'_1\)点在\(Y'Z'\)平面上，因此\(X'_{A'_1}=0\)。而向量\(\vec{D'_1A'_1}\)和\(Z'\)轴的夹角，我们可以在坐标系\(OXYZ\)下计算：

\[cos \theta=\frac{(\vec{A_0B_0}\times \vec{A_0C_0})\cdot\vec{D_1A_1}}{|\vec{A_0B_0}\times \vec{A_0C_0}|\cdot|\vec{D_1A_1}|}, sin \theta=\sqrt{1-cos^2\theta}
\]

计算出来夹角之后，就可以得到\(\vec{D'_1A'_1}=[0, sin\theta, cos\theta]^T\)，即：\(\vec{D'_1A'_1}=R\cdot\vec{D_1A_1}\)。

第三个向量

到这一步为止，其实我们还是没有计算出\(\vec{D'_1B'_1}\)和\(\vec{D'_1C'_1}\)的值，因此我们第三个向量，在前两个向量的基础之上，用叉乘的方法再构造一个\(X'\)轴的向量，即\(\vec{O'X'}=[1, 0, 0]^T\)，旋转矩阵计算方法为：

\[\vec{O'X'}=R\cdot \left[(\vec{A_0B_0}\times \vec{A_0C_0})\times \vec{D_1A_1}\right]
\]

小结

这样一来，我们就得到了三个向量在两个坐标系下的坐标，可以用于建立方程组，计算两个坐标之间的变换关系，如果写成矩阵乘法形式就是：

\[R = \left[
\begin{matrix}
0&&0&&1\\
0&&\sqrt{1-(\frac{(\vec{A_0B_0}\times \vec{A_0C_0})\cdot\vec{D_1A_1}}{|\vec{A_0B_0}\times \vec{A_0C_0}|\cdot|\vec{D_1A_1}|})^2}&&0\\
1&&\frac{(\vec{A_0B_0}\times \vec{A_0C_0})\cdot\vec{D_1A_1}}{|\vec{A_0B_0}\times \vec{A_0C_0}|\cdot|\vec{D_1A_1}|}&&0
\end{matrix}
\right]\left(\left[
\begin{matrix}
\vec{A_0B_0}\times \vec{A_0C_0}\\
\vec{D_1A_1}\\
(\vec{A_0B_0}\times \vec{A_0C_0})\times \vec{D_1A_1}
\end{matrix}
\right]^{T}\right)^{-1}
\]

代码实现

这里先提一下代码实现和测试的思路。我们首先用Python来构造2个三角形，得到一个新的三角形。然后我们再根据上述的公式，计算得到一个坐标旋转矩阵。最后我们再输入一些便于手动计算的点（或者是直接用前面三角形的三个角，或者是中间的一些向量都是可以的），用旋转矩阵进行变换，来测试一下是否我们所需要的坐标变换之后的结果。

In [1]: import numpy as np

In [2]: T0 = np.array([[0, 0, 1], [0, -1, 0],[0, 1, 0]], np.float32)

In [3]: T1 = np.array([[1, 0, 1], [0, -1, 0], [0, 1, 0]], np.float32)

In [4]: D0 = np.mean(T0, axis=-2)

In [5]: D1 = np.mean(T1, axis=-2)

In [6]: A0B0 = T0[1]-T0[0]

In [7]: A0C0 = T0[2]-T0[0]

In [8]: v0 = np.cross(A0B0, A0C0)

In [9]: v0 /= np.linalg.norm(v0)

In [10]: v1 = T1[0]-D1

In [11]: v1 /= np.linalg.norm(v1)

In [12]: v2 = np.cross(v0, v1)

In [13]: v2 /= np.linalg.norm(v2)

In [14]: M1 = np.vstack((v0, v1, v2))

In [15]: M1 = M1.T

In [16]: iM1 = np.linalg.inv(M1)

In [17]: cost = np.dot(v0, v1)/np.linalg.norm(v0)/np.linalg.norm(v1)

In [18]: M0 = np.array([[0, 0, 1], [0, np.sqrt(1 - cost**2), 0], [1, cost, 0]])

In [19]: R = np.dot(M0, iM1)

In [20]: R
Out[20]:
array([[ 0.00000000e+00, -1.00000000e+00,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  9.99999916e-01],
       [ 1.00000000e+00,  0.00000000e+00,  5.00651538e-08]])

In [21]: np.dot(R, v0)
Out[21]: array([0., 0., 1.])

In [22]: np.dot(R, v1)
Out[22]: array([0.        , 0.70710671, 0.7071068 ])

In [23]: np.dot(R, v2)
Out[23]: array([1., 0., 0.])

In [24]: np.dot(R, T1[0]-D1)
Out[24]: array([0.        , 0.66666657, 0.66666666])

In [25]: np.dot(R, T1[1]-D1)
Out[25]: array([ 1.        , -0.33333332, -0.33333336])

In [26]: np.dot(R, T1[2]-D1)
Out[26]: array([-1.        , -0.33333332, -0.33333336])

上面这个案例的流程是这样的，我们先创建两个不一样大小的绿色三角形和红色三角形，我们将要做的事情是以绿色三角形为\(X'Y'\)平面，红色三角形的质心为原点，并使得\(Y'Z'\)平面过\(A_1\)点，以此来构造一个新的坐标系，并计算前后两个坐标系之间的变换。

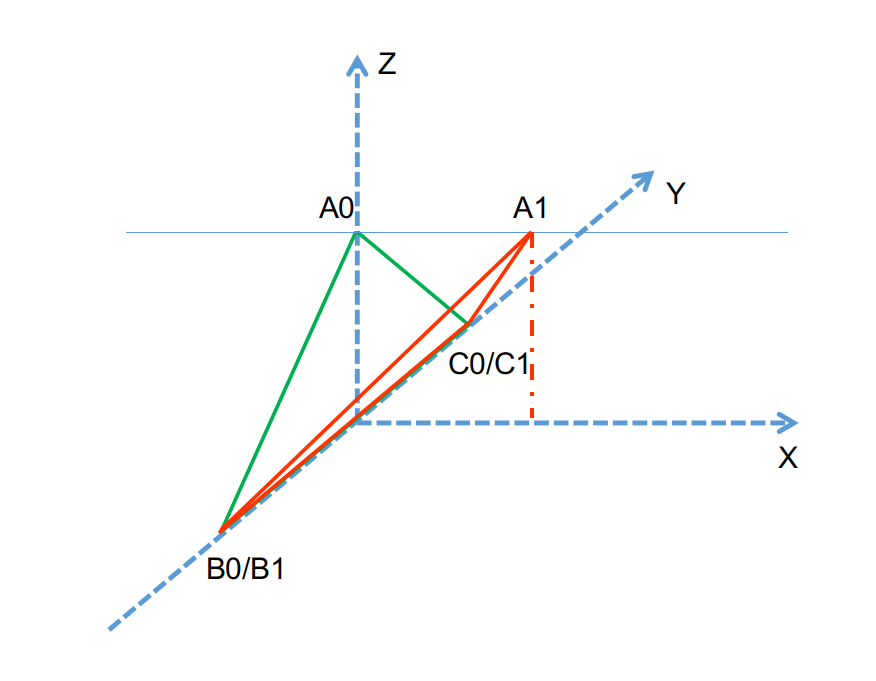
这里需要一些空间想象能力，我们可以先将绿色的三角形平面平移到过红色三角形的质心位置，同时将坐标系原点移动到红色三角形的质心位置，再旋转坐标轴，使得\(Y'Z'\)平面过\(A_1\)点。这样一来通过上一个章节中的旋转矩阵的构造方法，我们就可以计算出所有的向量在两个坐标系下的旋转变换。

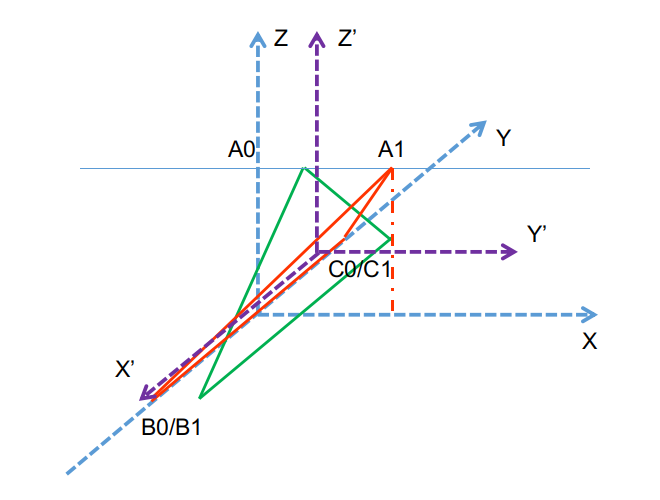
当然，需要注意的是，这个变换只是一个旋转变换，由于坐标系发生了平移，所以需要有一个固定的参考点，才能够精确的得到某一个给定的点的坐标变换。比如我们上述python代码中的24、25、26都是对红色三角形的三个顶点关于质心的相对位置的坐标变换，在坐标变换前后，顶点坐标都需要减去质心的坐标。

总结概要

在已知两个三角形顶点坐标的情况下，我们要以其中的一个三角形平面去构造一个新的坐标系，并且需要找到新旧坐标系之间的变换关系。这是一个比较简单的立体几何的问题，寻找两个坐标系之间的变换矩阵。如果是常规思路，可以先根据两个三角形之间的相对位置去计算一下在新坐标系下两个三角形的新的顶点坐标，从而可以取三个点来构造一个坐标变换矩阵，进而推广到所有向量在这两个坐标系之间的变换关系。而本文提供了一种相对更容易求解、也比较直接的思路，并给出了相关的Python代码实现过程。

版权声明

本文首发链接为：https://www.cnblogs.com/dechinphy/p/xyz-transform.html

作者ID：DechinPhy

更多原著文章请参考：https://www.cnblogs.com/dechinphy/

打赏专用链接：https://www.cnblogs.com/dechinphy/gallery/image/379634.html

腾讯云专栏同步：https://cloud.tencent.com/developer/column/91958

CSDN同步链接：https://blog.csdn.net/baidu_37157624?spm=1008.2028.3001.5343

51CTO同步链接：https://blog.51cto.com/u_15561675