最短路径算法-迪杰斯特拉(Dijkstra)算法在c#中的实现和生产应用

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。

它的主要特点是以起始点为中心向外层层扩展(广度优先遍历思想)，直到扩展到终点为止

贪心算法(Greedy Algorithm)

贪心算法，又名贪婪法，是寻找最优解问题的常用方法，这种方法模式一般将求解过程分成若干个步骤，但每个步骤都应用贪心原则，选取当前状态下最好/最优的选择（局部最有利的选择），并以此希望最后堆叠出的结果也是最好/最优的解。

Dijkstra推导过程(摘自：https://zhuanlan.zhihu.com/p/346558578)

• 通过Dijkstra计算图G中的最短路径时，需要指定一个起点D(即从顶点D开始计算)。
• 此外，引进两个数组S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点D的距离)。
• 初始时，数组S中只有起点D；数组U中是除起点D之外的顶点，并且数组U中记录各顶点到起点D的距离。如果顶点与起点D不相邻，距离为无穷大。
• 然后，从数组U中找出路径最短的顶点K，并将其加入到数组S中；同时，从数组U中移除顶点K。接着，更新数组U中的各顶点到起点D的距离。
• 重复第4步操作，直到遍历完所有顶点。

图解(摘自：https://zhuanlan.zhihu.com/p/346558578)

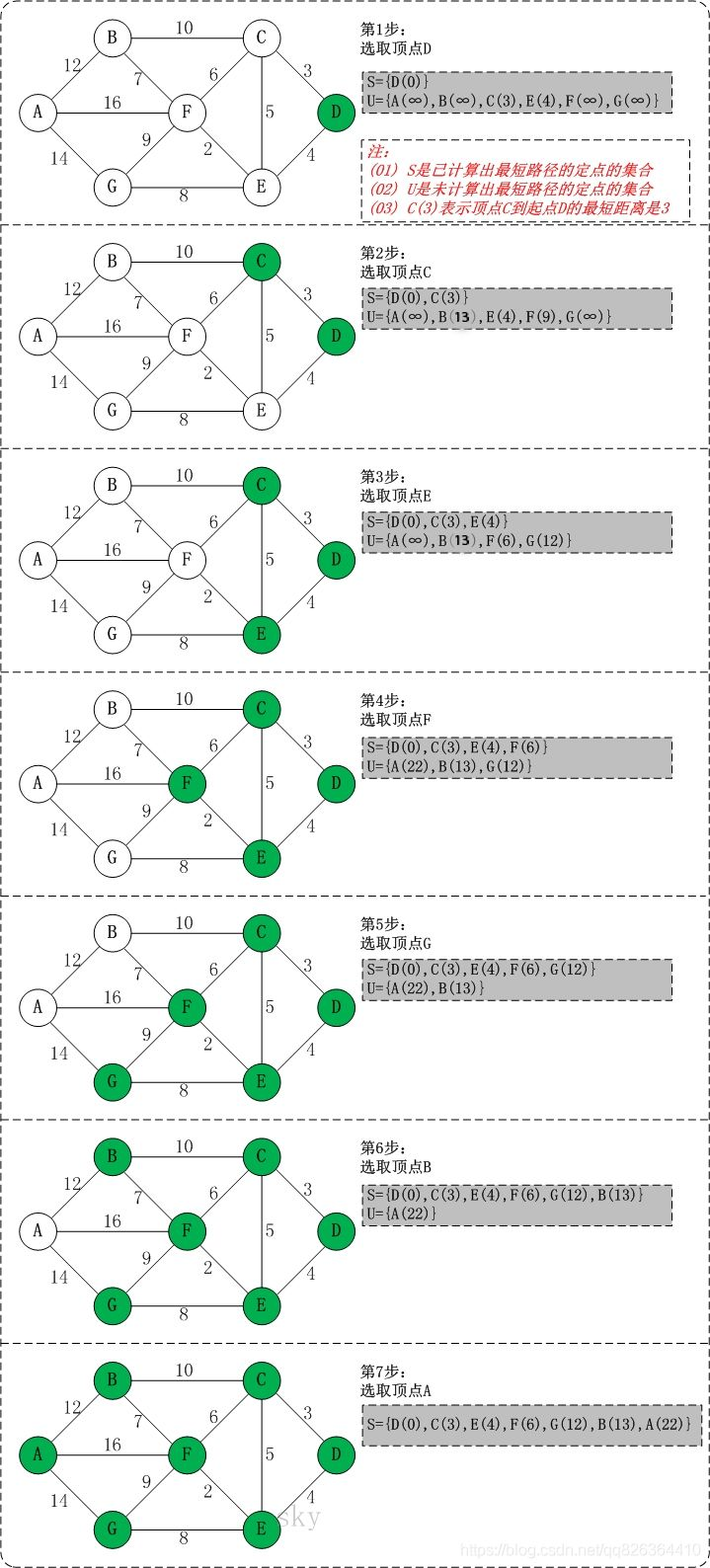
当我们理解了算法原理后，我们需要明白Dijkstra不能够处理的场景

• 不能处理负权重边(往往找错最短路径,在Dijkstra看来,cost是递增的)
• A-A的绕圈路径查找(需要特殊处理)

代码实战(已经在生产使用)

• 节点对象定义：

public class Edge
    {
        public int StartNodeID;
        public int EndNodeID;
        public double Weight;
    }
public class Node
    {
        public int Id { get; set; }
        public bool Enable { get; set; }
    }
public class NodeItem
        {
            public bool Used { get; set; }
            public List<int> Nodes { get; } = new List<int>();
            public int NodeId { get; set; }
            public int Index { get; set; }
            public double Weight { get; set; }
        }

• 初始化图，点，路径集合

public void Initialize(IEnumerable<Edge> edges, IEnumerable<Node> nodes)
        {
            _edges = edges.ToList();
            _nodes = nodes.ToList();
            _nodeItems = new List<NodeItem>();
            _graph = new double[_nodes.Count(), _nodes.Count()];
            foreach (var row in Enumerable.Range(0, _nodes.Count()))
            {
                var rowNode = _nodes[row];
                foreach (var colnum in Enumerable.Range(0, _nodes.Count()))
                {
                    if (row == colnum)
                    {
                        _graph[row, colnum] = 0;
                        continue;
                    }
                    var edge = _edges.FirstOrDefault(x =>
                            x.StartNodeID == rowNode.Id && x.EndNodeID == _nodes[colnum].Id);
                    _graph[row, colnum] = edge == null ? double.MaxValue : edge.Weight;
                }

                _nodeItems.Add(new NodeItem()
                {
                    NodeId = _nodes[row].Id,
                    Index = row,
                    Weight = double.MaxValue
                });
            }
        }

• 路由主体方法

public Route GetRoute(int startPointID, int endPointID)
        {
            if (IsRouting)
                throw new InvalidOperationException($"can't route.router busy");

            IsRouting = true;
            Node sNode = null;
            Node dNode = null;

            try
            {
                if ((sNode = _nodes.FirstOrDefault(x => x.Id == startPointID)) == null
                    || (dNode = _nodes.FirstOrDefault(x => x.Id == endPointID)) == null)
                    throw new ArgumentNullException("can't found target points.");

                _nodeItems.FirstOrDefault(x => x.NodeId == startPointID).Used = true;
                _nodeItems.ForEach(x =>
                {
                    x.Weight = GetRowArray(_graph, _nodes.IndexOf(sNode))[x.Index];
                    x.Nodes.Add(startPointID);
                });

                while (_nodeItems.Any(x => !x.Used))
                {
                    var item = GetUnUsedAndMinNodeItem();
                    if (item == null)
                        break;

                    item.Used = true;
                    var tempRow = GetRowArray(_graph, item.Index);
                    foreach (var nodeItem in _nodeItems)
                    {
                        if (nodeItem.Weight > tempRow[nodeItem.Index] + item.Weight)
                        {
                            nodeItem.Weight = tempRow[nodeItem.Index] + item.Weight;
                            nodeItem.Nodes.Clear();
                            nodeItem.Nodes.AddRange(item.Nodes);
                            nodeItem.Nodes.Add(item.NodeId);
                        }
                    }
                }

                var desNodeitem = _nodeItems.FirstOrDefault(x => x.NodeId == endPointID);
                if (desNodeitem.Used && desNodeitem.Weight < double.MaxValue)
                {
                    var edges = new List<Edge>();
                    foreach (var index in Enumerable.Range(0, desNodeitem.Nodes.Count - 1))
                    {
                        edges.Add(_edges.FirstOrDefault(x => x.StartNodeID == desNodeitem.Nodes[index] && x.EndNodeID == desNodeitem.Nodes[index + 1]));
                    }

                    edges.Add(_edges.FirstOrDefault(x => x.StartNodeID == desNodeitem.Nodes.Last() && x.EndNodeID == endPointID));
                    return new Route()
                    {
                        Edges = edges
                    };
                }

                return null;
            }
            catch (Exception ex)
            {
                _logger.LogError(ex.ToString());
                _logger.LogInformation($"startPoint:{startPointID}-endpoint:{endPointID} route faild.");
                throw;
            }
            finally
            {
                _nodeItems.ForEach(x =>
                {
                    x.Used = false;
                    x.Nodes.Clear();
                });

                IsRouting = false;
            }
        }

        private NodeItem GetUnUsedAndMinNodeItem()
        {
            return _nodeItems.Where(x => !x.Used && x.Weight != double.MaxValue).OrderBy(x => x.Weight).FirstOrDefault();
        }

        private double[] GetRowArray(double[,] source, int row)
        {
            double[] result = new double[source.GetLength(1)];
            foreach (var index in Enumerable.Range(0, result.Length))
            {
                result[index] = source[row, index];
            }

            return result;
        }

完整代码

public class DijkstraRouter
    {
        private double[,] _graph;
        private List<Edge> _edges;//所有的边
        private List<Node> _nodes;//所有的节点
        private List<NodeItem> _nodeItems;
        public bool IsRouting { get; set; }

        private readonly ILogger<DijkstraRouter> _logger;

        public DijkstraRouter(ILogger<DijkstraRouter> logger)
        {
            _logger = logger;
        }

        public Route GetRoute(int startPointID, int endPointID)
        {
            if (IsRouting)
                throw new InvalidOperationException($"can't route.router busy");

            IsRouting = true;
            Node sNode = null;
            Node dNode = null;

            try
            {
                if ((sNode = _nodes.FirstOrDefault(x => x.Id == startPointID)) == null
                    || (dNode = _nodes.FirstOrDefault(x => x.Id == endPointID)) == null)
                    throw new ArgumentNullException("can't found target points.");

                _nodeItems.FirstOrDefault(x => x.NodeId == startPointID).Used = true;
                _nodeItems.ForEach(x =>
                {
                    x.Weight = GetRowArray(_graph, _nodes.IndexOf(sNode))[x.Index];
                    x.Nodes.Add(startPointID);
                });

                while (_nodeItems.Any(x => !x.Used))
                {
                    var item = GetUnUsedAndMinNodeItem();
                    if (item == null)
                        break;

                    item.Used = true;
                    var tempRow = GetRowArray(_graph, item.Index);
                    foreach (var nodeItem in _nodeItems)
                    {
                        if (nodeItem.Weight > tempRow[nodeItem.Index] + item.Weight)
                        {
                            nodeItem.Weight = tempRow[nodeItem.Index] + item.Weight;
                            nodeItem.Nodes.Clear();
                            nodeItem.Nodes.AddRange(item.Nodes);
                            nodeItem.Nodes.Add(item.NodeId);
                        }
                    }
                }

                var desNodeitem = _nodeItems.FirstOrDefault(x => x.NodeId == endPointID);
                if (desNodeitem.Used && desNodeitem.Weight < double.MaxValue)
                {
                    var edges = new List<Edge>();
                    foreach (var index in Enumerable.Range(0, desNodeitem.Nodes.Count - 1))
                    {
                        edges.Add(_edges.FirstOrDefault(x => x.StartNodeID == desNodeitem.Nodes[index] && x.EndNodeID == desNodeitem.Nodes[index + 1]));
                    }

                    edges.Add(_edges.FirstOrDefault(x => x.StartNodeID == desNodeitem.Nodes.Last() && x.EndNodeID == endPointID));
                    return new Route()
                    {
                        Edges = edges
                    };
                }

                return null;
            }
            catch (Exception ex)
            {
                _logger.LogError(ex.ToString());
                _logger.LogInformation($"startPoint:{startPointID}-endpoint:{endPointID} route faild.");
                throw;
            }
            finally
            {
                _nodeItems.ForEach(x =>
                {
                    x.Used = false;
                    x.Nodes.Clear();
                });

                IsRouting = false;
            }
        }

        private NodeItem GetUnUsedAndMinNodeItem()
        {
            return _nodeItems.Where(x => !x.Used && x.Weight != double.MaxValue).OrderBy(x => x.Weight).FirstOrDefault();
        }

        private double[] GetRowArray(double[,] source, int row)
        {
            double[] result = new double[source.GetLength(1)];
            foreach (var index in Enumerable.Range(0, result.Length))
            {
                result[index] = source[row, index];
            }

            return result;
        }

        public void Initialize(IEnumerable<Edge> edges, IEnumerable<Node> nodes)
        {
            _edges = edges.ToList();
            _nodes = nodes.ToList();
            _nodeItems = new List<NodeItem>();
            _graph = new double[_nodes.Count(), _nodes.Count()];
            foreach (var row in Enumerable.Range(0, _nodes.Count()))
            {
                var rowNode = _nodes[row];
                foreach (var colnum in Enumerable.Range(0, _nodes.Count()))
                {
                    if (row == colnum)
                    {
                        _graph[row, colnum] = 0;
                        continue;
                    }
                    var edge = _edges.FirstOrDefault(x =>
                            x.StartNodeID == rowNode.Id && x.EndNodeID == _nodes[colnum].Id);
                    _graph[row, colnum] = edge == null ? double.MaxValue : edge.Weight;
                }

                _nodeItems.Add(new NodeItem()
                {
                    NodeId = _nodes[row].Id,
                    Index = row,
                    Weight = double.MaxValue
                });
            }
        }

        public class NodeItem
        {
            public bool Used { get; set; }
            public List<int> Nodes { get; } = new List<int>();
            public int NodeId { get; set; }
            public int Index { get; set; }
            public double Weight { get; set; }
        }
    }