B树-删除

B树系列文章

1. B树-介绍

2. B树-查找

3. B树-插入

4. B树-删除

删除

根据B树的以下两个特性

• 每一个非叶子结点（除根结点）最少有 ⌈m/2⌉ 个子结点
• 有k个子结点的非叶子结点拥有 k − 1 个键

因此，每个结点存放键的数量的下限的是m/2，

删除操作后减少结点的数量，可能导致导致结点“不饱和”

删除操作的重点和难点在于结点“不饱和”后的再平衡操作

先看下，结点“不饱和”后的再平衡处理

• 如果缺少键结点的右兄弟存在且拥有多余的键，那么向左旋转

假设有一棵3阶B树，如下图所示

3阶B树每个结点的键的数量下限为1

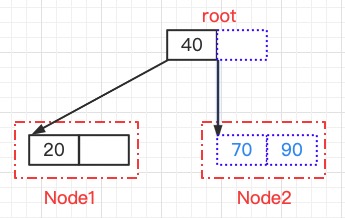
这里删除20这个键，如下图所示

使得Node1结点键的数量为0，导致Node3"不饱和"

通过观察，Node1的右兄弟结点Node2有多余的结点，

即Node2结点的键数量大于1，即使减少一个也不会导致“不饱和”

Node1和Node2的分隔值40，这个分隔值大于Node1的所有键值(如果有到话) ，小于Node2的所有键值

因此，可以将父结点的键值下放到Node1，Node2结点的最小键值提升到父结点，使得Node1脱离“不饱和”状态，使得该B树恢复平衡状态

 

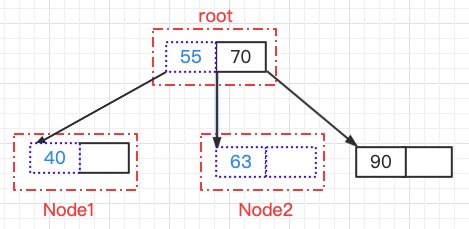
这个平衡操作，键值从右往左移动，因此也叫做左旋操作

 

• 否则，如果缺少键结点的左兄弟存在且拥有多余的键，那么向右旋转

假设有一棵3阶B树，如下图所示

3阶B树每个结点的键的数量下限为1

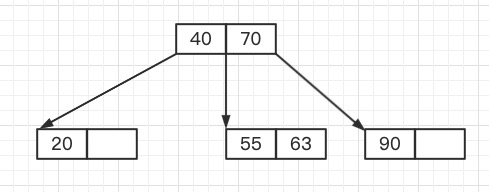
这里删除90这个键，使得Node3结点键的数量为0，导致Node3"不饱和"

通过观察，Node3的左兄弟结点Node2有多余的结点，

即Node2结点的键数量大于1，即使减少一个也不会导致“不饱和”

Node3和Node2的分隔值70，这个分隔值大于Node2的所有键值，小于Node3的所有键值(如果有到话)

父结点的键值下放到Node3，Node2结点的最大键值提升到父结点，，使得Node3脱离“不饱和”状态，使得该B树恢复平衡状态

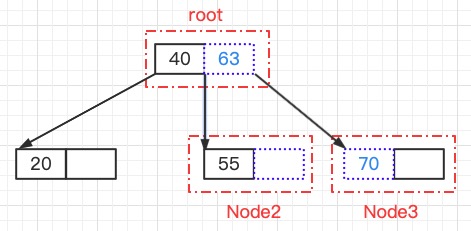
这个平衡操作，键值从左往右移动，因此也叫做右旋操作

• 否则，如果它的两个直接兄弟结点都只有最小数量的键，那么将它与一个直接兄弟结点以及父结点中它们的分隔值合并

假设有一棵3阶B树，如下图所示

3阶B树每个结点的键的数量下限为1

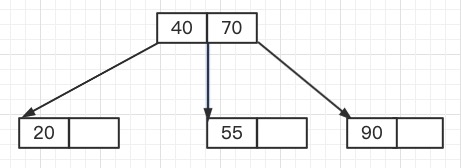
这里删除55这个键，如下图所示

使得Node2结点键的数量为0，导致Node2"不饱和"

通过观察，Node2的左兄弟结点Node1和右兄弟结点Node3都没有多余的键

因此，可以让Node2与左右兄弟结点的任意一个结点进行合并，这里采用和右兄弟结点合并

将Node3结点合并到Node2的操作如下：

将Node2与Node3的在父结点中的分隔值，即70挪到Node2的末尾，

Node3结点的键值挪到Node2的末尾

最终结果如下图所示

问题：合并Node2和Node3是否会导致Node2“溢出”？

1. 首先Node2减少一个键，恰好小于键数量的下限，即此时Node2的键个数为m/2-1

2. Node2增加一个Node2与Node3的分隔值，此时数量为m/2

3. Node3“不饱和”，即Node3的数量小于m/2

4. 因此合并之后，Node2的键数量小于m，而Node2的键数量上限为m-1

5. 所以不会“溢出”

前面的举例，B树是一个3阶B树，删除的都是叶子结点。

当要删除结点位于中间结点时，

可以选择一个新的分隔符（左子树中最大的键或右子树中最小的键），将它从叶子结点中移除，替换掉被删除的键作为新的分隔值。

这里可能导致叶子结点“不饱和”，因此可能需要从叶子结点开始进行再平衡操作

当中间结点“不饱和”时，旋转或者合并操作，在移动键值的时候，相应的儿子结点也需要同步移动

总结下来

删除操作的步骤如下

• 搜索要删除的键值
• 如果该键值在叶子结点，将它从中删除
• 如果该叶子结点“不饱和”，按照后面 “删除后重新平衡”部分的描述重新调整树

如果该键值在非叶子结点，我们注意到左子树中最大的键值仍然小于分隔值。同样的，右子树中最小的键值仍然大于分隔值

• 选择一个新的分隔符（左子树中最大的键或右子树中最小的键值），将它从叶子结点中移除，替换掉被删除的键值作为新的分隔值。
• 前一步删除了一个叶子结点中的键值。如果这个叶子结点拥有的键值数量小于最低要求，那么从这一叶子结点开始重新进行平衡。

删除后重新平衡

• 如果缺少键结点的右兄弟存在且拥有多余的键，那么向左旋转
  1. 将父结点的分隔值复制到缺少键的键值列表的最后（分隔值被移下来；缺少键的结点现在有最小数量的键）
  2. 将右兄弟的第一个儿子结点复制到缺少键的儿子列表的最后
  3. 右兄弟的第一个键覆盖父结点中的分隔值（右兄弟失去了一个结点但仍然拥有最小数量的键）
  4. 右兄弟的键、儿子结点整体往前移动一个单位，即删除第一键和儿子
  5. 树又重新平衡
• 否则，如果缺少键结点的左兄弟存在且拥有多余的键，那么向右旋转
  1. 缺少键结点的键、儿子结点整体往后移动一个单位
  2. 将父结点的分隔值复制到缺少键结点的键列表的第一个位置（分隔值被移下来；缺少键的结点现在有最小数量的键）
  3. 同时需要将左兄弟的最后一个儿子复制到缺少键结点的儿子列表的第一个位置
  4. 左兄弟的最后一个键覆盖父结点中的分隔值（左兄弟失去了一个结点但仍然拥有最小数量的键）
  5. 树又重新平衡
• 否则，如果它的两个直接兄弟结点都只有最小数量的键，那么将它与一个直接兄弟结点以及父结点中它们的分隔值合并
  1. 将分隔值复制到左边的结点的键值列表的最后（左边的结点可以是缺少键的结点或者拥有最小数量键的兄弟结点）
  2. 将右边结点中所有的键值移动到左边结点的键值列表（左边结点现在拥有最大数量的键，右边结点为空）
  3. 将右边结点中所有儿子结点移动到左边结点的儿子结点列表
  4. 将父结点中的分隔值和空的右子树移除（父结点失去了一个键）
     • 如果父结点是根结点并且没有键了，那么释放它并且让合并之后的结点成为新的根结点（树的深度减小）
     • 否则，如果父结点的键数量小于最小值，重新平衡父结点

这里是删除的代码

/**
* 删除结点内的某个key
**/
func (bTreeNode *BTreeNode) removeKey(idx int) {
    if bTreeNode.isLeaf { // 叶子结点
        copy(bTreeNode.keyList[idx:], bTreeNode.keyList[idx+1:])
        bTreeNode.keyNum -= 1
    } else {
        // 在叶子结点找一个元素替换掉被删除结点
        leftChild := bTreeNode.leafList[idx]
        rightChild := bTreeNode.leafList[idx+1]
        var tmp *BTreeNode
        if leftChild != nil {
            // 从左儿子结点中找到最大的,替换掉被删除的key
            tmp = leftChild
            for !tmp.isLeaf {
                tmp = tmp.leafList[bTreeNode.keyNum]
            }
            bTreeNode.keyList[idx] = tmp.keyList[tmp.keyNum-1]
            tmp.keyNum -= 1
        } else if rightChild != nil {
            // 从右儿子结点找到最小的,替换掉被删除的key
            tmp = rightChild
            for !tmp.isLeaf {
                tmp = tmp.leafList[0]
            }
            bTreeNode.keyList[idx] = tmp.keyList[0]
            tmp.keyNum -= 1
        } else {
            fmt.Println("wrong!!!!")
        }
    }
}

/**
* 左旋
**/
func (bTreeNode *BTreeNode) leftShift(idx int) {
    pos := idx
    if idx == 0 {
        pos = 1
    }
    curNode := bTreeNode.leafList[idx]
    rightBro := bTreeNode.leafList[pos]
    // 将父节点的分隔值复制到缺少元素节点的最后,（分隔值被移下来；缺少元素的节点现在有最小数量的元素）
    curNode.keyList[bTreeNode.keyNum] = bTreeNode.keyList[idx]
    curNode.keyNum += 1
    // 兄弟结点的左儿子 作为 缺少元素节点 的右儿子
    curNode.leafList[bTreeNode.keyNum] = rightBro.leafList[0]

    // 将父节点的分隔值替换为右兄弟的第一个元素
    curNode.keyList[idx] = rightBro.keyList[0]

    // 右兄弟结点少了个元素
    copy(rightBro.keyList, rightBro.keyList[1:])
    copy(rightBro.leafList, rightBro.leafList[1:])
    rightBro.keyNum -= 1
}

/**
* 右旋
**/
func (bTreeNode *BTreeNode) rightShift(idx int) {
    pos := idx
    if pos == 0 {
        pos = 1
    }
    curNode := bTreeNode.leafList[idx]
    leftBro := bTreeNode.leafList[pos-1]
    // 当前结点数据往后一个位置
    copy(bTreeNode.leafList[1:], bTreeNode.leafList)
    copy(bTreeNode.keyList[1:], bTreeNode.keyList)
    // 将父节点的分隔值复制到缺少元素节点的第一个节点
    curNode.keyList[0] = bTreeNode.keyList[idx]
    curNode.keyNum += 1
    curNode.leafList[0] = leftBro.leafList[leftBro.keyNum] // 左兄弟的最后一个儿子放到当前结点的第一个儿子的位置

    curNode.keyList[idx] = leftBro.keyList[leftBro.keyNum-1] // 将父节点的分隔值替换为左兄弟的最后一个元素
    leftBro.keyNum -= 1
}

/**
* 合并
* 将分隔值及左右儿子结点合并
**/
func (bTreeNode *BTreeNode) merge(curNode *BTreeNode, idx int) {
    pos := idx
    if pos == 0 {
        pos = 1
    }
    leftBro := bTreeNode.leafList[pos-1]
    rightBro := bTreeNode.leafList[pos]
    // 将分隔值复制到左边的节点（左边的节点可以是缺少元素的节点或者拥有最小数量元素的兄弟节点）
    leftBro.keyList[leftBro.keyNum] = bTreeNode.keyList[pos-1]
    leftBro.keyNum += 1
    // 将分隔值的右边节点中所有的元素移动到左边节点（左边节点现在拥有最大数量的元素，右边节点为空）
    if rightBro != nil {
        copy(leftBro.leafList[curNode.keyNum:], rightBro.leafList)
        copy(leftBro.keyList[curNode.keyNum:], rightBro.keyList)
        leftBro.keyNum += rightBro.keyNum
    }

    // 将父节点中的分隔值和空的右子树移除（父节点失去了一个元素）
    copy(bTreeNode.keyList[pos-1:], bTreeNode.keyList[pos:])
    copy(bTreeNode.leafList[pos:], bTreeNode.leafList[pos+1:])
    bTreeNode.keyNum -= 1
}

/**
* 删除
**/
func (bTreeNode *BTreeNode) delete(key int, m int) {
    // 找到第一个不比key小的，注意leaf的数量比key数量多1
    idx := 0
    for idx < bTreeNode.keyNum && key > bTreeNode.keyList[idx] { // 这里可以采用二分查找提高效率
        idx++
    }
    curNode := bTreeNode.leafList[idx]

    if idx < bTreeNode.keyNum && bTreeNode.keyList[idx] == key {
        // 在当前节点找到了key
        bTreeNode.removeKey(idx)
    } else if curNode != nil {
        curNode.delete(key, m)
    }

    /**
    * 每一个非叶子节点（除根节点）最少有 ⌈m/2⌉ 个子节点
    * 有 k 个子节点的非叶子节点拥有 k − 1 个键
    * 因此非叶子结点最少有m/2个键
    **/
    // 叶子节点拥有的元素数量小于最低要求
    if curNode != nil && curNode.isLeaf && curNode.keyNum < m/2 { // 需要调整
        pos := idx
        if pos == 0 {
            pos = 1
        }
        leftBro := bTreeNode.leafList[pos-1]
        rightBro := bTreeNode.leafList[pos]
        if rightBro != nil && rightBro.keyNum > m/2 { // 父结点key并放到自己的最后 右兄弟的第一个key放到父结点
            // 如果缺少元素节点的右兄弟存在且拥有多余的元素，那么向左旋转
            bTreeNode.leftShift(idx)
        } else if leftBro != nil && leftBro.keyNum > m/2 { // 父结点key并放到自己的开头 左兄弟的最后一个key放到父结点
            // 如果缺少元素节点的左兄弟存在且拥有多余的元素，那么向右旋转
            bTreeNode.rightShift(idx)
        } else {
            // 如果它的两个直接兄弟节点都只有最小数量的元素，那么将它与一个直接兄弟节点以及父节点中它们的分隔值合并
            bTreeNode.merge(curNode, idx)
        }
    }
}

/**
* 删除key
* 时间复杂度O(logn)
**/
func (bTree *BTree) Delete(key int) {
    bTree.root.delete(key, bTree.m)
    // 父节点的元素数量小于最小值，重新平衡父节点
    if bTree.root.keyNum == 0 && bTree.root.leafList[0] != nil {
        bTree.root = bTree.root.leafList[0]
    }
}