数据结构之平衡二叉树（AVL树）

　　平衡二叉树(AVL树)定义如下：平衡二叉树或者是一棵空树，或者是具有以下性质的二叉排序树：

　　(1)它的左子树和右子树的高度之差绝对值不超过1；

　　(2)它的左子树和右子树都是平衡二叉树。

　　AVL树避免了平衡二叉树初始序列有序建立的类似单链表情况，提高了查找效率。

　　1.AVL树的相关参量定义

#define _CRT_SECURE_NO_DEPRECATE
#include<stdio.h>
#include<stdlib.h>
#include<windows.h>
#define DataType int
#define LH 1		//左边高一层
#define EH 0		//左右分支等高
#define RH -1		//右边高一层
const int MAXSIZE = 100;//栈和队列的最大容量
typedef struct BSTNode{
	DataType data;
	int bf;//平衡因子,值为LH、EH、RH
	struct BSTNode *lchild, *rchild;
}BSTNode, *BSTree;

　　2.插入函数

bool InsertAVL(BSTree &T,DataType x,boolean &taller)//插入后是否长高,一处修改处处修改，taller为bool类型
{//插入过程伴随着查找过程，没有则插入
	if (!T)//如果空树，则直接添加新结点
	{
		T = (BSTree)malloc(sizeof(BSTNode));
		T->data = x;
		T->lchild = T->rchild = NULL;
		T->bf = EH;
		taller = true;//长高了
	}
	else
	{
		if (T->data == x)//数据元素已存在，不必插入
		{
			taller = false;
			return false;
		}
		else if (x < T->data)//数据在树根的左分支
		{
			if (!InsertAVL(T->lchild, x, taller))//左分支已存在，但即使不存在也返回了taller的值
				return false;
			if (taller)//如果导致树长高了，则进一步判断及处理
			{
				switch (T->bf)
				{
					case LH://左分支本来就比右分支高一层，又加了一层，当然进行左平衡
						LeftBalence(T);//左调平衡函数
						taller = false;
						break;
					case EH://本来左右等高，修改标志位即可
						T->bf = LH;
						taller = true;
						break;
					case RH://本来右分支高1，修改标志位
						T->bf = EH;
						taller = false;
						break;
				}
			}
		}
		else
		{
			if (!InsertAVL(T->rchild, x, taller))//进行T的右分支，同理
				return false;
			if (taller)
			{
				switch (T->bf)
				{
					case RH:
						RightBalence(T);
						taller = false;
						break;
					case EH:
						T->bf = RH;
						taller = true;
						break;
					case LH:
						T->bf = EH;
						taller = false;
						break;
				}
			}
		}
	}
	return true;
}

　　3.着重分析左右调平衡函数

　　左调平衡

有且仅有两种情况，一定是原本左边比右边高1层，而且在左边加了1层才要左调平衡的。

（1）

　　　　　　　                    

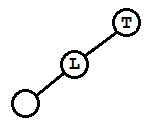
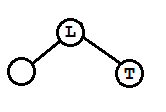
　　这种情况是在原本的根节点T的左孩子L上加了左孩子，显然此时T和L都无右孩子，所以要调整为L为根节点，也就是T根节点右旋（顺时针旋转）。

　　调整完显然平衡因子bf变化为  T->bf = L->bf = EH;

（2）另一种是在原本的根节点T的左孩子L上加了右孩子导致失衡（某一结点的做右分支高度相差大于1）产生。

（A）

　　　　　　 　     

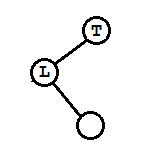
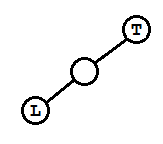
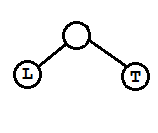
　　对应（1）的情况，在L加了右孩子Lr，且L无左孩子，T无右孩子。先将L左旋（L逆时针旋转）得到类似（1）的情形，然后将T右旋。

　　调整完三个结点平衡因子  T->bf = L->bf =Lr->bf= EH;

(B)此种情况为在L的右孩子Lr上加了左孩子

　　　　　  

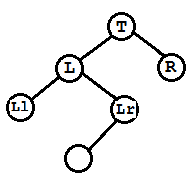
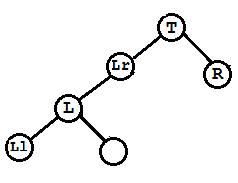
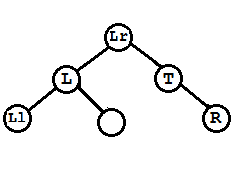
　　先将L左旋，Lr作为L的双亲结点T的左孩子，L作为Lr的左孩子，Lr的左孩子作为L的右孩子，这也是具体的左旋算法，然后将T右旋。

　　调整完三个结点平衡因子    T->bf = RH;   L->bf = EH;   Lr->bf = EH;

（C）此种情况为在L的右孩子Lr上加了右孩子

　　　　

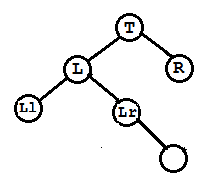
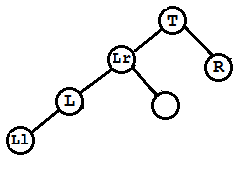
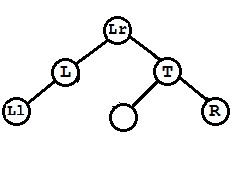
　　先将L左旋，然后将T作为Lr的右孩子，且将Lr的右孩子最为T的左孩子，这也是具体的右旋算法。

　　调整完三个结点平衡因子　T->bf = EH;  L->bf = LH; Lr->bf = EH;

　　注意，此调平衡的规则的代码是递归式的，所以一定是从底层往上层调平衡，也就是说下面先调平衡。

总结（2）：具体的也分析了左旋右旋的具体算法，每种情况都有Lr->bf=EH,并且算法都符合平衡二叉树的规则要求。

void R_Rotate(BSTree &T)//右旋，T的左孩子可能有右孩子或者为空，一起整
{
	BSTree p;
	p = T->lchild;
	T->lchild = p->rchild;
	p->rchild = T;
	T=p;
}
void L_Rotate(BSTree &T)//左旋
{
	BSTree p;
	p = T->rchild;
	T->rchild = p->lchild;
	p->lchild = T;
	T = p;
}
void LeftBalence(BSTree &T)//平衡左分支
{
	BSTree L, Lr;
	L = T->lchild;
	switch (L->bf)
	{
		case LH://是在根节点T的左孩子L的左孩子上加了结点导致失衡
			T->bf = L->bf = EH;//调整后的参数变化
			R_Rotate(T);//右旋根节点T
			break;
		case RH://是在根节点T的左孩子L的左孩子上加了结点导致失衡
			Lr = L->rchild;
			switch (Lr->bf)//对L的右孩子Lr的参数bf进行判断及进一步分析
			{
				case LH://Lr的左边加了新结点
					T->bf = RH;
					L->bf = EH;
					break;
				case EH://Lr左右等高
					T->bf = L->bf = EH;
					break;
				case RH://Lr的右边边加了新结点
					T->bf = EH;
					L->bf = LH;
					break;
			}
			//统一改参数，先左旋T的左孩子，再右旋T
			Lr->bf = EH;
			L_Rotate(T->lchild);
			R_Rotate(T);
	}
}

　　右调平衡与左调平衡类似的分析方法。

void RightBalence(BSTree &T)//平衡右分支
{
	BSTree R, Rl;
	R = T->rchild;
	switch (R->bf)
	{
		case RH:
			T->bf = R->bf = EH;
			L_Rotate(T);
			break;
		case LH:
			Rl = R->lchild;
			switch (Rl->bf)
			{
				case RH:
					T->bf = LH;
					R->bf = EH;
					break;
				case EH:
					T->bf = R->bf = EH;
					break;
				case LH:
					T->bf = EH;
					R->bf = RH;
					break;
			}
		Rl->bf = EH;
		R_Rotate(T->rchild);
		L_Rotate(T);
	}
}

　　4.创建函数及其他函数

void CreatAVL(BSTree &T,int n)//创建AVL树，用到了插入函数
{
	printf("请输入%d个数据：\n", n);
	int a;
	boolean taller = 0;//初始化
	for (int i = 0; i < n; i++)//循环添加
	{
		scanf("%d", &a);
		InsertAVL(T, a,taller);
	}
}
void InOrder(BSTree &T)//中序遍历看是否是递增序列
{
	if (T)
	{
		InOrder(T->lchild);
		printf("%3d", T->data);
		InOrder(T->rchild);
	}
}
void TreeDispNode(BSTree bt)//括号表示法，用来看树的构造情况
{
	if (bt != NULL)
	{
		printf("%d", bt->data);
		if (bt->lchild != NULL || bt->rchild != NULL)
		{
			printf("(");
			TreeDispNode(bt->lchild);
			if (bt->rchild != NULL)printf(",");
			TreeDispNode(bt->rchild);
			printf(")");
		}
	}
}

　　5.测试代码

int main()//测试代码
{
	BSTree mytree=NULL;
	CreatAVL(mytree, 10);
	InOrder(mytree);
	printf("\n");
	TreeDispNode(mytree);
	printf("\n");
	system("pause");
	return 0;
}

　　注意：代码的相关函数要调整位置，使得被调用的函数在调用其的函数之前，分析调整代码应数形结合。