ELBO 与 KL散度

浅谈KL散度

一、第一种理解　　

相对熵（relative entropy）又称为KL散度（Kullback–Leibler divergence，简称KLD），信息散度（information divergence），信息增益（information gain）。

　　KL散度是两个概率分布P和Q差别的非对称性的度量。

KL散度是用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的比特个数。 典型情况下，P表示数据的真实分布，Q表示数据的理论分布，模型分布，或P的近似分布。

根据shannon的信息论，给定一个字符集的概率分布，我们可以设计一种编码，使得表示该字符集组成的字符串平均需要的比特数最少。假设这个字符集是X，对x∈X，其出现概率为P(x)，那么其最优编码平均需要的比特数等于这个字符集的熵：

　　H(X)=∑_x∈XP(x)log[1/P(x)]

　　在同样的字符集上，假设存在另一个概率分布Q(X)。如果用概率分布P(X)的最优编码（即字符x的编码长度等于log[1/P(x)]），来为符合分布Q(X)的字符编码，那么表示这些字符就会比理想情况多用一些比特数。KL-divergence就是用来衡量这种情况下平均每个字符多用的比特数，因此可以用来衡量两个分布的距离。即：

　　D_KL(Q||P)=∑_x∈XQ(x)[log(1/P(x))] - ∑_x∈XQ(x)[log[1/Q(x)]]=∑_x∈XQ(x)log[Q(x)/P(x)]

　　由于-log(u)是凸函数，因此有下面的不等式

　　D_KL(Q||P) = -∑_x∈XQ(x)log[P(x)/Q(x)] = E[-logP(x)/Q(x)] ≥ -logE[P(x)/Q(x)] = -　　log∑_x∈XQ(x)P(x)/Q(x) = 0

　　即KL-divergence始终是大于等于0的。当且仅当两分布相同时，KL-divergence等于0。

　　===========================

　　举一个实际的例子吧：比如有四个类别，一个方法A得到四个类别的概率分别是0.1,0.2,0.3,0.4。另一种方法B（或者说是事实情况）是得到四个类别的概率分别是0.4,0.3,0.2,0.1,那么这两个分布的KL-Distance(A,B)=0.1*log(0.1/0.4)+0.2*log(0.2/0.3)+0.3*log(0.3/0.2)+0.4*log(0.4/0.1)

　　这个里面有正的，有负的，可以证明KL-Distance()>=0.

　　从上面可以看出， KL散度是不对称的。即KL-Distance(A,B)!=KL-Distance(B,A)

　　KL散度是不对称的，当然，如果希望把它变对称，

　　Ds(p1, p2) = [D(p1, p2) + D(p2, p1)] / 2.

二、第二种理解

　　今天开始来讲相对熵，我们知道信息熵反应了一个系统的有序化程度，一个系统越是有序，那么它的信息熵就越低，反之就越高。下面是熵的定义

如果一个随机变量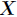的可能取值为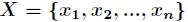，对应的概率为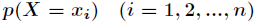，则随机变量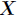的熵定义为

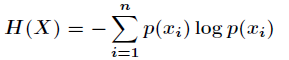
　　有了信息熵的定义，接下来开始学习相对熵。

　　1. 相对熵的认识

相对熵又称互熵，交叉熵，鉴别信息，Kullback熵，Kullback-Leible散度（即KL散度）等。设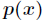和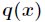

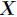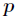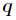是取值的两个概率概率分布，则对的相对熵为

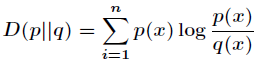
在一定程度上，熵可以度量两个随机变量的距离。KL散度是两个概率分布P和Q差别的非对称性的度量。KL散度是

用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下，P表示数据的真实分布，Q

表示数据的理论分布，模型分布，或P的近似分布。

2. 相对熵的性质

相对熵（KL散度）有两个主要的性质。如下

（1）尽管KL散度从直观上是个度量或距离函数，但它并不是一个真正的度量或者距离，因为它不具有对称性，即

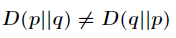
（2）相对熵的值为非负值，即

在证明之前，需要认识一个重要的不等式，叫做吉布斯不等式。内容如下

3. 相对熵的应用

相对熵可以衡量两个随机分布之间的距离，当两个随机分布相同时，它们的相对熵为零，当两个随机分布的差别增

大时，它们的相对熵也会增大。所以相对熵（KL散度）可以用于比较文本的相似度，先统计出词的频率，然后计算

KL散度就行了。另外，在多指标系统评估中，指标权重分配是一个重点和难点，通过相对熵可以处理。

4.交叉熵与相对熵

---

参考：http://www.cnblogs.com/hxsyl/p/4910218.html

https://www.zhihu.com/question/41252833

---

ELBO（证据下界）

网上关于ELBO的内容较少，主要常出现在变分推断当中。

例如在用EM处理LDA主题模型时，

看看文档数据的对数似然函数 如下，为了简化表示，用 代替 ，用来表示 对于变分分布 的期望。

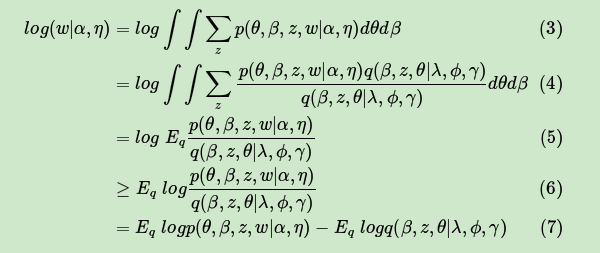
其中，从第(5)式到第(6)式用到了Jensen不等式：

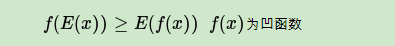
一般把第(7)式记为：

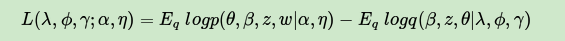
由于 是我们的对数似然的一个下界（第6式），所以这个L一般称为ELBO(Evidence Lower BOund)。那么这个ELBO和我们需要优化的的KL散度有什么关系呢？注意到：

在(10)式中，由于对数似然部分和我们的KL散度无关，可以看做常量，因此我们希望最小化KL散度等价于最大化ELBO。那么我们的变分推断最终等价的转化为要求ELBO的最大值。现在我们开始关注于极大化ELBO并求出极值对应的变分参数λ,ϕ,γ。

---

参考文献：https://zhuanlan.zhihu.com/p/29932017