day-13 python库实现简单非线性回归应用

一、概率

　　在引入问题前，我们先复习下数学里面关于概率的基本概念

　　概率：对一件事发生的可能性衡量

　　范围：0<=P<=1

　　计算方法：根据个人置信区间；根据历史数据；根据模拟数据。

　　条件概率：B发生的条件下，A发生的概率

　　

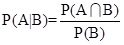
二、Logistic Regression（逻辑回归）

1、问题引入

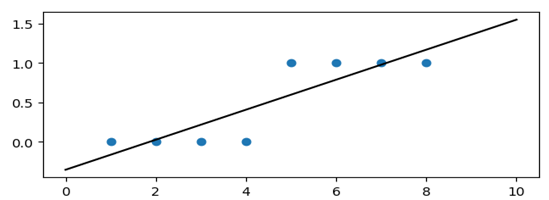
　　处理二值数据时，如果一直8个测试数据集为如下所示，我们利用线性回归方程，建立回归方程曲线，图形显示，并不能很好的模拟回归问题，也就是我们所说的欠回归。

　　

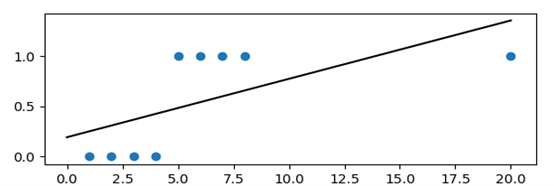
　　如果继续引入第9个测试点，我们发现欠回归情况更加严重，因此我们需要引入一个新的回归模型，来解决该类模型欠回归问题。

　　

2、简单推导过程

　　假设测试数据为X（x0，x1，x2···xn）

　　要学习的参数为：Θ（θ0，θ1，θ2，···θn）

向量表示：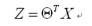

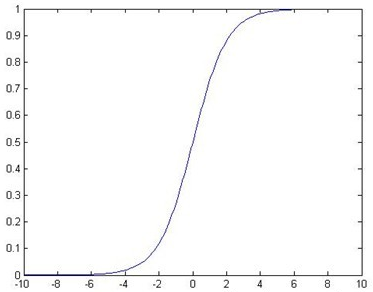
　　观察Logistic函数曲线，我们发现在0到负无穷时，函数值趋向于0，0到正无穷时函数曲线趋向于1，且当z等于0时，函数值为0.5，于是我们可以引入该函数，对预测方程进行再次转换，由数值上的计算转换为0，1概率上的计算，即：

　　

　　

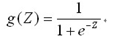
不同于线性回归模型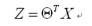：，定义一个新的预测函数为：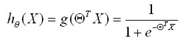

　　于是问题从对Z函数求最优theta参数值，变为对h函数求最优theta参数值。对二值问题，可转换为如下表述：

　　

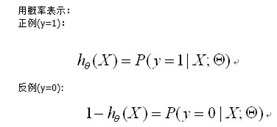
根据一般方法，首先定义新的cost函数，然后根据cost函数来反向更新参数theta值，如下为新的cost函数：

　　

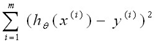
为了计算方便，我们对其转化为：

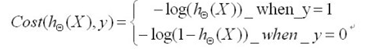
两个式子可以进行合并，最终化简为最终的cost函数：

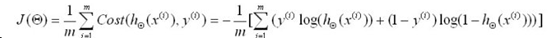
该式为非线性方程，通过求导来计算极值很复杂，我们引入之前的梯度下降算法，来不断的估计新的参数值

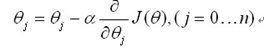
最终更新法则为：

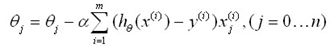
3、实际编程应用

　　如下为一个通用的非线性回归方程，在利用梯度下降算法反向更新theta参数值时，没有使用如下更新法则，而是使用通用方法，如下是具体代码：

　　

import numpy as np
import random

# 梯度下降算法来更新参数值
# x,y:测试数据集及标签值，theta:学习的参数值，alpha：学习率，m：测试数据集个数，numIterations：重复更新次数
def gradientDescent(x,y,theta,alpha,m,numIterations):
    xTrans = np.transpose(x)
    for i in range(0,numIterations):
        hypothesis = np.dot(x,theta)
        loss = hypothesis - y
        # 定义一个通用的更新法则7
        cost = np.sum(loss**2)/(2*m)
        if i % 10000 == 0:
            print("Iteration %d | Cost:%f"%(i,cost))
        gradient = np.dot(xTrans,loss)/m
        theta = theta - alpha*gradientreturn theta

# 生成测试数据
# numPoints:测试数据集行数，bias:偏向，variance:方差
def genData(numPoints,bias,variance):
    x = np.zeros(shape=(numPoints,2))
    y = np.zeros(shape=numPoints)
    for i in range(0,numPoints):
        x[i][0] = 1
        x[i][1] = i
        # uniform随机产生一些数字
        y[i] = (i + bias) + random.uniform(0,1) + variance
    return x,y

x,y = genData(100,25,10)
m,n = np.shape(x)
print(x,y)
theta = np.ones(n)
alpha = 0.0005
theta = gradientDescent(x,y,theta,alpha,m,100000)
print(theta)

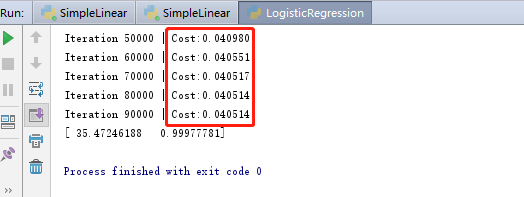
　　最终的结果如下，结果显示，随着训练次数的增加，目标函数也在不断的减小：