数字电路基础（二）TTL与非门输入端悬空和接大电阻的问题

引言

我们在做那些判断与非门输入输出的时候，常常把输入端悬空和接大电阻作为高电平输入处理，比如下边这一例题：

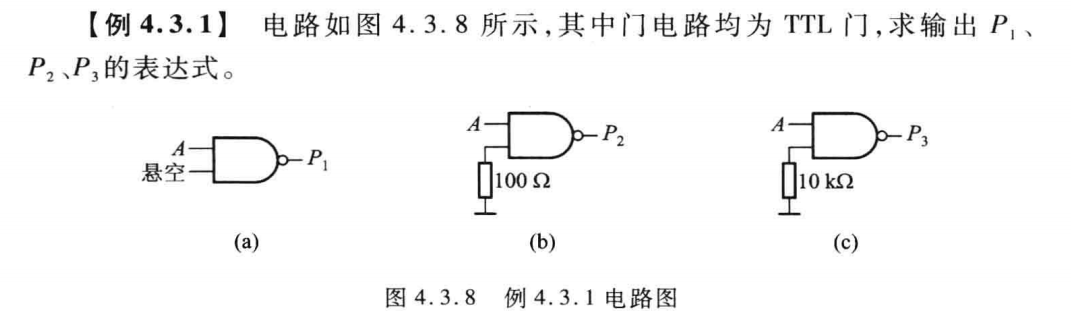
很显然，我们无法直接从与非门逻辑图中看出其内部工作原理，那我们该如何分析呢？那肯定是去分析电路的输入负载特性曲线了。如下图所示：

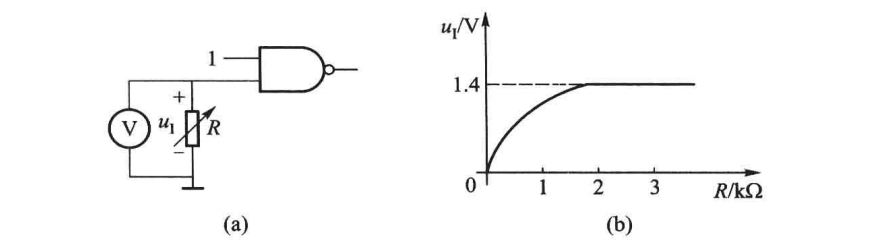
其中R表示输入端接入的负载，u_i表示负载上降落的电压，也表示与非门其中一端的输入电压。

分析一：

如图所示，在输入端口B处接一个电阻R，则Vcc，R1，VT1的基极与集电极和R构成一个回路，此时电阻R两端的电压可以表示为：U=R/(R+R1) * (Vcc-0.7)。可见，当其余值都确定的时候，电阻值越大，输入电压越大。

此处也存在着一个关门电阻R_off，即R两端的压降达到输出高电平最小值对应的输入电压。我们也可以认为当输入端接的电阻小于R_off的时候输入表现为低电平。

分析二

但是当输入电压增大至2.1v的时候，VT2和VT5都导通，此时的VT1的电位被钳位到2.1v不再变化，那么电阻R两端的电压就是2.1-0.7=1.4（v）左右了，且不再增加。

此处也存在着一个开门电阻R_on，即R两端的压降达到输出低电平最大值对应的输入电压。我们也可以认为当输入端接的电阻大于R_on的时候输入表现为高电平。

而对于悬空来说，我们可以理解为电阻是无穷大的状态 ，此时电流流向VT2和VT，只要电路的参数正确，VT2和VT5都导通，输出低电平

另外，对于cmos与非门来说，无论接的电阻多大，都是表现为逻辑0.