BP神经网络
秋招刚结束,这俩月没事就学习下斯坦福大学公开课,想学习一下深度学习(这年头不会DL,都不敢说自己懂机器学习),目前学到了神经网络部分,学习起来有点吃力,把之前学的BP(back-progagation)神经网络复习一遍加深记忆。看了许多文章发现一PPT上面写的很清晰,就搬运过来,废话不多说,直入正题:
单个神经元
神经网络是由多个“神经元”组成,单个神经元如下图所示:
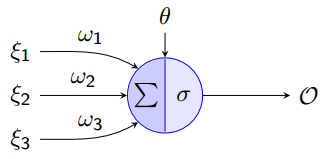
这其实就是一个单层感知机,输入是由ξ1 ,ξ2 ,ξ3和Θ组成的向量。其中Θ为偏置(bias),σ为激活函数(transfer function),本文采用的是sigmoid函数 ,功能与阶梯函数(step function)相似控制设神经元的输出,它的优点是连续可导。
,功能与阶梯函数(step function)相似控制设神经元的输出,它的优点是连续可导。
 是神经元的输出,结果为
是神经元的输出,结果为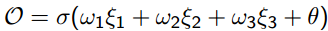
可以看得出这个“神经元”的输入-输出映射其实就是一个逻辑回归,常用的激活函数还有双曲正切函数 。
激活函数
sigmoid:函数

取值范围为[0,1],它的图像如下:
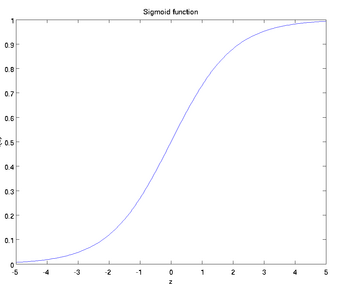
求导结果为:

tanh函数:
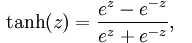
取值范围为[-1,1],图像如下:
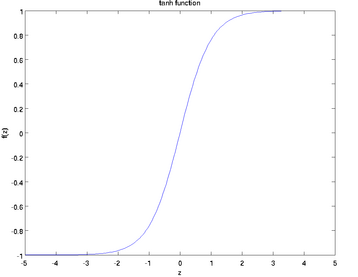
求导数结果为 。本文采用的是sigmoid函数作为激活函数。
。本文采用的是sigmoid函数作为激活函数。
神经网络模型
神经网络将许多“神经元”联结在一起,一个神经元的输出可以是另一个“神经元”的输入,神经元之间的传递需要乘法上两个神经元对应的权重,下图就是一个简单的神经网络:
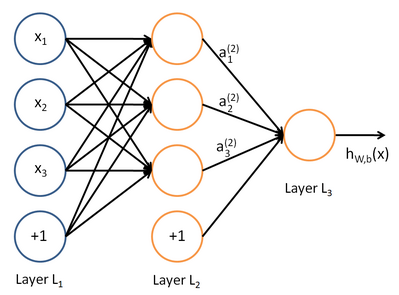
这是一个三层的神经网络,使用圆圈来表示神经元的输入,“+1”被称为偏置节点,从左到右依次为输入层、隐藏层和输出层,从图中可以看出,有3个输入节点、3个隐藏节点和一个输出单元(偏置不接受输入)。
本例神经网络的参数有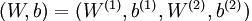 ,其中
,其中 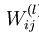 是第l层第 j 单元与 l+1层第
是第l层第 j 单元与 l+1层第  单元之间的联接参数,即:节点连线的权重,本图中
单元之间的联接参数,即:节点连线的权重,本图中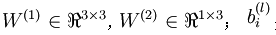 是第l+1 层第i单元的偏置项。
是第l+1 层第i单元的偏置项。
向前传播
机器学习(有监督)的任务无非是损失函数最小化,BP神经网络的原理是前向传播得到目标值(分类),再通过后向传播对data loss进行优化求出参数。可见最优化部分
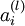 表示
表示 层第
层第  单元激活值(输出值)。当
单元激活值(输出值)。当 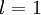 时,
时, 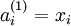 ,也就是第
,也就是第  个输入值。对于给定参数集
个输入值。对于给定参数集 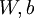 ,
,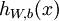 来表示神经网络最后计算输出的结果。上图神经网络计算步骤如下:
来表示神经网络最后计算输出的结果。上图神经网络计算步骤如下:
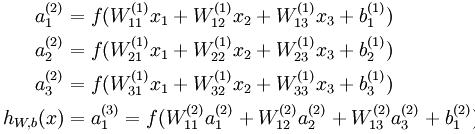
可以看出,神经网络的核心思想是这一层的输出乘上相应的权重加上偏置,带入激活函数后的输出又是下一层的输入。用 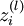 表示第
表示第 层第
层第 单元输入加权和
单元输入加权和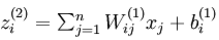 ,则
,则 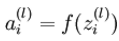 。使用向量化表示方法表示,上面的公式可以简写为:
。使用向量化表示方法表示,上面的公式可以简写为:

这些计算步骤就是前向传播,将计算过程进行推广,给定第  层的激活值
层的激活值 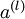 ,第
,第  层的激活值
层的激活值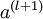 的计算过程为:
的计算过程为:
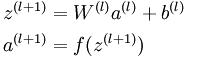
反向传播
在前向传播中,我们得到了神经网络的预测值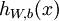 ,这时候可以通过反向传播的方法计算出参数
,这时候可以通过反向传播的方法计算出参数
符号定义
 :第l层第j个节点的输入。
:第l层第j个节点的输入。
 :从第l-1层第i个节点到第l层第j个节点的权值。
:从第l-1层第i个节点到第l层第j个节点的权值。
 :Sigmoid激活函数。
:Sigmoid激活函数。
 ::第l层第j个节点的偏置。
::第l层第j个节点的偏置。
 ::第l层第j个节点的输出。
::第l层第j个节点的输出。
 ::输出层第j个节点的目标值(label)。
::输出层第j个节点的目标值(label)。
使用梯度下降的方法求解参数,在求解的过程中需要对输出层和隐藏层分开计算
输出层权重计算
给定样本标签 和模型输出结果
和模型输出结果 ,输出层的损失函数为:
,输出层的损失函数为:

这其实就是均方差项,训练的目标是最小化该误差,使用梯度下降方法进行优化,对上式子对权重W进行求导:

,整理 ,
,
其中 =
= 带入
带入 ,对sigmoid求导得:
,对sigmoid求导得:

输出层第k个节点的输入 等于上一层第j个节点的输出
等于上一层第j个节点的输出 乘上
乘上 ,即
,即 =
=
 ,而上一层的输出
,而上一层的输出 与输出层的权重变量
与输出层的权重变量 无关,可以看做一个常数,所以直接求导可以得到:
无关,可以看做一个常数,所以直接求导可以得到:
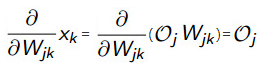
所以将 =
= 带入式子中就得到:
带入式子中就得到:

为了方便表示将上式子记作:

其中:

隐藏层权重计算
采用同样方法对隐藏层的权重进行计算,与前面不同的是关于隐藏层和前一层权重的调整

整理

替换sigmoid函数

对sigmoid求导

把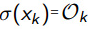 带入进去,使用求导的链式法则:
带入进去,使用求导的链式法则:

输出层的输入等于上一层的输入乘以相应的权重,即: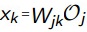 于是得到
于是得到

对 进行求导(
进行求导( =
= ,同样适用于j),
,同样适用于j),

同输出层计算的方法一样,再次利用 ,j换成i,k换成j同样成立,带入进去:
,j换成i,k换成j同样成立,带入进去:

整理,得到:

其中:
我们还可以仿照 的定义来定义一个
的定义来定义一个 ,得到:
,得到:

其中:
偏置调整
从上面的计算步骤中可以看出:例如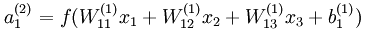 ,偏置节点是不存在对应的权值参数,也就是不存在关于权值变量的偏导数。
,偏置节点是不存在对应的权值参数,也就是不存在关于权值变量的偏导数。
对偏置直接求导:

又有

得到:
 ,其中:
,其中:
BP算法步骤
1. 随机初始化W和b,需要注意的是,随机初始化并是不是全部置为0,如果所有参数都是用相同的值初始化,那么所有隐藏单元最终会得到与输入值相关、相同的函数(也就是说,对于所有  ,
,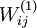 都会取相同的值,那么对于任何输入
都会取相同的值,那么对于任何输入  都会有:
都会有: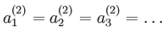 ),随机初始化的目的是使对称失效。
),随机初始化的目的是使对称失效。
2.对每个输出节点按照这个公式计算delta:

3.对每个隐藏节点按照这个公式计算delta:

4.更新W和b的公式为:

并更新参数 ,这里的η是学习率。
,这里的η是学习率。
Reference
2.反向传导算法
BP神经网络的更多相关文章
- BP神经网络原理及python实现
[废话外传]:终于要讲神经网络了,这个让我踏进机器学习大门,让我读研,改变我人生命运的四个字!话说那么一天,我在乱点百度,看到了这样的内容: 看到这么高大上,这么牛逼的定义,怎么能不让我这个技术宅男心 ...
- 数据挖掘系列(9)——BP神经网络算法与实践
神经网络曾经很火,有过一段低迷期,现在因为深度学习的原因继续火起来了.神经网络有很多种:前向传输网络.反向传输网络.递归神经网络.卷积神经网络等.本文介绍基本的反向传输神经网络(Backpropaga ...
- BP神经网络推导过程详解
BP算法是一种最有效的多层神经网络学习方法,其主要特点是信号前向传递,而误差后向传播,通过不断调节网络权重值,使得网络的最终输出与期望输出尽可能接近,以达到训练的目的. 一.多层神经网络结构及其描述 ...
- 极简反传(BP)神经网络
一.两层神经网络(感知机) import numpy as np '''极简两层反传(BP)神经网络''' # 样本 X = np.array([[0,0,1],[0,1,1],[1,0,1],[1, ...
- BP神经网络
BP神经网络基本原理 BP神经网络是一种单向传播的多层前向网络,具有三层或多层以上的神经网络结构,其中包含输入层.隐含层和输出层的三层网络应用最为普遍. 网络中的上下层之间实现全连接,而每层神经元之 ...
- BP神经网络学习笔记_附源代码
BP神经网络基本原理: 误差逆传播(back propagation, BP)算法是一种计算单个权值变化引起网络性能变化的较为简单的方法.由于BP算法过程包含从输出节点开始,反向地向第一隐含层(即最接 ...
- 机器学习(一):梯度下降、神经网络、BP神经网络
这几天围绕论文A Neural Probability Language Model 看了一些周边资料,如神经网络.梯度下降算法,然后顺便又延伸温习了一下线性代数.概率论以及求导.总的来说,学到不少知 ...
- 基于Storm 分布式BP神经网络,将神经网络做成实时分布式架构
将神经网络做成实时分布式架构: Storm 分布式BP神经网络: http://bbs.csdn.net/topics/390717623 流式大数据处理的三种框架:Storm,Spark和Sa ...
- BP神经网络算法学习
BP(Back Propagation)网络是1986年由Rumelhart和McCelland为首的科学家小组提出,是一种按误差逆传播算法训练的多层前馈网络,是眼下应用最广泛的神经网络模型之中的一个 ...
随机推荐
- DynamicJson
json字符串解析成Dynamic对象,开源地址http://dynamicjson.codeplex.com/,访问比较慢.使用方法摘录如下: Project Descriptiondynamic ...
- 深入理解iOS开发中的BitCode功能
前言 做iOS开发的朋友们都知道,目前最新的Xcode7,新建项目默认就打开了bitcode设置.而且大部分开发者都被这个突如其来的bitcode功能给坑过导致项目编译失败,而这些因为bitcode而 ...
- java连接sql问题
1.No suitable driver found for Jdbc: 1)确保jdbc:sqlserver://localhost;user=sa;password=123456;databas ...
- html、css基础注意点
之前第一次接触html,一直使用table进行布局,十分麻烦还相当丑陋,造成当初并没有多大的兴趣,直到半年前开始接触到了使用div+css编写页面,才对它有了兴趣.作为一个菜鸟记录自己的点滴教训与收获 ...
- 基础篇-Windows保护模式
1 一般来说,80x86(80386及其以后的各代CPU)可以在三种模式下运转:实模式,保护模式,V86模式.实模式就是古老的MS-DOS的运行环境.Win95只利用了两种模式:保护模式和V86模式. ...
- LeetCode 201 Bitwise AND of Numbers Range 位运算 难度:0
https://leetcode.com/problems/bitwise-and-of-numbers-range/ [n,m]区间的合取总值就是n,m对齐后前面一段相同的数位的值 比如 5:101 ...
- NOIP2016之反面教材提供
NOIP 2016信息竞赛总结 竞赛历程总结: 算下来一共学了11个月的信息竞赛,从最初进来的时候大概会一点最最基础的语法,上课什么也听不懂,然后一直追进度,我想在这个阶段中我的问题主要是自己知道自己 ...
- Android studio打开之后 cannot load project: java.lang.NUllpointerException
参考来源:http://bbs.csdn.net/topics/391014393 关闭网络,重新打开Android studio就好了.(但是原因不清楚是为什么?) Internal error. ...
- Add listitem with javascript 分类: Sharepoint 2015-07-16 20:23 4人阅读 评论(0) 收藏
SP.SOD.executeFunc('sp.js', 'SP.ClientContext', createListItem);//makes sure sp.js is loaded and the ...
- golang实现随机数
package main import ( "fmt" "time" "math/rand" ) func main() { r := ra ...
