深度学习常见的优化方法(Optimizer)总结:Adam,SGD,Momentum,AdaGard等

机器学习的常见优化方法在最近的学习中经常遇到，但是还是不够精通．将自己的学习记录下来，以备不时之需

基础知识:

机器学习几乎所有的算法都要利用损失函数 lossfunction 来检验算法模型的优劣，同时利用损失函数来提升算法模型．

这个提升的过程就叫做优化(Optimizer)

下面这个内容主要就是介绍可以用来优化损失函数的常用方法

常用的优化方法(Optimizer):

• 1.SGD&BGD&Mini-BGD:
  
  SGD(stochastic gradient descent):随机梯度下降,算法在每读入一个数据都会立刻计算loss function的梯度来update参数．假设loss function为L(w)，下同．\[w-=\eta \bigtriangledown_{w_{i}}L(w_{i}) \]
  
  Pros:收敛的速度快；可以实现在线更新；能够跳出局部最优
  
  Cons:很容易陷入到局部最优，困在马鞍点．
  
  BGD(batch gradient descent):批量梯度下降，算法在读取整个数据集后累加来计算损失函数的的梯度
  \[w-=\eta \bigtriangledown_{w}L(w)\]
  
  Pros:如果loss function为convex，则基本可以找到全局最优解
  
  Cons:数据处理量大，导致梯度下降慢;不能实时增加实例，在线更新；训练占内存
  
  Mini-BGD(mini-batch gradient descent):顾名思义，选择小批量数据进行梯度下降，这是一个折中的方法．采用训练集的子集(mini-batch)来计算loss function的梯度．\[w-=\eta \bigtriangledown_{w_{i:i+n}}L(w_{i:i+n})\]
  
  这个优化方法用的也是比较多的，计算效率高而且收敛稳定，是现在深度学习的主流方法．

  上面的方法都存在一个问题，就是update更新的方向完全依赖于计算出来的梯度．很容易陷入局部最优的马鞍点．能不能改变其走向，又保证原来的梯度方向．就像向量变换一样，我们模拟物理中物体流动的动量概念(惯性).引入Momentum的概念．

• 2.Momentum
  
  在更新方向的时候保留之前的方向，增加稳定性而且还有摆脱局部最优的能力\[\Delta w=\alpha \Delta w- \eta \bigtriangledown L(w)\] \[w=w+\Delta w\]
  
  若当前梯度的方向与历史梯度一致（表明当前样本不太可能为异常点），则会增强这个方向的梯度，若当前梯度与历史梯方向不一致，则梯度会衰减。一种形象的解释是：我们把一个球推下山，球在下坡时积聚动量，在途中变得越来越快，\(\eta\)可视为空气阻力，若球的方向发生变化，则动量会衰减。
• 3.Adagrad：(adaptive gradient)自适应梯度算法,是一种改进的随机梯度下降算法．
  以前的算法中，每一个参数都使用相同的学习率\(\alpha\). Adagrad算法能够在训练中自动对learning_rate进行调整，出现频率较低参数采用较大的\(\alpha\)更新．出现频率较高的参数采用较小的\(\alpha\)更新．根据描述这个优化方法很适合处理稀疏数据．\[G=\sum ^{t}_{\tau=1}g_{\tau} g_{\tau}^{T} 　其中 s.t. g_{\tau}=\bigtriangledown L(w_{i})\] 对角线矩阵\[G_{j,j}=\sum _{\tau=1}^{t} g_{\tau,j\cdot}^{2}\] 这个对角线矩阵的元素代表的是参数的出现频率.每个参数的更新\[w_{j}=w_{j}-\frac{\eta}{\sqrt{G_{j,j}}}g_{j}\]
• 4.RMSprop:(root mean square propagation)也是一种自适应学习率方法．不同之处在于，Adagrad会累加之前所有的梯度平方，RMProp仅仅是计算对应的平均值．可以缓解Adagrad算法学习率下降较快的问题．\[v(w,t)=\gamma v(w,t-1)+(1-\gamma)(\bigtriangledown L(w_{i}))^{2} ,其中 \gamma 是遗忘因子\]　　参数更新\[w=w-\frac{\eta}{\sqrt{v(w,t)}}\bigtriangledown L(w_{i})\]

• 5.Adam:(adaptive moment estimation)是对RMSProp优化器的更新.利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率.
  优点:每一次迭代学习率都有一个明确的范围,使得参数变化很平稳.
  \[m_{w}^{t+1}=\beta_{1}m_{w}^{t}+(1-\beta_{1}) \bigtriangledown L^{t} ,m为一阶矩估计\]
  \[v_{w}^{t+1}=\beta_{2}m_{w}^{t}+(1-\beta_{2}) (\bigtriangledown L^{t})^{2},v为二阶矩估计\]
  \[\hat{m}_{w}=\frac{m_{w}^{t+1}}{1-\beta_{1}^{t+1}}，估计校正，实现无偏估计\]
  \[\hat{v}_{w}=\frac{v_{w}^{t+1}}{1-\beta_{2}^{t+1}}\]
  \[w^{t+1} \leftarrow=w^{t}-\eta \frac{\hat{m}_{w}}{\sqrt{\hat{v}_{w}}+\epsilon}\]
  Adam是实际学习中最常用的算法

优化方法在实际中的直观体验

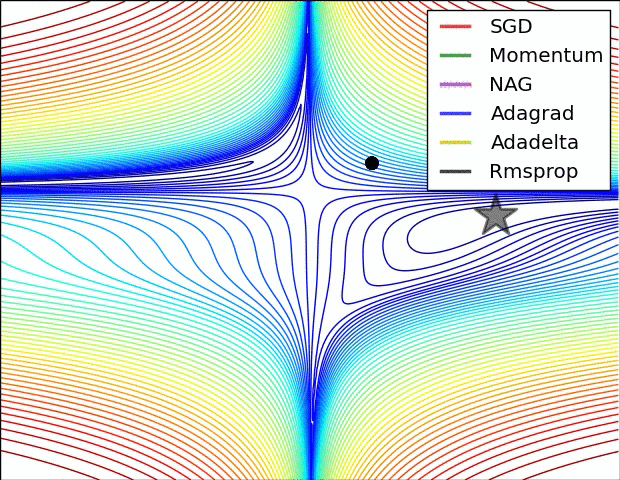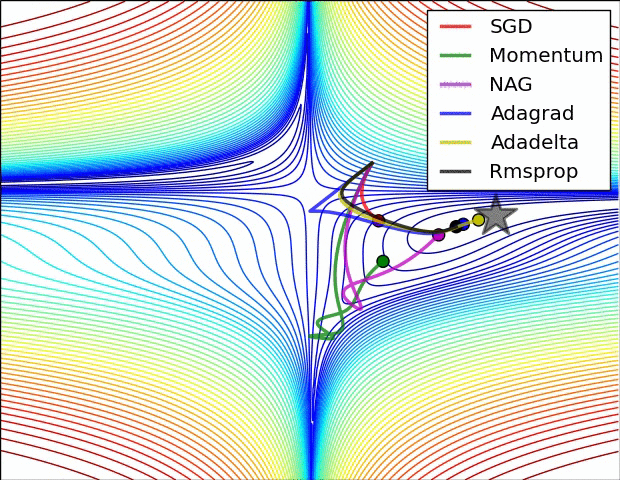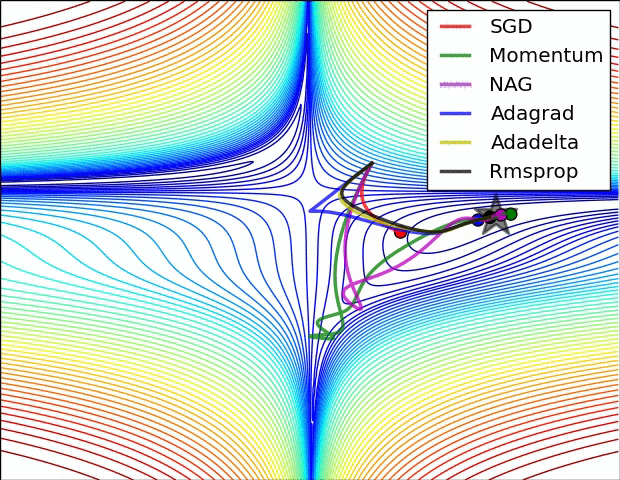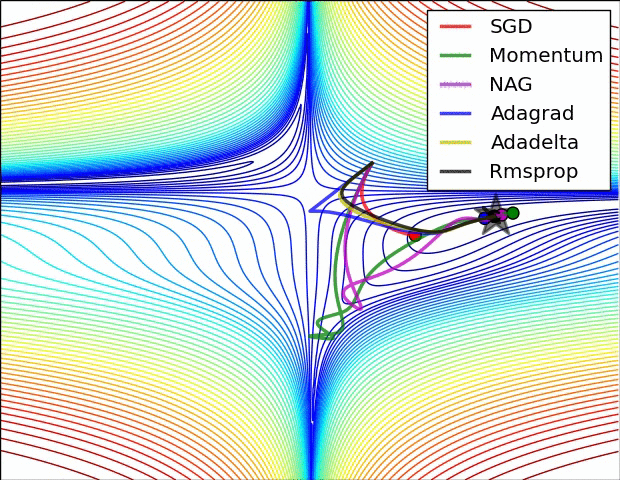
损失曲面的轮廓和不同优化算法的时间演化。 注意基于动量的方法的“过冲”行为，这使得优化看起来像一个滚下山的球

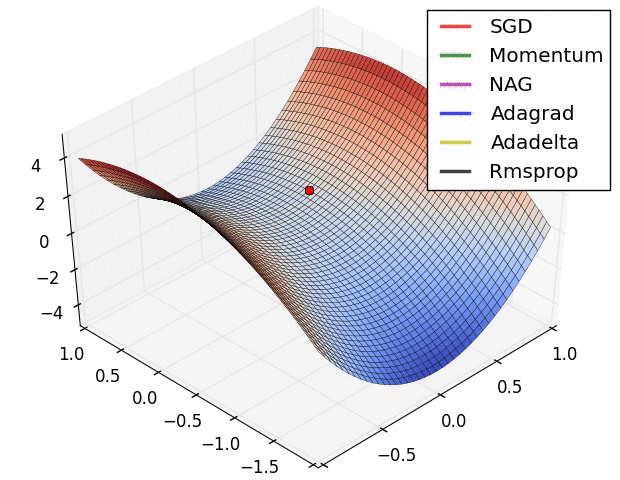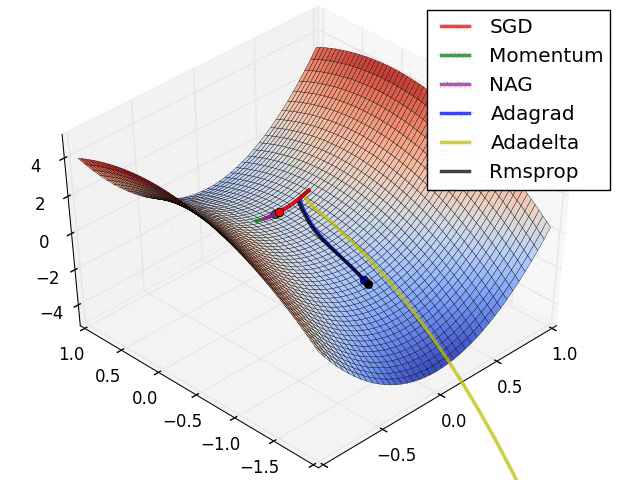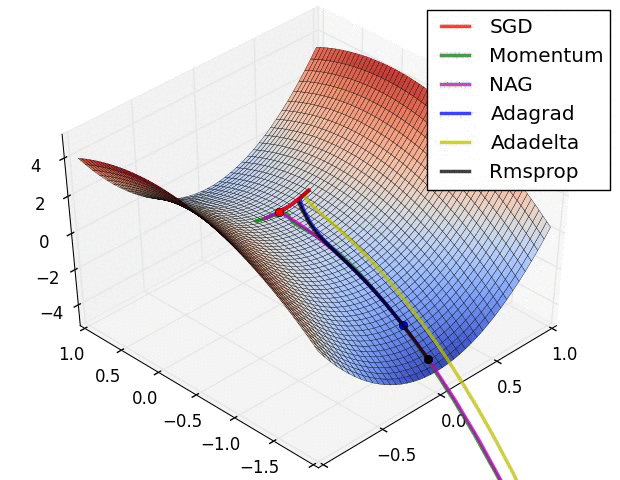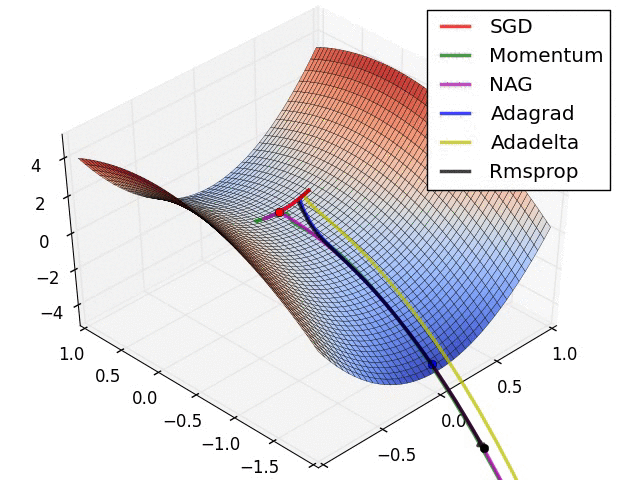
优化环境中鞍点的可视化，其中沿不同维度的曲率具有不同的符号（一维向上弯曲，另一维向下）。 请注意，SGD很难打破对称性并陷入困境。 相反，诸如RMSprop之类的算法将在鞍座方向上看到非常低的梯度。 由于RMSprop更新中的分母术语，这将提高此方向的有效学习率，从而帮助RMSProp继续进行.

参考文献：

• wiki-Stochastic gradient descent
• cs231n-lecture6,notes3:Parameter updates