P3376 网络最大流模板（Dinic + dfs多路增广优化 + 炸点优化 + 当前弧优化）

### P3376 题目链接 ###

这里讲一下三种优化的实现以及正确性。

1、dfs多路增广优化

一般的Dinic算法中是这样的，bfs() 用于标记多条增广路，以至于能一次 bfs() 出多次 dfs()增广路。那么就会有 while（bfs()） 一次，然后 dfs() n 次，出 n 条增广路。

那么我们 dfs 的优化在于使得一次 dfs() 直接累加出这一次 bfs() 所标记出的 n 条增广路。变成 while（bfs()）然后 dfs() 一次 即可。

一般的 Dinic 算法：

int dfs(int u,int res)
{
    if(u==T) return res;
    for(int i=head[u];i!=-;i=edge[i].next){
        int v=edge[i].to;
        if(flag[v]==flag[u]+&&edge[i].val){
            if(int k=dfs(v,min(res,edge[i].val))){
                edge[i].val-=k;
                edge[i^].val+=k;
                return k;
            }
        }
    }
    return ;
}

这里的 return k 保证了每次 dfs() 到达终点 T 时，出一次增广路的流量 k ，然后就返回结束了这次 dfs() 。

那我们需要做的是，使得 dfs() 搜到所有 增广路 后才 return 。

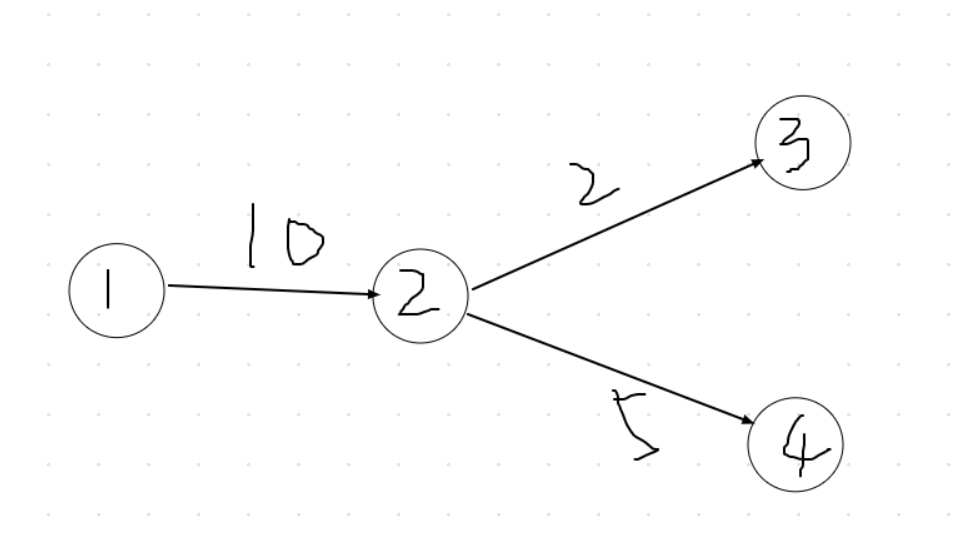
那么可以这样，我们用 nowflow 表示当前点所经历过的流量。我们看下图，比如现在 u == 2 时，1---> 2 的流量限制为 10 ，那么在每次返回到 u 点时，u 点所能经过的流量不能大于 10 ，否则这条路将不会成为增广路。那么用 nowflow 来累加出 u 点的流量，一旦 nowflow 等于 10 ，则增广路将无法再从 u 点伸展，故 break 即可。

对于 min 中的 flow - nowflow ，这里是为了告诉 u 后面的所有点的总流量不能大于 flow - nowflow ，即 u 点所能承载的最大流量。

然后对于返回值的问题：需要返回该点的流量。原因是因为，如果该点被伸展完后，那么一直返回该点的流量，直到返回到起点 S 的 nowflow 值为 0  ，则此时的 nowflow 就表示这次 bfs() 所能找到的所有增广路的流量和。

int dfs(int u,int flow)
{
    int nowflow=;
    if(u==T) return flow;
    for(int i=head[u];i!=-;i=edge[i].next){
        cur[u]=i;
        int v=edge[i].to;
        if(d[v]==d[u]+&&edge[i].val>){
            if(int k=dfs(v,min(flow-nowflow,edge[i].val))){
                edge[i].val-=k;
                edge[i^].val+=k;
                nowflow+=k;
                if(nowflow==flow) break;
            }
        }
    }
    return nowflow;//这里需要返回该点的总流量
}

2、炸点优化

如果当前 u 点伸展完后发现过这个点没有任何增广路被发现，即当前点 nowflow ，则说明增广路不可能通过该点伸展，故直接把这个点 “炸” 掉，即 d[u] = -1 。

int dfs(int u,int flow)
{
    int nowflow=;
    if(u==T) return flow;
    for(int i=head[u];i!=-;i=edge[i].next){
        cur[u]=i;
        int v=edge[i].to;
        if(d[v]==d[u]+&&edge[i].val>){
            if(int k=dfs(v,min(flow-nowflow,edge[i].val))){
                edge[i].val-=k;
                edge[i^].val+=k;
                nowflow+=k;
                if(nowflow==flow) break;
            }
        }
    }
    if(!nowflow) d[u]=-; // 炸点
    return nowflow;
}

3、当前弧优化

对于一次 bfs() 后寻找增广路来说，在 dfs() 时如果询问了一条路的编号为 a 时，那么不再会通过这条路增广。

比如这里一开始已经通过 1 → 2 → 3 进行了增广，流量累加了。那么下次再遍历到 点 2 时，2 → 3 这条路是不会再提供流量的，所以可以直接排除掉（当然它可能走 3 → 2 这条相应的反向边，反正边的 id 不一样，没影响）

这样我们用 cur[u] 来表示当前 u 点所延伸到的最后一个边的序号，然后下次遍历到 u 点时，直接从这条边开始遍历。

int dfs(int u,int flow)
{
    int nowflow=;
    if(u==T) return flow;
    for(int i=cur[u];i!=-;i=edge[i].next){
        cur[u]=i; // 当前弧优化
        int v=edge[i].to;
        if(d[v]==d[u]+&&edge[i].val>){
            if(int k=dfs(v,min(flow-nowflow,edge[i].val))){
                edge[i].val-=k;
                edge[i^].val+=k;
                nowflow+=k;
                if(nowflow==flow) break;
            }
        }
    }
    if(!nowflow) d[u]=-;
    return nowflow;
}

这三种优化会使得Dinic时间复杂度降低很多，这边测试是直接降了接近 300 MS 。

总代码如下：

#define IO freopen("test.in","r",stdin),freopen("test.out","w",stdout)
#define inf 0x3f3f3f3f
#define lson root<<1
#define rson root<<1|1
#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <cassert>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define maxn 10008
#define inf 0x3f3f3f3f
int N,M,S,T,cnt;
int head[maxn],cur[maxn],d[maxn];
inline int read()
{
    int x=,w=;char ch=;
    while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
    while(isdigit(ch)){x=(x<<)+(x<<)+(ch^);ch=getchar();}
    return w?-x:x;
}
struct Edge
{
    int to;
    int val;
    int next;
}edge[];
inline void add(int u,int v,int w)
{
    edge[++cnt].to=v;
    edge[cnt].val=w;
    edge[cnt].next=head[u];
    head[u]=cnt;
    return;
}
bool bfs()
{
    queue<int> q;
    while(!q.empty()) q.pop();
    for(int i=;i<=N;i++) d[i]=-;
    d[S]=;
    q.push(S);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i!=-;i=edge[i].next){
            int v=edge[i].to;
            if(d[v]==-&&edge[i].val>){
                d[v]=d[u]+;
                q.push(v);
            }
        }
    }
    return d[T]!=-;
}
int dfs(int u,int flow)
{
    int nowflow=;
    if(u==T) return flow;
    for(int i=cur[u];i!=-;i=edge[i].next){
        cur[u]=i;
        int v=edge[i].to;
        if(d[v]==d[u]+&&edge[i].val>){
            if(int k=dfs(v,min(flow-nowflow,edge[i].val))){
                edge[i].val-=k;
                edge[i^].val+=k;
                nowflow+=k;
                if(nowflow==flow) break;
            }
        }
    }
    if(!nowflow) d[u]=-;
    return nowflow;
}
int Dinic()
{
    int ans=;
    while(bfs())
    {
        for(int i=;i<=N;i++) cur[i]=head[i];
        ans+=dfs(S,inf);
    }
    return ans;
}
int main()
{
    //IO;
    N=read(),M=read(),S=read(),T=read();
    int A,B,C;
    cnt=-;
    for(int i=;i<=N;i++) head[i]=-;
    while(M--)
    {
        A=read(),B=read(),C=read();
        add(A,B,C),add(B,A,);
    }
    printf("%d\n",Dinic());
}