【笔记】机器学习 - 李宏毅 - 8 - Backpropagation

反向传播

反向传播主要用到是链式法则。

概念：
损失函数Loss Function是定义在单个训练样本上的，也就是一个样本的误差。
代价函数Cost Function是定义在整个训练集上的，也就是所有样本误差的总和的平均。有没有这个平均不会影响最后的参数求解结果。
总体损失函数Total Loss Function是定义在整个训练集上的，所有误差的总和，反向传播需要最小化的值。

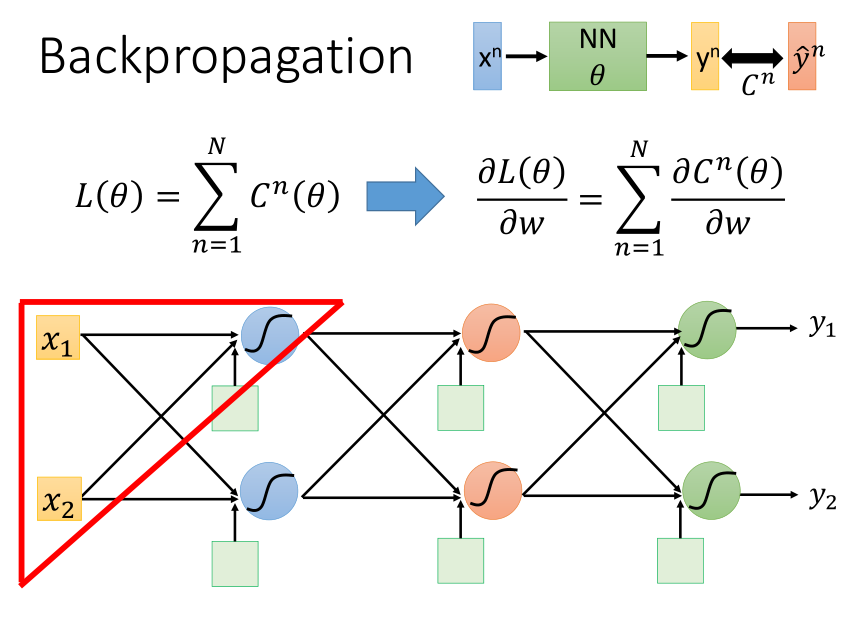
取一个神经元分析：

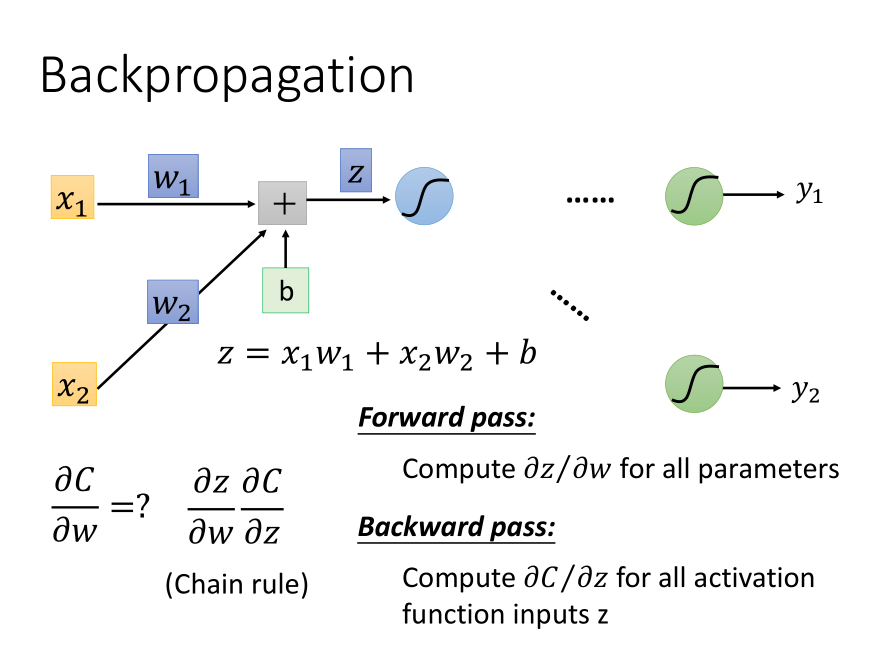
计算梯度分为两部分：
forward pass、backward pass

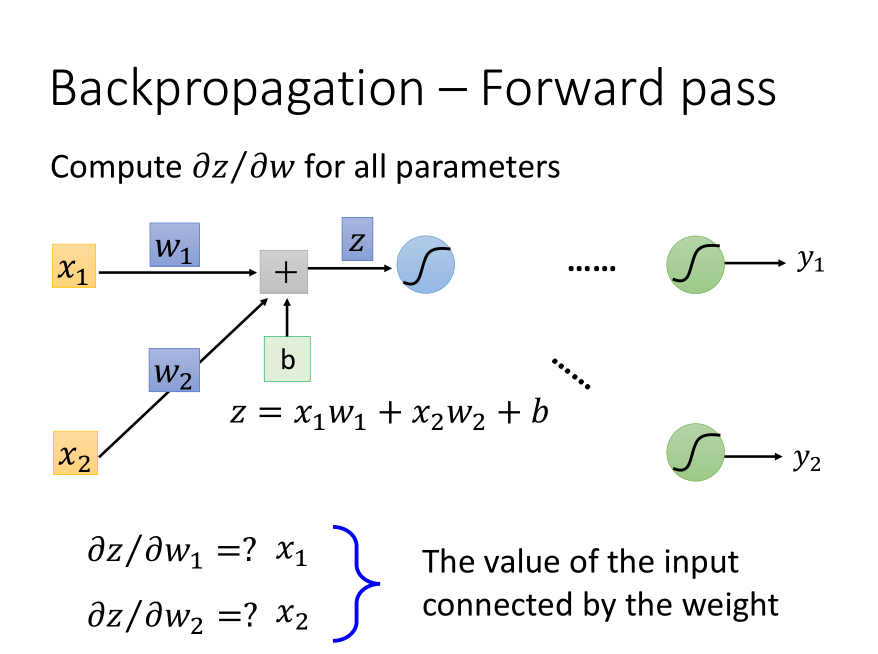
Forward Pass
求出的偏微分的值就是输入x的值，很好计算。

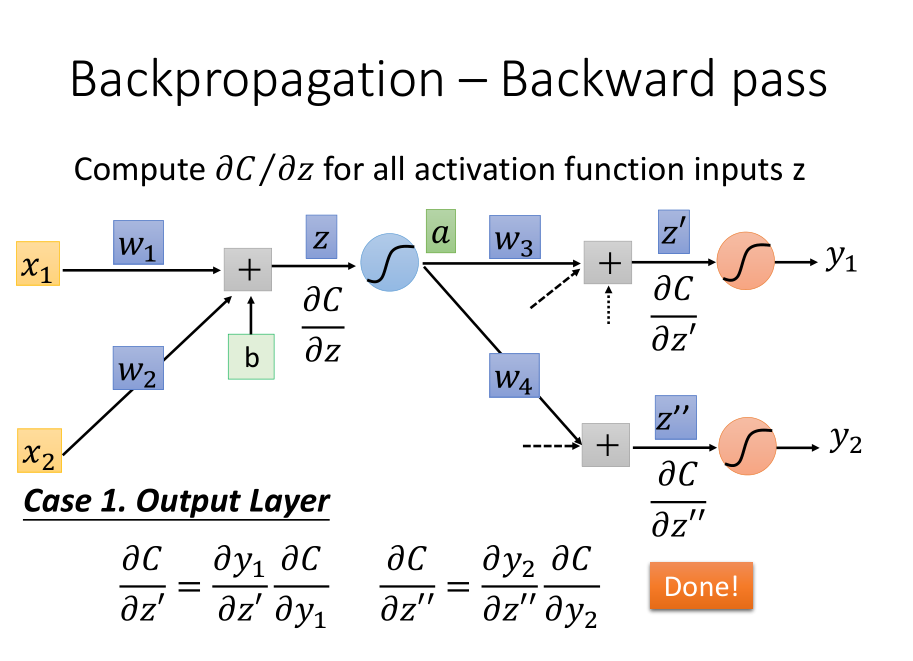
Backward Pass

激活函数是\(sigmoid\)的话，导数如图

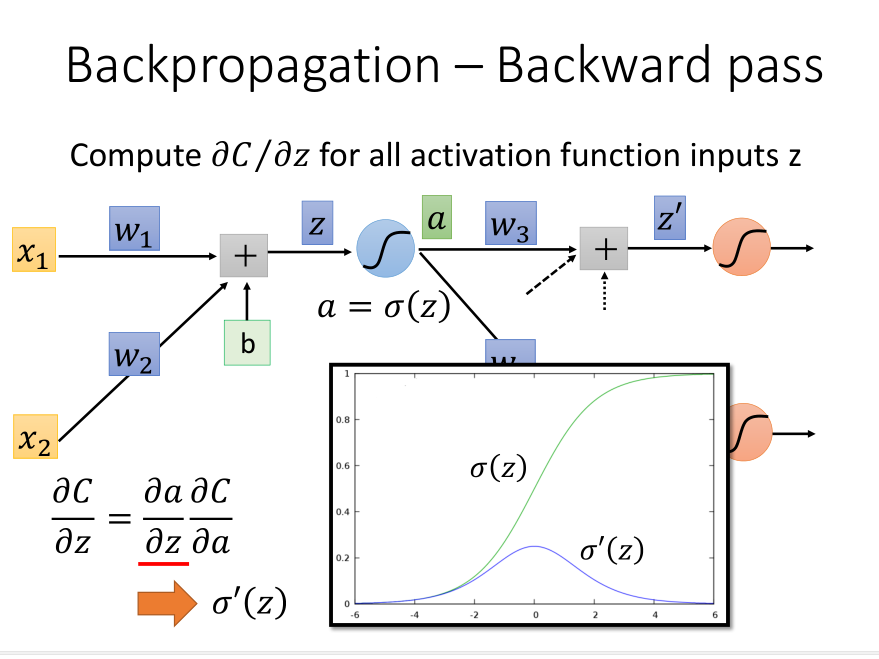
用链式法则计算
其中\({\sigma}'(z)\)是常数，因为\(z\)在向前传播的时候就已经确定了

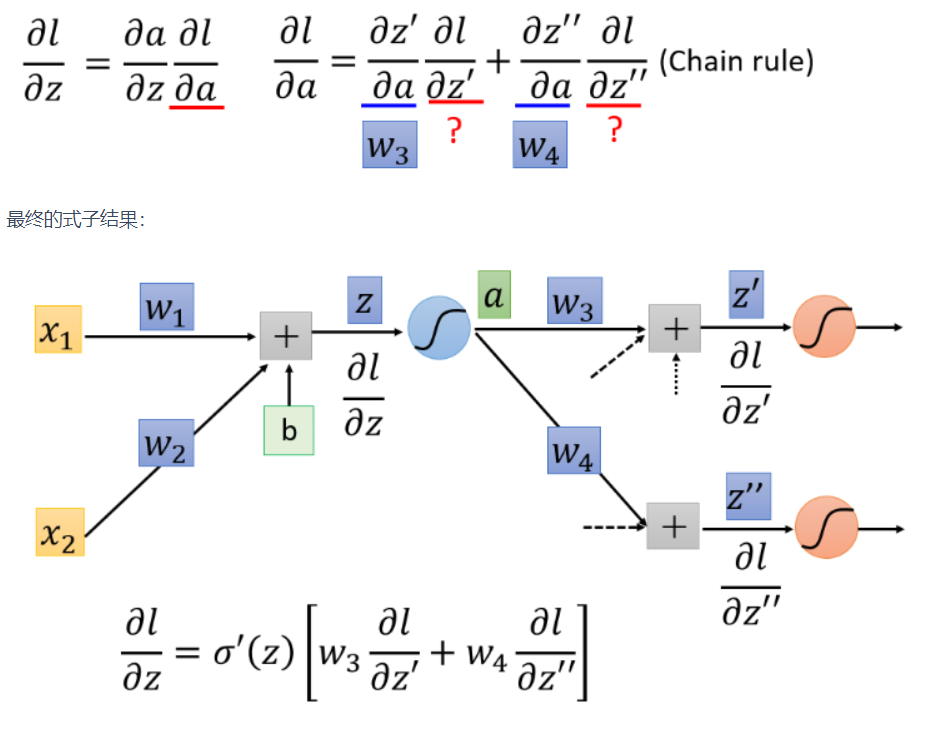
一直迭代计算到最后的输出层结束，然后结果逐层返回。

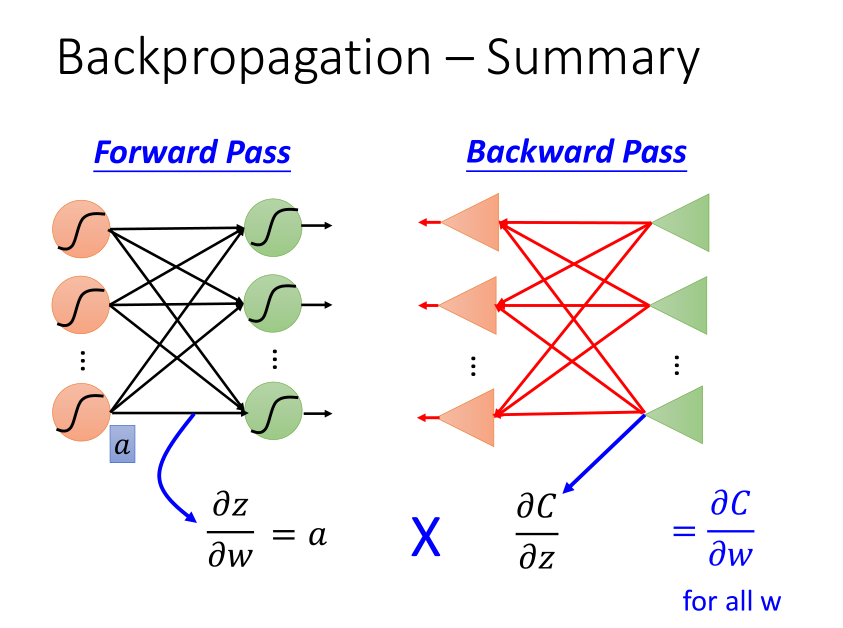
前向和后向：