纪中21日T3 2118. 【2016-12-30普及组模拟】最大公约数

纪中21日T3 2118. 最大公约数

(File IO): input:gcd.in output:gcd.out

时间限制: 1000 ms  空间限制: 262144 KB  具体限制

Goto ProblemSet

题目描述

给出两个正整数A，B，求它们的最大公约数。

输入

第一行一个正整数A。
第二行一个正整数B。

输出

在第一行输出一个整数，表示A，B的最大公约数。

样例输入

18
24 

样例输出

6 

数据范围限制

在40%的数据中，1 ≤ A，B ≤ 10^6
在60%的数据中，1 ≤ A，B ≤ 10^18
在80%的数据中，1 ≤ A，B ≤ 10^100
在100%的数据中，1 ≤ A，B ≤ 10^1000

Solution

Algorithm1

正常的gcd（a，b）=gcd（b，a%b）；

开unsigned long long可得六十分（应该不会超时）

Code1

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
using namespace std;
unsigned long long gcd(unsigned long long a,unsigned long long b)
{
    return b==?a:gcd(b,a%b);
}
unsigned long long a,b;
int main()
{
    cin>>a>>b;
    cout<<gcd(a,b);
     return ;
}

Attention1

函数也要开ULL（缩写）

别把“%”写成“-”，否则在相减前要先使得a>b

而且那样就变成更相减损法了

Algorithm2

gcd二进制法

先看看a，b是不是2的倍数

如果都是，gcd（a，b）=2*gcd（a/2，b/2）；

如果a是，gcd（a，b）=gcd（a/2，b）；

如果b是，gcd（a，b）=gcd（a，b/2）；

如果都不是，gcd（a，b）=gcd（b，a%b）

最后一条=gcd（b，a-b）也可以

（为后面的高精度做铺垫）

Code2

 #include<iostream>
 #include<iomanip>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<map>
 #include<set>
 #include<queue>
 #include<vector>
 #define IL inline
 using namespace std;
 IL unsigned long long gcdbin(unsigned long long a,unsigned long long b)
 {
     if(!b) return a;
     if(!(a|)&&!(b|)) return *gcdbin(a>>,b>>);
     if(!(a|)&&(b&)) return gcdbin(a>>,b);
     if((a&)&&!(b|)) return gcdbin(a,b>>);
     return gcdbin(b,a%b);
 }
 unsigned long long a,b;
 int main()
 {
     freopen("rand_gcd.txt","r",stdin);
     cin>>a>>b;
     cout<<gcdbin(a,b);
      return ;
 }

Code2

Algorithm3

不压位的高精度

高精度求余数很麻烦（按位求会比较快）

套用更相减损法

同时特判：如果a，b小于19位，依然采用二进制的辗转相除。

Code3

在GMOJ上……

Code3

由于是普通的更相减损，一旦数位超过20使用高精，速度就会很慢很慢很慢……

60分~80分不等

Algorithm4

高精压位

核心算法与Algorithm3相同

Code4

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
using namespace std;
const int L=;
int a[L],b[L],t[L];
int times=;
string stra,strb;
bool fail;
IL bool cmp()
{
    for(int i=L-;i>=;i--)
    {
        if(a[i]>b[i]) return ;
        if(a[i]<b[i]) return ;
    }
    return ;
}
IL void minus()
{

}
IL void diva()
{
    for(int i=L-;i>=;i--)
    {
        if(a[i]&) a[i-]+=;
        a[i]>>=;
    }
}
IL void divb()
{
    for(int i=L-;i>=;i--)
    {
        if(b[i]&) b[i-]+=;
        b[i]>>=;
    }
}
IL void div2()
{
    diva();
    divb();
}
int main()
{
//    freopen("gcd.in","r",stdin);
//    freopen("gcd.out","w",srdout);
    cin>>stra>>strb;
    for(unsigned int i=;i<stra.size();i++)
        a[i]=stra[stra.size()-i-];
    for(unsigned int i=;i<strb.size();i++)
        b[i]=strb[strb.size()-i-];
    do{
        if(!(a[]|)&&!(b[]|)){
            times*=;
            div2();
            continue;
        }
        if(!(a[]|)&&(b[]&))
        {
            diva();
            continue;
        }
        if((a&)&&!(b|))
        {
            divb();
            continue;
        }

        fail=;
        for(int i=;i<L;i++)
        {
            if(a[i]&&b[i])//会不会出现0与非0交错出现呢？概率是(1/10)^L吧……
            {
                fail=;
                break;
            }
        }
    }while(fail);
    bool zeroa;//为了避免交换，不能确定那个是0
    for(int i=;i<L;i++)
    {
        if(a[i]){
            zeroa=;
            break;
        }
        if(b[i]){
            zeroa=;
            break;
        }
    }
    bool flag=;
    if(zeroa)
    for(int i=;i<L;i++)
    {
        a[i]*=times;
        a[i+]+=(a[i]>>)+(a[i]>>);
        a[i]%=;
    }
    else
    for(int i=;i<L;i++)
    {
        b[i]*=times;
        b[i+]+=(b[i]>>)+(b[i]>>);
        b[i]%=;
    }
    if(zeroa)
    for(int i=L-;i>=;i--)
    {
        if(a[i]) flag=;
        if(flag) cout<<a[i];
    }
    else
    for(int i=L-;i>=;i--)
    {
        if(b[i]) flag=;
        if(flag) cout<<b[i];
    }

     return ;
}

Code4

Algorithm5

通过下面（最下面）的对拍发现，四种算法中，二进更相比普通更相更快（不是只有0.3毫秒么？）

高精（可以不压位）二进制更相减损术也不是很难打（而且判断也很快）

Algorithm6

之前是苦于没有时间打高精，终于在今天（2019-11-05 现在是00:17:29），我无意中点开了这篇题解，将我的高精度（甚至都没有压位）的模板稍作修改后边送上了“断头台”……

哈哈哈！

惊到我了！

Code6

由于是模板，所以代码较长。

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 using namespace std;

 bool insigma(char ch){
     return ch=='-'||(''<=ch&&ch<='');
 }

 const int maxn = ;
 struct number{
     int num[maxn];
     int len;
     bool fu;

     number(){//初始化
         len=fu=;
         memset(num,,sizeof(num));
     }

     int updata_len(){//更新长度
         for(int i=maxn-;i>=;i--) if(num[i]) return len=i+;
         return len=;
     }

     //    /*
     number operator= (int x){//隐式转换
         fu=(x<);
         num[]=abs(x);
         if(x>) carry_bit();
         if(x<-) back_space();
         return *this;
     }
 //    */
     /*
     number (int x){//有bug的构造函数 暂时用重载=替代
         fu=(x<0);
         num[0]=abs(x);
         if(x>9) carry_bit();
         if(x<-9) back_space();
     }
     */

     void input(){
 //        /*
         string a;
         cin>>a;
         if(a[]=='-'){
             fu=;
             len=a.size()-;
             for(unsigned int i=;i<a.size()-;i++) num[i]=a[a.size()-i-]-'';
         }
         else{
             len=a.size();
             for(unsigned int i=;i<a.size();i++)    num[i]=a[a.size()-i-]-'';
         }

 //        */
         /*
         len=0;
         char ch;
         while(!insigma(ch=getchar()));
         if(ch=='-')
             fu=true;
         else
             num[len++]=ch-'0';
         while(isdigit(ch=getchar())){
             num[len++]=ch-'0';
         }
         int t;
         for(int i=0;i<len;i++)
         {
             t=num[i];
             num[i]=num[len-i-1];
             num[len-i-1]=t;
         }
         */
     }

     void output(){
         if(fu) cout<<"-";
         bool flag=;
         for(int i=len;i>;i--){
             if(num[i]) flag=;
             if(num[i]>) carry_bit();
             if(flag) putchar(num[i]+'');//putchar加速
         }
         putchar(num[]+'');
     }

     friend istream & operator>> (istream &in, number &obj);
     friend ostream & operator<< (ostream &out, number &obj);

     int compare(number x){//2=    1> 0<
         if(fu^x.fu){
             if(fu) return ;
             else return ;
         }
         for(int i=max(len,x.len);i>=;i--)
         {
             if(num[i]>x.num[i]) return !fu;//大于 (1)
             if(num[i]<x.num[i]) return fu;//小于 (0)
         }
         return ;//相等
     }

     //利用compare()重载比较运算符 

     bool operator> (number x){
         return (compare(x)==);
     } 

     bool operator< (number x){
         return (compare(x)==);
     }

     bool operator>= (number x){
         return !(*this<x);
     }

     bool operator<= (number x){
         return !(*this>x);
     }

     bool operator== (number x){
         return compare(x)==;
     }

     bool operator!= (number x){
         return compare(x)!=;
     }

     number operator++ (){
         num[]++;
         if(num[]>) carry_bit();
         return *this;
     }

     number operator++ (int){
         number save=*this;
         ++*this;
         return save;
     }

     number operator-- (){
         num[]--;
         if(num[]<) back_space();
         return *this;
     }

     number operator-- (int){
         number save=*this;
         num[]--;
         if(num[]<) back_space();
         return save;
     }

     bool judge_zero(){
         for(int i=maxn-;i>=;i--)
             if(num[i]) return ;
         return ;
     }

     bool judge_non_zero(){
         return !judge_zero();
     }

     bool convert_bool(){
         return !judge_zero();
     }

     bool even(){
         if(num[]%) return ;
         return ;
     }

     bool odd(){
         if(num[]%) return ;
         return ;
     }

     void carry_bit(){
         for(int i=;i<maxn;i++){
             num[i+]+=num[i]/;
             num[i]%=;
         }
         updata_len();
     }

     void back_space(){
         for(int i=;i<maxn;i++){
             while(num[i]<) num[i]+=,num[i+]--;
         }
     }

     number operator+ (int x){
         number newness=*this;
         newness.num[]+=x;
         if(newness.num[]>) newness.carry_bit();
         return newness;
     }

     number operator+ (number x){
         number res=x;
         for(int i=;i<maxn;i++)
         {
             res.num[i]+=num[i];
         }
         res.carry_bit();
         return res;
     }

     number operator+= (int x){
         *this=(*this+x);
         return *this;
     }

     number operator+= (number x){
         *this=*this+x;
         return *this;
     }

     number operator- (number x){
         number i,j;
         if(compare(x)) {i=*this,j=x;}
         else {i=x,j=*this;}
         for(int t=;t<maxn;t++)
         {
             i.num[t]-=j.num[t];
         }
         i.back_space();
         return i;
     }

     number operator-= (number x){
         *this=*this-x;
         return *this;
     }

     number operator* (number x){
         number sum;
         sum.fu=fu^x.fu;
         for(int i=;i<updata_len();i++)
         for(int j=;j<x.updata_len();j++)
         {
             if(i+j>maxn-) continue;
             sum.num[i+j]+=num[i]*x.num[j];
         }
         sum.carry_bit();
         return sum;
     }

     number operator*= (number x){
         return *this=*this*x;
     }

     number factor(){
         number ans,t;
         t.num[]=;
         ans.num[]=;
         for(;t<=*this;t.num[]+=,t.carry_bit())
             ans*=t;
         return ans;
     }

     number division2(){
         for(int i=maxn-;i>=;i--){
             if(num[i]&&&i!=) num[i-]+=;
             num[i]>>=;
         }
         return *this;
     }
 };

 istream & operator>> (istream &in, number &obj)
 {
     string a;
     in>>a;
     if(a[]=='-'){
         obj.fu=;
         obj.len=a.size()-;
         for(unsigned int i=;i<a.size()-;i++) obj.num[i]=a[a.size()-i-]-'';
     }
     else{
         obj.len=a.size();
         for(unsigned int i=;i<a.size();i++) obj.num[i]=a[a.size()-i-]-'';
     }
     if (!in) obj = number();
     return in;
 }

 ostream & operator<< (ostream &out, number &obj)
 {
     if(obj.fu) cout<<"-";
         bool flag=;
         for(int i=obj.len;i>;i--){
             if(obj.num[i]) flag=;
             if(obj.num[i]>) obj.carry_bit();
             if(flag) out<<obj.num[i];
         }
         out<<obj.num[];
     return out;
 }

 number gcd_rec(number a,number b){
     if(b.judge_zero()) return a;
     return gcd_rec(b,a-b);
 }

 number gcd(number a,number b){
     if(a.judge_zero()) return a;
     number t;
     for(;;t=b,b=a-b,a=t)
         if(b.judge_zero()) return a;
     return a;
 }

 number power(number a,number n){
     number zero;
     number c;c=;
     for(;n>zero;n.division2(),a*=a) if(n.odd()) c*=a;
     return c;
 }

 int main()
 {
     freopen("gcd.in","r",stdin);
     freopen("gcd.out","w",stdout);
     number a,b,c;
     cin>>a>>b;
     c=gcd(a,b);
     cout<<c;
     return ;
 }

Impression

如果你有兴趣……

#pragma GCC optimize(2)
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
using namespace std;
unsigned long long gcd(unsigned long long a,unsigned long long b)
{
    return b==?a:gcd(b,a%b);
}
unsigned long long a,b;
int main()
{
    freopen("rand_gcd.txt","r",stdin);
    cin>>a>>b;
    cout<<gcd(a,b);
     return ;
}

gcd.cpp

#pragma GCC optimize(2)
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
using namespace std;
unsigned long long gx(unsigned long long a,unsigned long long b)
{
    if(a<b) swap(a,b);
    return b==?a:gx(b,a-b);
}
unsigned long long a,b;
int main()
{
    freopen("rand_gcd.txt","r",stdin);
    cin>>a>>b;
    cout<<gx(a,b);
     return ;
}

gx.cpp

#pragma GCC optimize(2)
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
using namespace std;
IL unsigned long long gcdbin(unsigned long long a,unsigned long long b)
{
    if(!b) return a;
    if(!(a|)&&!(b|)) return *gcdbin(a>>,b>>);
    if(!(a|)&&(b&)) return gcdbin(a>>,b);
    if((a&)&&!(b|)) return gcdbin(a,b>>);
    return gcdbin(b,a%b);
}
unsigned long long a,b;
int main()
{
    freopen("rand_gcd.txt","r",stdin);
    cin>>a>>b;
    cout<<gcdbin(a,b);
     return ;
}

gcdbin

#pragma GCC optimize(2)
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
using namespace std;
IL unsigned long long gxbin(unsigned long long a,unsigned long long b)
{
    if(!b) return a;
    if(!(a|)&&!(b|)) return *gxbin(a>>,b>>);
    if(!(a|)&&(b&)) return gxbin(a>>,b);
    if((a&)&&!(b|)) return gxbin(a,b>>);
    if(a<b) swap(a,b);
    return gxbin(b,a%b);
}
unsigned long long a,b;
int main()
{
    freopen("rand_gcd.txt","r",stdin);
    cin>>a>>b;
    cout<<gxbin(a,b);
     return ;
}

gxbin.cpp

#pragma GCC optimize(2)
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<windows.h>
#include<ctime>
#define IL inline
using namespace std;
int main()
{
    freopen("rand_gcd.txt","w",stdout);
    srand(time(NULL));
    cout<<(unsigned long long)rand()*rand()*rand()<<endl;
    cout<<(unsigned long long)rand()*rand()*rand()<<endl;
     return ;
}

rand_gcd.cpp

#pragma GCC optimize(2)
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<ctime>
#define IL inline
using namespace std;
int avg[];
int times;
int main()
{
    system("random_gcd.exe");
    int s1=clock();
    system("gcd.exe");
    int s2=clock();
    system("gcdbin.exe");
    int s3=clock();
    system("gx.exe");
    int s4=clock();
    system("gxbin.exe");
    int e=clock();
//    cout<<"\n辗转相除："<<s2-s1<<"ms\n";
//    cout<<"二进辗转："<<s3-s2<<"ms\n";
//    cout<<"更相减损："<<s4-s3<<"ms\n";
//    cout<<"二进更相："<<e-s4<<"ms\n";
    avg[]+=s2-s1;
    avg[]+=s3-s2;
    avg[]+=s4-s3;
    avg[]+=e-s4;
    times++;
    if(times>=)
    {
        system("cls");
        cout<<"总计"<<times<<"组数据\n";
        cout<<"平均用时：\n";
        cout<<"辗转相除："<<avg[]/(times*1.0)<<"ms\n";
        cout<<"二进辗转："<<avg[]/(times*1.0)<<"ms\n";
        cout<<"更相减损："<<avg[]/(times*1.0)<<"ms\n";
        cout<<"二进更相："<<avg[]/(times*1.0)<<"ms\n";
        return ;
    }
    main();
     return ;
}

gcd对拍.cpp

1000组数据运算结果如下

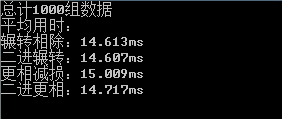
End